堆排序详解

如有错误，感谢不吝赐教、交流

算法原理

堆

堆是一个数组，可以被看成一个近似的完全二叉树，树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且是从左向右填充。
这里我们为了是数组中节点具有以下性质：第i个节点的父节点为(i)/2，左孩子节点为2i, 右孩子节点为2i + 1，故对于长度为n个元素的堆，使用n+1长度的数组，第0号位置不存入堆元素值。

返回节点i的父节点：

public static int parent(int i) {
        return i >> 1;  // 使用移位运算比除法快
    }

返回左孩子节点

public static int left(int i) {
        return i << 1;
    }

返回右孩子节点

 public static int right(int i) {
        return (i << 1) + 1;
    }

构建如图所示：注意数组下标是从1开始，即0号位置没有使用

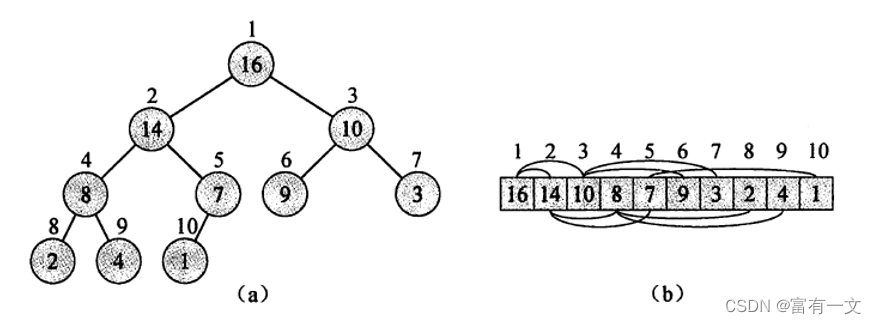
大根堆

除了根节点以外的所有节点，都要满足A[parent[i]] >= A[i]，即对于一个节点，它的值大于所有孩子节点的值

构建大根堆

维持大根堆的性质：如果左右孩子的值大于自己，就交换，否则不变

public static void maxHeapify(int a[], int i, int heapSize) {
        int l = left(i);
        int r= right(i);

        int largest;
        if (l <= heapSize && a[l] > a[i]) {
            largest = l;
        } else {
            largest = i;
        }
        if (r <= heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            exchange(a, largest, i);
            maxHeapify(a, largest, heapSize);
        }

    }

交换方法：

private static void exchange(int[] a, int largest, int i) {
        int temp = a[i];
        a[i] = a[largest];
        a[largest] = temp;
    }

建立大根堆：

public static void buildMaxHeap(int a[]) {
        int length = a.length - 1;
        // 大于length / 2位置的节点都是叶子节点
        for (int i = length / 2; i >= 1; i--) {
            maxHeapify(a, i, length);
        }
    }

堆排序的主入口：

public static void heapSort(int a[]) {
        buildMaxHeap(a);

        for (int j = a.length - 1; j >= 2; j--) {
            exchange(a, 1, j);
            maxHeapify(a, 1, j - 1);
        }
    }

小根堆

除了根节点以外的所有节点，都要满足A[parent[i]] <= A[i]，即对于一个节点，它的值小于所有孩子节点的值。
小根堆的使用方法与大根堆是一样的。

Java实现完整代码

java实现大根堆排序的完整代码：

public class HeapSort {
    // 返回节点i的父节点
    public static int parent(int i) {
        return i >> 1;
    }
    // 返回左孩子节点
    public static int left(int i) {
        return i << 1;
    }
    // 返回右孩子节点
    public static int right(int i) {
        return (i << 1) + 1;
    }

    public static void maxHeapify(int a[], int i, int heapSize) {
        int l = left(i);
        int r= right(i);

        int largest;
        if (l <= heapSize && a[l] > a[i]) {
            largest = l;
        } else {
            largest = i;
        }
        if (r <= heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            exchange(a, largest, i);
            maxHeapify(a, largest, heapSize);
        }

    }
    // 交换largest和i节点对应位置的值
    private static void exchange(int[] a, int largest, int i) {
        int temp = a[i];
        a[i] = a[largest];
        a[largest] = temp;
    }

    // 建立大根堆
    public static void buildMaxHeap(int a[]) {
        int length = a.length - 1;
        // 大于length / 2位置的节点都是叶子节点
        for (int i = length / 2; i >= 1; i--) {
            maxHeapify(a, i, length);
        }
    }

    // 堆排序主入口
    public static void heapSort(int a[]) {
        buildMaxHeap(a);

        for (int j = a.length - 1; j >= 2; j--) {
            exchange(a, 1, j);
            maxHeapify(a, 1, j - 1);
        }
    }

    public static void main(String[] args) {
        // 多申请一个是第0个位置不用，是的数组满足第i个位置对应的父节点为i/2，左孩子为2i，右孩子为2i + 1
        int arr [] = new int[]{0, 1, 5, 7, 3, 4, 10, 9, 8, 6};
        heapSort(arr);
        for (int a :
                arr) {
            System.out.print(a + " ");
        }
    }

}

总结

堆排序的时间复杂度是O(logn)，任何时候都只需要常数个额外的元素空间存储临时数据。
适用于大量数据下需要取出前100最大，或者前100最小等一些场景。

ps:面试的时候，自己居然记不住自己写过的博客，这里给出一个Java版本的简单实现方式，相比上面的更加简单

import java.util.*;
public class Main {
    public static void main(String[] args) {
        int arr [] = new int[]{0, 2, 4, 3, 8, 6, 9};
        int l = arr.length;
        for (int i = 0; i < arr.length; i++) {
            fun(arr, l);
            if(l > 1) {
                int temp = arr[1];
                arr[1] = arr[l-1];
                arr[l-1] = temp;
            }
            System.out.println(arr[l-1]);
            l--;
        }
    }
    public static void fun(int arr [], int l) {
        int tmp [] = new int[l];
        for(int i = 1; i<l; i++) {
            tmp[i] = arr[i];
        }
        for(int i = tmp.length - 1; i > 1; i--) {
            if(tmp[i] > tmp[i/2]) {
                int temp = tmp[i];
                tmp[i] = tmp[i/2];
                tmp[i/2] = temp;
            }
        }
        for(int i = 1; i < l; i++) {
            arr[i] = tmp[i];
        }
    }
}

ps:计划每日更新一篇博客，今日2023-04-24，日更第八天，昨日更新：
冒泡排序
选择排序
插入排序
归并排序