背包问题

题目:小明去旅游需要带上一些物品，有5中物品选择，每种物品的体积，重量，数量，价值分别如下：

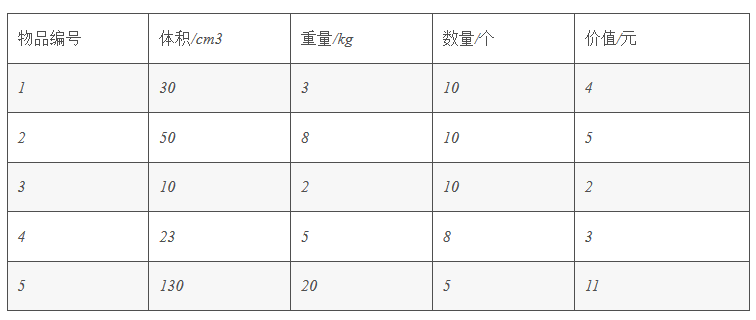
现在限制总的体积最多为500 cm3，总的重量最多为100 KG，请问小明能带上的物品的最大总价值是多少？

#include<stdio.h>
#include<string.h>
#define maxn 6
int v[maxn],w[maxn],c[maxn],t[maxn];
int f[6][501][101];
int s[6][501][101];
int main()
{
    int i,num,maxx,maxy;
    int n,x,y,k;
    scanf("%d",&num);
    for(i=1;i<=num;i++)
    {
        scanf("%d,%d,%d,%d",&v[i],&w[i],&c[i],&t[i]);
    }
    scanf("%d,%d",&maxx,&maxy);

    //物品种类为num
    for(n=1;n<=num;n++)
        //设置可接受的体积
        for(x=1;x<=maxx;x++)
        //设置可接受的重量
            for(y=1;y<=maxy;y++)
            {
                //设置对于物品n最多可以容纳多少个，这是通过体积和重量的双重限制而得出的
                int maxi=c[n];
                if(x/v[n]<maxi)maxi=x/v[n];
                if(y/w[n]<maxi)maxi=y/w[n];
                for(i=0;i<=maxi;i++)
                {//如果当前的结果可以使背包有更高的价值，那么添加上去
                    if(f[n][x][y]<f[n-1][x-i*v[n]][y-i*w[n]]+i*t[n]){
                        f[n][x][y]=f[n-1][x-i*v[n]][y-i*w[n]]+i*t[n];
                        s[n][x][y]=i;
                    }

                }
            }
    int result=0;
    int xx=0,yy=0;
    //获取最大价值
    for(x=0;x<=maxx;x++)
    {
        for(y=0;y<=maxy;y++)
            if(f[num][x][y]>result)
                {
                    result=f[num][x][y];
                    xx=x;
                    yy=y;
                }
    }
    //输出每种物品的装包数量
    for(k=num;k>=1;k--)
    {
        int temp=s[k][xx][yy];
        printf("物品%d的数量为:%d\n",k,s[k][xx][yy]);
        xx-=temp*v[k];
        yy-=temp*w[k];
    }
    printf("最大价值为%d\n",f[num][maxx][maxy]);
    return 0;
}