浅谈算法--时间复杂度和空间复杂度

最近学习了python版数据结构和算法，做一些必要的笔记，一来是对自己学习的知识的巩固，二来对有同样问题的人有参考作用

---

---

一 时间复杂度

1、基本概念

（1）时间频度：一个算法执行所耗费的时间，也就是一个算法中的语句执行次数称为语句频度或时间频度，记为T(n)。

（2）空间复杂度：一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

2、求解时间复杂度的步骤

（1）找到执行次数最多的语句

（2）语句执行语句的数量级

（3）用O表示结果

第三步的转化f(n)具体操作：

• 用常数1取代运行时间中的所有加法常数

• 在修改后的运行次数函数中，只保留最高阶项

• 如果最高阶项存在且不是1，那么我们就去除于这个项相乘的常数。比如3n ^2 我们取 n^2

最后就可以得到你们想要的结果了。

3、常见例子

(1) 常数阶

public class TS {
	public static void main(String[] args) {
		System.out.println("111");
		System.out.println("111");
		System.out.println("111");
		System.out.println("111");
		System.out.println("111");
		System.out.println("111");
		System.out.println("111");
		System.out.println("111");
	}
}

显然，T(n) = 8，但是 f(n) = 1，所以时间复杂度为: O(1)。

（2） 线性阶

public class TS {
	public static void main(String[] args) {
		int sum = 0;
		for(int i=1;i<=100;i++) {
			sum = sum + 0;
			sum = sum + i;
		}
	}
}

问题规模n = 100，T(n) = 2n，f(n) = n，所以时间复杂度为：O(n)。

（3） 平方阶

public class TS {
	public static void main(String[] args) {
		int sum = 0;
		for(int i=1;i<=100;i++) {
			for(int j=1;j<=100;j++)
				sum = sum + i;
		}
	}
}

问题规模n = 100，T(n) = n^2，f(n) = n^2，所以时间复杂度为O(n ^2)

平方阶的另外一个例子：

public class TS {
	public static void main(String[] args) {
		int sum = 0;
		for(int i=1;i<=100;i++) {
			for(int j=i;j<=100;j++)
				sum = sum + i;
		}
	}
}

当i=1的时候执行n次，当n=2的时候执行（n-1）次，…

求和易得：n+n*(n-1)/2整理一下就是n*(n+1)/2然后我们将其展开可以得到n^2/2+n/2。

根据我们的步骤走，保留最高次项，去掉相乘的常数就可以得到时间复杂度为：O(n^2)。

（4）对数阶

public class TS {
	public static void main(String[] args) {
		int i=1;
		int n= 100;
		while(i<n) {
			i = i*2;
		}	
}

2^x = n，所以时间复杂度为O(log2n)。

4、常用的时间复杂度排序

O(1 ) < O(logn) < O(n) < O(n*logn) < O(n^2) < O(2^n) < O(n!) < O(n^n)

二 空间复杂度

1、基本概念
算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n) = O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数，也是一种“渐进表示法”，这些所需要的内存空间通常分为“固定空间内存”（包括基本程序代码、常数、变量等）和“变动空间内存”（随程序运行时而改变大小的使用空间）

通常，我们都是用“时间复杂度”来指运行时间的需求，是用“空间复杂度”指空间需求。

当直接要让我们求“复杂度”时，通常指的是时间复杂度。

2、计算方法

（1）忽略常数，用O(1)表示

（2）递归算法的空间复杂度=递归深度N*每次递归所要的辅助空间

（3）对于单线程来说，递归有运行时堆栈，求的是递归最深的那一次压栈所耗费的空间的个数，因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。

3、常见例子

（1）常数阶

a = 0
b = 0
print(a,b)

它的空间复杂度为 O(1)；

temp=0;
for(i=0;i<n;i++):
    temp = i

temp定义在循环外边，所以是1*O(1) 。

（2）线性阶

def fun(n):
    k = 10
    if n == k:
        return n
    else:
        return fun(++n)

递归实现，调用fun函数，每次都创建1个变量k。调用n次，空间复杂度 O(n)。

for(i=0;i<n;++):
  temp = i

变量的内存分配发生在定义的时候，因为temp的定义是循环里边，所以是n*O(1)。

三 常用算法的时间复杂度和空间复杂度

空间换时间是常见的操作。

---

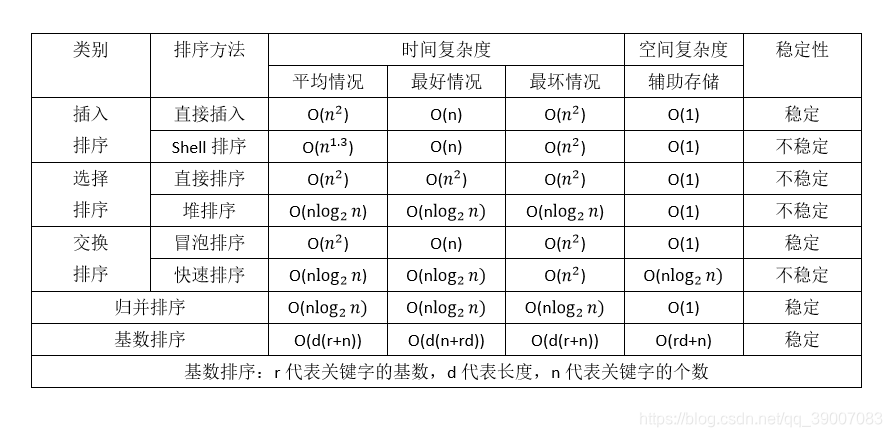
四 总结

如有错误恳请指正，如有侵权请联系我删除
参考文章: 算法的时间复杂度和空间复杂度-总结
                计算时间复杂度–（简单版）
                算法的时间复杂度和空间复杂度计算