看题:
输入正整数k,找到所有的正整数x≥y,使得1/k=1/x+1/y
样例输入:
2
12
样例输出:
2
1/2=1/6+1/3
1/2=1/4+1/4
8
1/12=1/156+1/13
1/12=1/84+1/14
1/12=1/60+1/15
1/12=1/48+1/16
1/12=1/36+1/18
1/12=1/30+1/20
1/12=1/28+1/21
1/12=1/24+1/24
分析一下题:
通过题目可以看出:找出所有有x,y,枚举完成了就行了!!!
哈哈,纯纯的枚举,即简单又暴力!!!
注意!!!
细节来了:
1/12=1/156+1/13 可以看出,x可以比y大很多。
推导———
因为:x≥y
所以:1/x≤1/y
因此 : 1/k-1/y≤1/y
即可推出:y≤2k。
这样,只需要在2k范围内枚举y,然后根据y尝试计算出x即可
计算x的步骤:
1/k=1/x+1/y
1/x=1/k-1/y
右边通分化简得
x=(k * y) / (y - k);
直接上代码:
import java.util.Scanner;
class Main {
public static void main(String[] args) {
int x, y;//变量count统计等式的个数
Scanner sc = new Scanner(System.in);
while(sc.hasNext()) {
int k = sc.nextInt();
int count = 0;
for(y = k+1;y <= 2 * k; y++){ //判断1/k=1/x+1/y等式的个数
x=(k * y) / (y - k); //注意!!!求解x公式
if(x * (y-k) == k * y){
System.out.printf("1/%d=1/%d+1/%d\n",k,x,y);
count++;
}
}
System.out.printf("%d\n",count);//输出满足条件的等式的个数
}
}
}
运行结果如图所示:
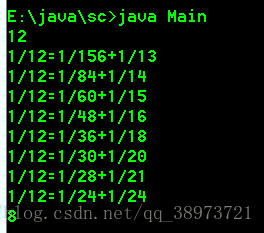




 本文介绍了一种利用枚举法解决特定分数方程的方法,并提供了完整的Java实现代码。该方法适用于寻找所有符合条件的正整数x和y,使得1/k=1/x+1/y成立。
本文介绍了一种利用枚举法解决特定分数方程的方法,并提供了完整的Java实现代码。该方法适用于寻找所有符合条件的正整数x和y,使得1/k=1/x+1/y成立。

















 1756
1756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










