OpenCV SIFT特征检测的原理及其实现步骤

本文架构

• SIFT简介
• SIFT算法的实质
• SIFT算法的特点
• SIFT算法可以解决哪些问题
• SIFT算法的实现步骤
• 尺度空间的获取–高斯模糊（必备知识）
• SIFT算法实现的第一步–尺度空间极值检测
• SIFT算法实现的第二步–关键点定位
• SIFT算法实现的第三步–关键点方向定位（方向确定）
• SIFT算法实现的第四步–关键点描述
• SIFT的缺点
• SIFT实现代码

---

SIFT简介

• SIFT（Scale-invariant feature transform）是一种电脑视觉的算法，用来侦测与描述影像中的局部性特征，并在空间尺度中寻找极值点，提取出特征在图像中的位置、尺度、以及旋转不变量。
• SIFT是基于物体上的一些局部外观的兴趣点进行检测与影像的大小和旋转无关，同时对于光线、噪声、微视角改变的容忍度也相当高，基于这些特点，很容易辨识图像中的物体而且少有误认。
• SIFT对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。（带着口罩进行人脸识别）
• SIFT应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。

---

SIFT算法的实质

• SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。
• SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等

---

SIFT算法的特点

1. 稳定性：SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度、视角变化、仿射变换、噪声变化保持不变性
2. 独特性：信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配
3. 多量性：即使少数的几个物体也可以产生大量的SIFT特征向量
4. 高速性：经优化的SIFT匹配算法甚至可以达到实时的要求
5. 可扩展性：可以很方便的与其他形式的特征向量进行联合。（比如对位置的限制、对于大小的限制）

---

SIFT算法可以解决那些问题

• 目标的旋转、缩放、平移（RST）
• 图像仿射/投影变换（视点viewpoint）
• 光照影响（illumination）
• 目标遮挡（occlusion）
• 杂物场景（clutter）
• 噪声

对于以上这些问题，虽然SIFI可以解决，但还是需要考虑外界的干扰因素的（影响识别的准确率）

---

SIFT算法的实现步骤

1. 尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。
2. 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。
3. 方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。
4. 关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

---

尺度空间的获取–高斯模糊

SIFT算法是在不同的尺度空间上查找关键点，而尺度空间的获取需要使用高斯模糊来实现。

可能你会疑惑，什么是尺度空间呢？( ´･ω･)ﾉ(._.`)
尺度空间的大体意思是：多个尺度下观察目标，然后加以综合的分析和理解（可能还有点抽象）
举个例子：比如放学去食堂，此时食堂就是你的观察目标，在你离食堂越近的时候，你看食堂可能会更清晰（这就是不同尺度下观察食堂），也就是说不同的尺度空间对于目标的观察是不同的（有点扯远了，哈哈）（到后面会详细的讲解什么是尺度空间~ 先了解个大概）

那什么又是高斯模糊呢？

高斯模糊可以理解为一种图像的滤波器，使用正态分布来计算模糊模板（记住就行哈），然后使用这个模板与原图进行卷积运算，从而达到模糊图像的目的（为什么SIFT要模糊图像，我稍后解答）

当然我们还需要了解N维空间的正态分布方程（方便理解~）:$G(r)=\frac{1}{(\sqrt{2\pi {\delta }^2}{)}^N}{e}^{-\frac{r^2}{2{\delta }^2}}$

• $\delta$是正态分布的标准差，$\delta$的值越大，图像越是模糊（平滑）
• $r$是模糊半径，就是指模板元素到模板中心的距离（有点抽象哈）

公式有点抽象，我们来举个例子。

有一个二维模板，他的大小是m*n，那么这个模板上的元素（x,y）对应的高斯计算公式是：$G(x,y)=\frac{1}{(\sqrt{2\pi {\delta }^2}{)}^N}{e}^{-\frac{(\frac{x-m}{2}{)}^2+(\frac{y-n}{2}{)}^2}{2{\delta }^2}}$

公式这回应该是了解如何使用了（记住公式就得了，咱不搞数学哈(^_−)☆）

有了公式，咱们再搞个可视化看看：

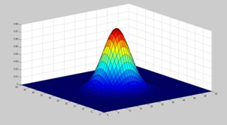
从图像中，我们不难看出在二维空间中，曲面的等高线是从中心开始呈正态分布的同心圆。（这个应该好理解）

我们在回归的卷积的问题，如果一个分布不为零的像素组成的卷积矩阵与原图形做变换，那么得到的结果会是什么呢？

首先，我们回归到卷积的原理上，如果进行卷积，每个像素的值都是周围相邻像素值得加权平均吧（此处无异议）

那么，原图像的像素的值就有了最大的高斯分布值，也就有了最大的权重

当然那些距离原图像像素远的像素值，权重也就是小的（可以理解吧）

那么以上的这波操作，会比其他类型的均衡模糊滤波器更高的保留边缘效果。
（读到这里，你可能会猜想一些事情，模糊图像和SIFT有什么关系呢(✪ω✪)，好像有答案啦~）

从理论上来说，如果图形中的每个点的分布都不为零，那可要计算整个图片了！！！！

不过，在实际应用中，计算高斯函数的离散近似的时候，往往将距离大于$3\delta$的像素（距离太远）都看作是不起作用的，通俗的说，就是不用计算（比如上面的那个图像，咱们掐尖计算即可）

通常，图像处理程序只需要计算$(6\delta +1)\ast (6\delta +1)$的矩阵就可以保证相关像素的影响（科学家研究的，记住就行啦~）

根据$\delta$的值，我们可以计算高斯模板矩阵的大小$(6\delta +1)\ast (6\delta +1)$，使用$G(x,y)=\frac{1}{(\sqrt{2\pi {\delta }^2}{)}^N}{e}^{-\frac{(\frac{x-m}{2}{)}^2+(\frac{y-n}{2}{)}^2}{2{\delta }^2}}$公式，我们可以计算高斯模板矩阵的值，并与原图像做卷积，这样就可以获得了原图像的平滑（高斯模糊）图像

为了确保模板矩阵中的元素在[0, 1]之间，需要将模板进行归一化处理，即可得5*5的高斯模板

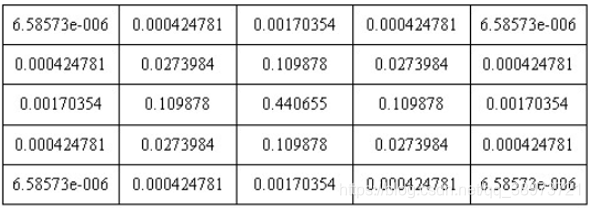
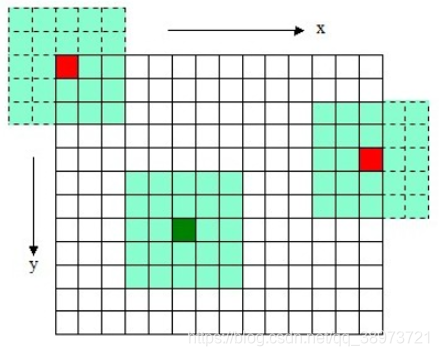
卷积示意图：

我们再来看看效果图~~

通过上面的图片，再次确认二维高斯模板实现了模糊图像的目的(｡-_-｡)

图b和图c 就是因为模板矩阵的关系，从而造成了边缘图像缺失（模糊了~）

$\delta$的值越大，缺失的像素也就越多，丢弃模板会造成黑边（图d）

当然，我们也不能忘记一点，$\delta$的值越大，咱的计算量也是成几何倍的增长！！！

怎么优化这个计算呢？我们再次引入高斯函数的可分离性~

高斯函数的可分离性是指：

用二维矩阵变换得到的效果也可以等同于在水平和竖直方向各做一次高斯矩阵变换
用公式来解释的话，就是由原来的$O(m\ast n\ast M\ast N)$转换成了$O(n\ast M\ast N)+O($