7.l滤波

最新推荐文章于 2025-04-01 06:26:13 发布

澜生Python笔谈

最新推荐文章于 2025-04-01 06:26:13 发布

阅读量341

点赞数

分类专栏： opencv 文章标签：卷积 opencv 计算机视觉边缘检测 cv

本文链接：https://blog.youkuaiyun.com/qq_38939991/article/details/109496256

版权

opencv 专栏收录该内容

11 篇文章

订阅专栏

学习视频可参见python+opencv3.3视频教学基础入门

今天写的是滤波

outline

均值滤波
中值滤波
自定义滤波
高斯滤波（模糊）

图像基础常识：

噪声

椒盐噪声（Salt & Pepper）：含有随机出现的黑白亮度值。（加了胡椒粉，很形象了）
- 盐=白色，椒=黑色
高斯噪声：含有亮度服从高斯或正态分布的噪声。高斯噪声是很多传感器噪声的模型，如摄像机的电子干扰噪声。

滤波器

线性滤波器
- 线性滤波器的原始数据与滤波结果是一种算术运算，即用加减乘除等运算实现，
- 如均值滤波器（模板内像素灰度值的平均值）、高斯滤波器（高斯加权平均值）等。
- 由于线性滤波器是算术运算，有固定的模板，因此滤波器的转移函数是可以确定并且是唯一的（转移函数即模板的傅里叶变换）。
非线性滤波
- 非线性滤波器的原始数据与滤波结果是一种逻辑关系，即用逻辑运算实现。
- 如最大值滤波器、最小值滤波器、中值滤波器等。
- 通过比较一定邻域内的灰度值大小来实现的，没有固定的模板，因而也就没有特定的转移函数（因为没有模板作傅里叶变换），另外，膨胀和腐蚀也是通过最大值、最小值滤波器实现的。

滤波、模糊等之间的关系

一张图明白易懂
滤波
- 对输入信号进行卷积处理的一个过程，其实滤波 = 卷积
- 卷积模板/掩膜的不同决定了不同的滤波方式，也因此产生了高通、低通、带通、带阻等基本的滤波方式。（高斯掩模最后要进行归一化处理，即映射到0-1的范围）
- 低通滤波：就是保留将信号中的低频部分，抑制高频部分。可用均值滤波，高斯滤波处理。
- 均值滤波：采用均值掩膜对输入信号进行卷积的滤波方式叫均值滤波。
- 高斯滤波：采用高斯掩膜对输入信号进行卷积的滤波方式叫高斯滤波；

1.均值滤波

均值滤波是低通滤波，线性滤波器，其输出为邻域模板内像素的平均值，用于图像的模糊和降噪。

def blur_demo(image):
    dst = cv.blur(image, (5,5))  # 卷积核为5x5，均值
    cv.imshow("blur",image)

均值滤波器使用滤波器窗口内的像素的平均灰度值代替图像中的像素值，这样的结果就是降低图像中的“尖锐”变化。这就造成，均值滤波器可以降低噪声的同时，也会模糊图像的边缘。

2.中值滤波

中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。
中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近的真实值，从而消除孤立的噪声点。

def memedianBlur(image):
    dst = cv.medianBlur(image, 5)  # 中值模糊，对椒盐噪声去噪较好
    cv.imshow("medianBlur",dst)

去除椒盐噪声较好。
中值滤波对脉冲噪声有良好的滤除作用，特别是在滤除噪声的同时，能够保护信号的边缘，使之不被模糊。这些优良特性是线性滤波方法所不具有的

3.自定义滤波

def custom_blur_demo(image):
    #自定义滤波器
    kernel = np.ones([5, 5], np.float32) / 25  # 卷积核核大小
    # filter2D(src, ddepth(图像深度，-1表示默认和src一样深度), kernel, dst=None, anchor=None(锚点，卷积核中心), delta=None, borderType=None)
    dst=cv.filter2D(image, -1, kernel=kernel)  # 二维滤波器
    cv.imshow("blur_demo", dst)

kernel = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]], np.float32)  # 锐化算子

- 可以观察到比原来更加立体
- 算子为奇数，总和为0，做边缘梯度，即边缘检测，总和为1，做增强
- 总和为0的算子：
- 测试用例：
- ```
kernel = np.array([[0,1,2], [-1, 0,1], [-2, -1,0]], np.float32)  # 锐化算子
```
- 结果：
- [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XLROQlgM-1604485791381)(https://gitee.com/guohui7/weixinpicture/raw/master/img/image-20201104180922566.png)]

4.高斯滤波（模糊）

高斯分布（正态分布）
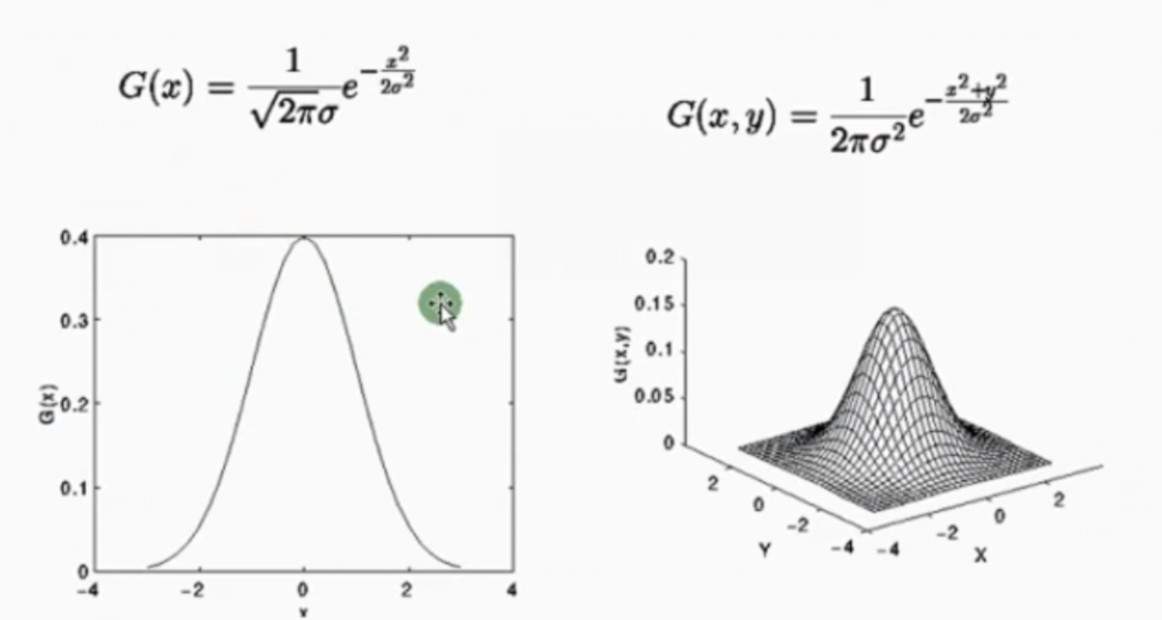
高斯滤波是最常用的图像去噪方法之一，它能很好地滤除掉图像中随机出现的高斯噪声

对原图加高斯噪声

#0-255范围
def clamp(pv):
    if pv > 255:
        return 255
    elif pv < 0:
        return 0
    else:
        return pv


def gaussian_noise(image):  # 加高斯噪声
    h, w, c = image.shape
    for row in range(h):
        for col in range(w):
            s = np.random.normal(0, 20, 3)  # normal(loc=0.0, scale=1.0, size=None),均值，标准差，大小

            b = image[row, col, 0]
            g = image[row, col, 1]
            r = image[row, col, 2]

            image[row, col, 0] = clamp(b + s[0])
            image[row, col, 1] = clamp(g + s[1])
            image[row, col, 2] = clamp(r + s[2])

    cv.imshow("gaussian_noise", image)

得到结果如下：

运用高斯滤波处理图像：

# GaussianBlur(src, ksize, sigmaX, dst=None, sigmaY=None, borderType=None)
    # ksize表示卷积核大小，sigmaX，Y表示x，y方向上的标准差，这两者只需一个即可，并且ksize为大于0的奇数
    dst = cv.GaussianBlur(src, (5, 5), 0)  # 高斯模糊，sigmaX与ksize一个为0
    cv.imshow("Gaussian blur", dst)