图算法: 最小生成树、最短路径、并查集、dfs、bfs

并查集

树型数据结构，处理Disjoint Sets的合并和查询

import java.util.Scanner;

public class FindMergeSet {
	static int n;
	static int m;
	static int[] pre = new int[10005];
	
	public static int find(int k){//寻找k的根结点
		if(pre[k] == k) return k;//判断该结点是否根节点：pre值是否是自身下标
		return pre[k] = find(pre[k]);//递归路径压缩
	}
	
	public static void merge (int a,int b){//合并集合
		int t1 = find(a);
		int t2 = find(b);
		if(t1 != t2)
			pre[t1] = t2;//把左边集合变成右边子集合
	}
	
	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		n = in.nextInt();
		m = in.nextInt();
		int x,y,z;
		
		for(int i = 1; i <= n;i++){
			pre[i] = i;//每个结点的父结点初始化为自己
		}
		
		for(int i = 1; i <= m;i++){
			x = in.nextInt();
			y = in.nextInt();
			z = in.nextInt();
			if(z == 1) //z==1时，执行合并操作
				merge(x,y);
			else{
				//判断根结点是否相同
				if(find(x) == find(y))
					System.out.println("在同一集合中");
				else
					System.out.println("不在同一集合中");
			}
		}
		
	}

}

 

 

MST----Kruskal算法

定义边结构->优先队列（读数据，按权值存边）或者  边结构实现comparable接口Arrays.sort(edges)

->初始化为独立树pre[i] = i

->定义寻找根节点find函数（递归和非递归）和合并集合merge函数（路径压缩）

->按权值从小到大取边

->不在同一棵树边顶点合并到一棵树（同一根节点）

->依据情况对边权值进行记录->直到有n-1条边或所有顶点在一棵树上

 

例题1：

思路：
Tmax=max(Th)表示Tmax由单层最大消耗时间max(Th)决定,
而max(Th)又由该深度权值最大的一条边max(th,j)决定，所以可以理解为Tmax​由最小生成树中最大边权值决定。

跑一遍最小生成树求出最大边权即可。 

import java.util.PriorityQueue;
import java.util.Scanner;

public class MSTDataCenter {
	static class Edge{
		int u,v,w;
	}
	
	static int[] pre;
	static Edge[] edges;
	
	static int find (int k){//寻找k的根节点
		if(pre[k] == k)
			return k;
		return pre[k] = find(pre[k]);
	}
	
	static void merge(int x,int y){//合并集合
		int v1 = find(x);
		int v2 = find(y);
		if(v1 != v2)
			pre[v1] = v2;//左边集合变成右边子集合
	}
	
	static void init(int[] pre){//初始化
		for(int i = 1; i < pre.length; i++){
			pre[i] = i;
		}
	}
	
	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		int vertexNum = in.nextInt();
		int edgeNum = in.nextInt();
		int root = in.nextInt();
		pre = new int[vertexNum + 1];
		edges = new Edge[edgeNum];
		
		PriorityQueue<Edge> graph = new PriorityQueue<>((v1,v2) ->v1.w - v2.w);
		for(int i = 0 ; i < edgeNum; i++){
			edges[i] = new Edge();//*!!!
			edges[i].u = in.nextInt();
			edges[i].v = in.nextInt();
			edges[i].w = in.nextInt();
			graph.add(edges[i]);
		}
		
		init(pre);
		
		int ans = 0, eNum = 0;
//		while(!graph.isEmpty()){
//			Edge e = graph.poll();
//			int fu = find(e.u);
//			int fv = find(e.v);
//			if(fu != fv){
//				pre[fu] = fv;
//				ans = Math.max(ans, e.w);
//				eNum++;
//				if(eNum == vertexNum - 1) break;
//			}
//		}
		while(!graph.isEmpty()){
			Edge e = graph.poll();
			merge(e.u,e.v);
			
			ans = Math.max(ans, e.w);
			
			eNum++;
			if(eNum == vertexNum - 1) break;
		}
		
		System.out.println(ans);
		
		in.close();
	}

}
/*两节点相连可互传数据，每个节点选择一条路径将数据发送到root节点，使得时间最少
 * 每个节点只能将数据传输给一个数据，但能接收多个不同节点的数据
 * 
 样例输入
4
5
1
1 2 3
1 3 4
1 4 5
2 3 8
3 4 2
样例输出--最优树结构流水线耗时Tmax
4
 */

例题2：

思路：为了让Start和End有路径，只需要按照kruskal算法从"最小路径"开始构造生成树，一旦发现Start和End有连接了，那么就表示已经构成满足条件的那个路径。由于路径已经排序好，那么此时所枚举“起点”和“满足条件之点”之差便是最大速度与最小速度之差。

import java.util.Arrays;

import java.util.PriorityQueue;
import java.util.Scanner;
/*
XX星有许多城市，城市之间通过一种奇怪的高速公路SARS进行交流，每条SARS都对行驶在上面的Flycar限制了固定的Speed，
同时XX星人对 Flycar的“舒适度”有特殊要求，即乘坐过程中最高速度与最低速度的差越小乘坐越舒服 ,(理解为SARS的限速要求，flycar必须瞬间提速/降速 ),
但XX星人对时间却没那么多要求。要你找出一条城市间的最舒适的路径。(SARS是双向的）。

输入包括多个测试实例，每个实例包括：
第一行有2个正整数n (1<n<=200)和m (m<=1000),表示有N个城市和M条SARS。
接下来的行是三个正整数StartCity,EndCity,speed,表示从表面上看StartCity到EndCity,限速为speedSARS。speed<=1000000
然后是一个正整数Q（Q<11),表示寻路的个数。
接下来Q行每行有2个正整数Start,End, 表示寻路的起终点。

每个寻路要求打印一行，仅输出一个非负整数表示最佳路线的舒适度最高速与最低速的差。如果起点和终点不能到达，那么输出-1。

 */
public class MSTFindComfortablePath {

	static class Edge implements Comparable<Edge>{
		int u,v,w;
		public int compareTo(Edge e){
			return this.w - e.w;
		}
	}
	
//	static class Edge{
//		int u,v,w;
//	}
	
	static int[] pre;
	static Edge[] edges;
	static int max = Integer.MAX_VALUE;
	
	static int find (int k){//寻找k的根节点
		if(pre[k] == k)
			return k;
		return pre[k] = find(pre[k]);
	}
	
	static void merge(int x,int y){//合并集合
		int v1 = find(x);
		int v2 = find(y);
		if(v1 != v2)
			pre[v1] = v2;//左边集合变成右边子集合
	}
	
	static void init(int[] pre){//初始化
		for(int i = 1; i < pre.length; i++){
			pre[i] = i;
		}
	}
	
	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);
		int vertexNum = in.nextInt();
		int edgeNum = in.nextInt();
		pre = new int[vertexNum + 1];
		edges = new Edge[edgeNum];
		
		for(int i = 0 ; i < edgeNum; i++){
			edges[i] = new Edge();
			edges[i].u = in.nextInt();
			edges[i].v = in.nextInt();
			edges[i].w = in.nextInt();
		}
		
		//边权值从小到大排序：1.边结构需实现comparable接口 2.使用优先队列--最小堆
		Arrays.sort(edges);
		
//		PriorityQueue<Edge> graph = new PriorityQueue<>((v1,v2) ->v1.w - v2.w);
//		for(int i = 0 ; i < edgeNum; i++){
//			edges[i] = new Edge();//*!!!
//			edges[i].u = in.nextInt();
//			edges[i].v = in.nextInt();
//			edges[i].w = in.nextInt();
//			graph.add(edges[i]);
//		}

		
		
		int pathNum = in.nextInt();
		for(int i = 0; i < pathNum; i++){
			int start = in.nextInt();
			int end = in.nextInt();
			int ans = max;
			
			for(int j = 0; j < edgeNum; j++){
				//每个顶点初始化为独立的树：父结点是自身
				init(pre);
				
				for(int k = j ; k < edgeNum; k++){
					//按权值从小到大选择边，所选边的顶点若属于不同的树则合并为一棵树
					merge(edges[k].u, edges[k].v);
					
					if(find(start) == find(end)){//如果start和end连通，枚举“起点”和“满足条件之点”之差，选择乘坐过程中最高速度与最低速度的差最小的路径
						ans = Math.min(ans, edges[k].w - edges[j].w);
					}
				}
				
			}
			
			if(ans == max)//不存在
				ans = -1;
				
			System.out.println(ans);
		}
		in.close();
	}

}
/*

input: 
4 4
1 2 2
2 3 4
1 4 1
3 4 2
2
1 3
1 2

output:
1 //1-4-3 2-1=1
0 //1-2 2-2=0
 */

 

 

在实现方面的区别：

1、Kruskal算法在生成最小生成树的过程中产生的是森林，Prim算法在执行过程中始终都是一棵树；

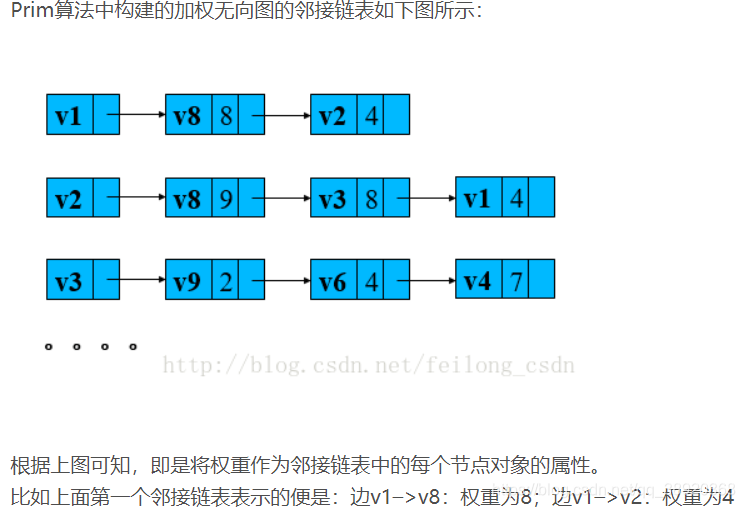
2、Kruskal不需要搜索每个顶点的邻接节点，而Prim中需要，所以Prim图构建时需要邻接链表表示加权无向图

 

MST----Prim 算法

1、图顶点对象及其属性定义：

public class VertexWG {
    String verName;  //名称
    int weight;  //权重
    double key;  //key是键顶点v与树中某一顶点相连的边中最小权值
    VertexWG parent;  //父对象
    VertexWG nextNode;  //下一个节点对象
}

2、最小堆：最小堆的顶点对象是Vertex，排序是通过Vertex的属性vertex.key进行排序的 
vertex.key是所有将v与树中某一顶点相连的边中最小权值，按约定如果不存在这样的边，则vertex.key=∞

 

• 对每个顶点对象进行初始化，并初始化优先级队列Q，使其包含所有初始化的节点； 
• 首先只要优先级队列不为空，root节点随机选取//从Q中选出v.key最小的顶点，然后遍历它的每一个邻接节点，当其邻接节点满足两个条件： 
• 1、该节点v仍在Q中 
• 2、该节点v满足w(u,v)< v.key 
• 满足上面条件边更新节点的key值信息和parent信息，直到while循环结束！
   

 数组实现：

private static void prim(int[][] graph,char[] vername, int verNum) {
		int[] lowcost = new int[verNum];//未遍历集合中顶点到已遍历集合中顶点的最小权值
		int[] pre = new int[verNum];//存取前驱结点--上一个加入到已遍历集合中去的顶点
		
		List<Character> list = new ArrayList<>();//存储加入结点的顺序
		
		int minweight, minindex, sum = 0;
		for(int i = 1; i < verNum; i++){
			lowcost[i] = graph[0][i];//每个点到顶点0的初始权值
			pre[i] = 0;
		}
		list.add(vername[0]);
		
		//初始加入第一个点，接下来加入剩下n-1个点
		for(int i = 1; i < verNum; i++){
			minweight = MAX;
			minindex = 0;
			
			// 遍历找距离集合最近的点
			for(int j = 1; j < verNum; j++){
				if(lowcost[j] != 0 && lowcost[j] < minweight){//顶点j没有遍历过，并且到已遍历集合的距离更小
					minweight = lowcost[j];
					minindex = j;
				}
			}
			
			if(minindex == 0) return;
			list.add(vername[minindex]);
			lowcost[minindex] = 0;//已遍历集合中的点lowcost为0
			
			sum += minweight;
			
			System.out.println(vername[pre[minindex]] + "->" + vername[minindex] + ":"+minweight );
			
			//加入新顶点后，更新未遍历集合中其它点到集合的距离
			for(int k = 1; k < verNum; k++){
				if(lowcost[k] != 0 && lowcost[k] > graph[minindex][k]){
					lowcost[k] = graph[minindex][k];
					pre[k] = minindex;
				}
			}
		}
		
		System.out.println("最小生成树权值:" + sum);
	}

 

DFS

可以回溯，内存开销小（不需要存孩子结点）

应用：

• 拓扑排序
• 查找连通分量
• 查找图的关节点（割点--移除该顶点之后得到两个连通分量）
• 查找强连通分量
• 解决类似迷宫的问题

public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        //mark
		Set<Integer> visited = new HashSet<>();
		visited.add(0);
		
		//DFS-Stack
		Stack<Integer> stack = new Stack<>();
		stack.add(0);
		
		while(!stack.isEmpty()){
			List<Integer> keys = rooms.get(stack.pop());
			
			for(int key:keys){
				if(!visited.contains(key)){
					visited.add(key);
					stack.add(key);
				}
			}
		}
		
		return visited.size() == rooms.size();
    }

例题1： 

public int numIslands(char[][] grid) {
	       int res = 0;
	        if(grid == null || grid.length == 0)
	        	return 0;
	        
	        for(int i = 0; i < grid.length; i++){
	        	for(int j = 0; j < grid[0].length; j++){
	        		if(grid[i][j] == '1'){
	        			dfs(grid,i,j);
	        			res++;
	        		}
	        	}
	        }     
			return res;
	    }
	/**
	     * Marks the given site as visited, then checks adjacent sites.
	     * 
	     * Or, Marks the given site as water, if land, then checks adjacent sites.
	     * 
	     * Or, Given one coordinate (i,j) of an island, obliterates the island
	     * from the given grid, so that it is not counted again.
	     * 
	     *absorbing all surrounding connected lands into one!!!
	     */
		private void dfs(char[][] grid, int i, int j) {
	        //check whether it is a land
			if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0')
				return;
			
			//avoid revisit
			grid[i][j] = '0';
			
	        //checks adjacent sites
			dfs(grid,i+1,j);
			dfs(grid,i-1,j);
			dfs(grid,i,j+1);
			dfs(grid,i,j-1);	
		}

例题2：

/*
	 * Battleships can only be placed horizontally or vertically. In other words, they can only be made of the shape 1xN (1 row, N columns) or Nx1 (N rows, 1 column), where N can be of any size.
At least one horizontal or vertical cell separates between two battleships - there are no adjacent battleships.
	 */
	public int countBattleships1(char[][] board) {
		  int num = 0;
	       for(int i = 0; i < board.length; i++){
	    	   for(int j = 0; j < board[0].length;j++){
	    		   if(board[i][j] == '.'){
	    			  continue;
	    		   }
	    		   
	    		   //avoid counting the same ship
	    		   if(i > 0 && board[i - 1][j] == 'X'){
	    			   continue;
	    		   }
	    		   if(j > 0 && board[i][j - 1] == 'X'){
	    			   continue;
	    		   }
	    		  
	    		num++;
	    		  
	    	   }
	       }
	       return num;
	    }
	
	public int countBattleships2(char[][] board) {
		  int num = 0;
	       for(int i = 0; i < board.length; i++){
	    	   for(int j = 0; j < board[0].length;j++){
	               //if it is a ship,sink 'x' around it
	               //absorbing all surrounding connected lands into one!!!
	    		   if(board[i][j] == 'X'){
	    			   num++;
	    			   sink(board,i,j);
	    		   }
	    	   }
	       }
	       return num;
	    }

	private void sink(char[][] board, int i, int j) {
		if(i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] == '.'){
			return;
		}
			
		//sink the battle,avoid revisit
		board[i][j] = '.';
	        
	    // sink 'x' around it
		sink(board, i + 1, j);
		sink(board, i - 1, j);
		sink(board, i, j + 1);
		sink(board, i, j - 1);
	}

 

 

拓扑排序： 

 

 

BFS 

不能回溯

应用：

• 查找图中连通分量
• 查找某个连通图中的所有结点
• 查找两结点间的最短路径
• 测试图的二分性

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class BFSTreeLevelOrder102 {

	
	 public class TreeNode {
	     int val;
	     TreeNode left;
	     TreeNode right;
	     TreeNode(int x) { val = x; }
	 }

	 public List<List<Integer>> levelOrder(TreeNode root) {
		 List<List<Integer>> result = new ArrayList<>();
		 
		 if(root == null)
			 return result;
		 
		 //BFS--queue-->add children
		 Queue<TreeNode> queue = new LinkedList<>();
		 queue.add(root);
		 
		 while(!queue.isEmpty()){
			 int size = queue.size();
			 List<Integer> levelVal = new ArrayList<>();
			 
			 for(int i = 0; i < size; i++){			 
				 TreeNode temp = queue.remove();
				 
				 levelVal.add(temp.val);
				 
				 if(temp.left != null){
					 queue.add(temp.left);
				 }
				 if(temp.right != null){
					 queue.add(temp.right);
				 }
			 }
			 result.add(levelVal);
		 }
		 return result;
	 }

}

 

 

最短路径----Dijkstra,有权图

最短路径----Bellman-Ford,含有负边的有权图 

最短路径----Floyd