【蓝桥杯】 基础练习 矩形面积交

问题描述
　　平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。
输入格式
　　输入仅包含两行，每行描述一个矩形。
　　在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过10^7的实数表示。
输出格式
　　输出仅包含一个实数，为交的面积，保留到小数后两位。
样例输入
1 1 3 3
2 2 4 4
样例输出
1.00

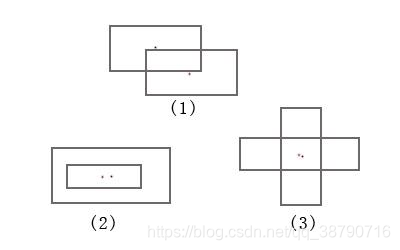
个人思路：这道题更像是一道找规律题吧，可以将两个矩形相交的情况都画出来，只有几种情况(如上图的几种)，然后再认真观察，很容易发现相交得到的那个矩形的面积其实就等于夹在中间的两个$x$之差 $\ast$ 两个$y$之差,那么问题就转换成了找夹在中间的$x$与$y$

相交得到的矩形的左边的$x(m2)$其实就是$max(min(x1,x2),min(x3,x4))$，右边的$x(m1)$则为$min(max(x1,x2),max(x3,x4))$，那么同理y也是如此 【$x1、x2、x3、x4$为题目要求输入的两对相对顶点的$x$值】，即得到相交矩形的面积为$(m1-m2)\ast (n1-n2)$ 【$n1、n2$为得到的y值】

如果相交，那按照这种方式得到的$m1、m2、n1、n2$必然满足$m1>m2$ && $n1>n2$，所以如果不满足则不相交

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
int main()
{
	double x1,y1,x2,y2;
	double x3,y3,x4,y4;
	double m1,m2,n1,n2;
	cin>>x1>>y1>>x2>>y2>>x3>>y3>>x4>>y4;
	m1=min(max(x1,x2),max(x3,x4));
	n1=min(max(y1,y2),max(y3,y4));
	m2=max(min(x1,x2),min(x3,x4));
	n2=max(min(y1,y2),min(y3,y4));
	if(m1>m2&&n1>n2){
		cout<<setiosflags(ios::fixed)<<setprecision(2);
		cout<<(m1-m2)*(n1-n2)<<endl;
	}
	else
		cout<<"0.00"<<endl;
	return 0;
}