最近点对算法

最新推荐文章于 2021-04-25 18:32:39 发布

隆1

最新推荐文章于 2021-04-25 18:32:39 发布

阅读量1.1k

点赞数

CC 4.0 BY-SA版权

分类专栏：计算几何文章标签：算法计算几何最近点对

本文链接：https://blog.youkuaiyun.com/qq_38786088/article/details/89487934

该博客介绍了如何在二维平面上寻找n个点的最近点对。首先，问题描述了要找到所有点对中距离最短的一对。接着，博客详细探讨了两种方法：一是蛮力法，通过两遍循环比较所有点对，时间复杂度为O(n^2)；二是分治法，通过对点按x坐标排序并进行递归处理，最终达到O(nlogn)的时间复杂度。博客还通过实例解释了分治法的工作原理，并提到了相关编程题目。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最近点对算法

问题描述

二维平面上n个点，求最近的两点距离？

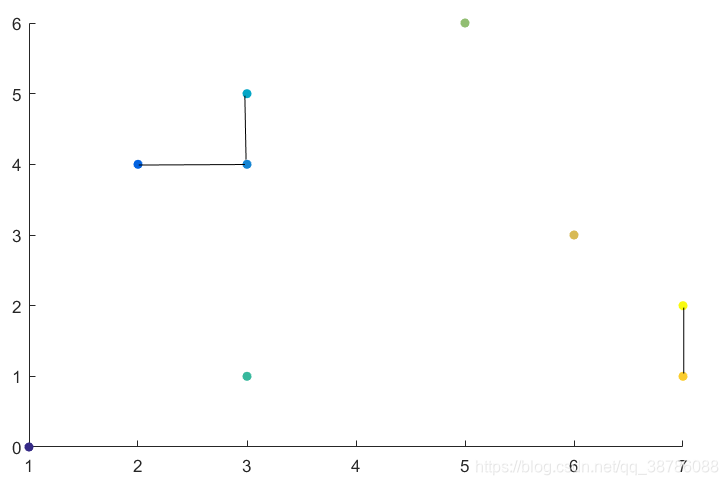
如例：
    P1 (1，0)、P2 (2，4)、P3 (3，4)
    P4 (3，5)、P5 (3，1)、P6 (5，6)
    P7 (6，3)、P8 (7，1)、P9 (7，2）
最短距离点对有3对，(P2,P3)、(P3,P4)、(P8,P9),最短距离为1.

方法一：蛮力法

两遍循环，枚举任意两点P[i] 、P[j] (i ≠ j) ，求出距离，一一比较，得到最短距离mind.

时间复杂度：两重循环， $O(n^2)$ .

暴力法：ClosePoint(P[],n)
/*
*输入： 点{x,y}数组P及个数n
*输出： 输出最近的两点距离
*/
if n < 2 then   //无点对
	return INF 
endif

if n = 2 then  //返回仅有两点距离
	return dist{
     
     P[0],P[1]}
endif

mind <-- INF  // 标记：最短距离
for i = 1 to n-1 do
	for j = i + 1 to n do
		mind <-- min