时间差分算法

时间差分算法

Sarsa算法

Derive TD Target

• 回顾Discounted Return，不难推出这个时刻的回报等于这个时刻的奖励加上下个时刻的回报乘以$\gamma$

• 我们使用$U_t=R_t+\gamma \cdot U_{t+1}$来推导TD target，通常认为奖励$R_t$依赖于t时刻的动作$A_t$和状态$S_t$，以及t+1时刻的状态$S_{t+1}$，根据定义状态价值函数$Q_{\pi }(s_t,a_t)$是回报$U_t$的条件期望，这里我们假设已经观测到了当前的状态$s_t$和动作$a_t$，期望是对未来的所有的动作和状态求的，消除掉未来的不确定性。这个时候我们可以将期望中的$U_t$使用上面得到的等式替换掉。这样我们就可以将期望分解为$R_t$的期望和$U_{t+1}$的期望。研究$U_{t+1}$的期望的研究，因为$Q_{\pi }(S_{t+1},A_{t+1})=U_{t+1}$，所以可以替换。
  

• 通过上面的推导我们可以得到$Q_{\pi }(s_t.a_t)=\mathbb{E}[R_t+\gamma \cdot Q_{\pi }(S_{t+1},A_{t+1})]$，因为左右两边都有$\pi$函数，所以这个等式对任何的策略$\pi$都成立，等式右边有期望，因为求期望很困难，通常我们对期望做蒙特卡洛近似。可以将等式右边的$R_t$近似为观测到的奖励$r_t$，$S_{t+1},A_{t+1}$都是随机变量，我们可以用观测到的值$s_{t+1},a_{t+1}$，这样我们就可以得到近似值$Q_{\pi }(s_{t+1},a_{t+1})$，这样我们就得到了期望的蒙特卡洛近似，将这个近似值叫做TD target $y_t$。
  

• 通过上一步推导我们将t+1时刻的期望近似成了TD target $y_t$，$y_t$部分基于真实观测到的奖励，部分基于预测。TD Learning的想法就是鼓励动作价值函数$Q_{\pi }(s_t,a_t)$接近$y_t$，这是因为动作价值函数$Q_{\pi }(s_t,a_t)$全是估计，而$y_t$部分基于真实值，所以我们认为$y_t$更可靠。

Sarsa: Tabular Version

• 我们想要学习动作价值函数$Q_{\pi }(s,a)$，它的输入状态s和动作a，如果输入的状态和动作是有限的，那么我们可以画一个表格，表格中的一列对应一个动作，一行对应一个状态，表格的一个元素对应一个动作价值。我们要做的就是使用Sarsa算法来更新表格，每次更新一个元素。

• 每次观测到一个四元组，$(s_t,a_t,r_t,s_{t+1})$，一个四元组称为一个transition。将动作记为：$a_{t+1}$。然后计算TD target $y_t$，一部分是真实的奖励$r_t$，另一部分是动作价值函数给下一个动作打的分数。动作价值函数可以通过查阅表格得到$s_{t+1}$行，$a_{t+1}$列的元素， 通过查表还可以知道$Q_{\pi }(s_t,a_t)$的值，这样就可以得到TD error了，这样就可以使用可以使用TD error来更新，将更新的值写入表格相应的位置。

Sarsa’s Name

• Sarsa名字的由来

Sarsa: Neural Network Version

• 如果状态空间很大，使用表格法就会很难学习。可以用神经网络来近似动作价值函数，得到的神经网络就叫做价值网络。
• 使用神经网络来近似动作价值函数，记为：$q(s,a;w)$，参数记为：w。这里的动作价值函数和价值网络都和策略$\pi$有关。价值网络的输入是当前的状态，输出是所有动作的价值的向量。

• 之前我们在Actor-Critic方法中使用到了价值网络q，它被称为Critic，用来评价Actor的表现。价值网络的参数w，一开始是随机初始化的，我们要用观测到的奖励来更新w。TD target $y_t$一部分是真实的奖励$r_t$，另一部分是价值网络q对t+1时刻价值的估计，这样我们可以计算TD error，我们希望TD error的值越小越好。我们将损失函数记为：${\delta }^2/2$. 对损失函数关于参数求梯度，最后使用梯度下降更新w。

Summary

Q-Learning

Sarsa VS Q-Learning

• Sarsa和Q-Learning都是TD算法，但是他们解决的问题不同。Sarsa用来训练动作价值函数$Q_{\pi }(s,a)$
• TD target为当前时刻的奖励$r_t$以及$\gamma \cdot Q_{\pi }(s_{t+1},a_{t+1})$的和
• 我们之前使用Sarsa来更新价值网络

• Q-learning用来训练最优动作价值函数$Q^{\ast }(s,a)$
• Q-learning的TD target: $y_t=r_t+\gamma \cdot \underset{a}{\max }{Q}^{\ast }(s_{t+1},a)$
• 我们使用Q-learning来更新DQN

Derive TD Target

• 首先推导Q-learning的TD target
• 在之前我们证明了$Q_{\pi }=\mathbb{E}[R_t+\gamma \cdot Q_{\pi }(S_{t+1},A_{t+1})]$，对于任何的策略$\pi$该等式都成立
• 我们将最优的策略记为：${\pi }^{\ast }$，上面的等式对最优的策略${\pi }^{\ast }$也成立，所以我们就可以得到$Q_{{\pi }^{\ast }}=\mathbb{E}[R_t+\gamma \cdot Q_{{\pi }^{\ast }}(S_{t+1},A_{t+1})]$，我们通常将$Q_{{\pi }^{\ast }}$记为：$Q^{\ast }$，他们都表示最优动作价值函数。所以我们可以写为期望的形式$Q^{\ast }(s_t,a_t)=\mathbb{E}[R_t+\gamma \cdot Q^{\ast }(S_{t+1},A_{t+1})]$

• $Q^{\ast }(s_t,a_t)=\mathbb{E}[R_t+\gamma \cdot Q^{\ast }(S_{t+1},A_{t+1})]$，$Q^{\ast }$可以评价动作的好坏，给定状态$S_{t+1}$，$Q^{\ast }$可以给所有的动作打分，然后Agent会执行分数最高的动作，给定状态$S_{t+1}$选出的动作，一定是使$Q^{\ast }$最大化的动作。所以$A_{t+1}=\underset{a}{\mathrm{argmax}}{Q}^{\ast }(S_{t+1},a)$，所以$Q^{\ast }(S_{+}t+1,A_{t+1})$可以写为对$Q^{\ast }(S_{t+1},a)$关于动作a求最大化，因为$A_{t+1}$是最优动作，所以可以最大化$Q^{\ast }$

• 由上面我们可以推导出下面的公式，可以得到下面的等式

• 由于我们求期望很复杂，所以我们可以对期望求蒙特卡洛近似，我们可以将奖励$R_t$近似成为观测到的奖励$r_t$，期望中有状态$S_{t+1}$我们使用观测到的状态$s_{t+1}$代替，这样我们就可以得到近似值$\underset{a}{\max }{Q}^{\ast }(s_{t+1},a)$，这样我们就得到了期望的蒙特卡洛近似$r_t+\gamma \cdot \underset{a}{\max }{Q}^{\ast }(s_{t+1},a)$，将这个近似值记作TD target $y_t$，因为$y_t$是基于真实值的，所以它比等式左边更加接近真实值。
  

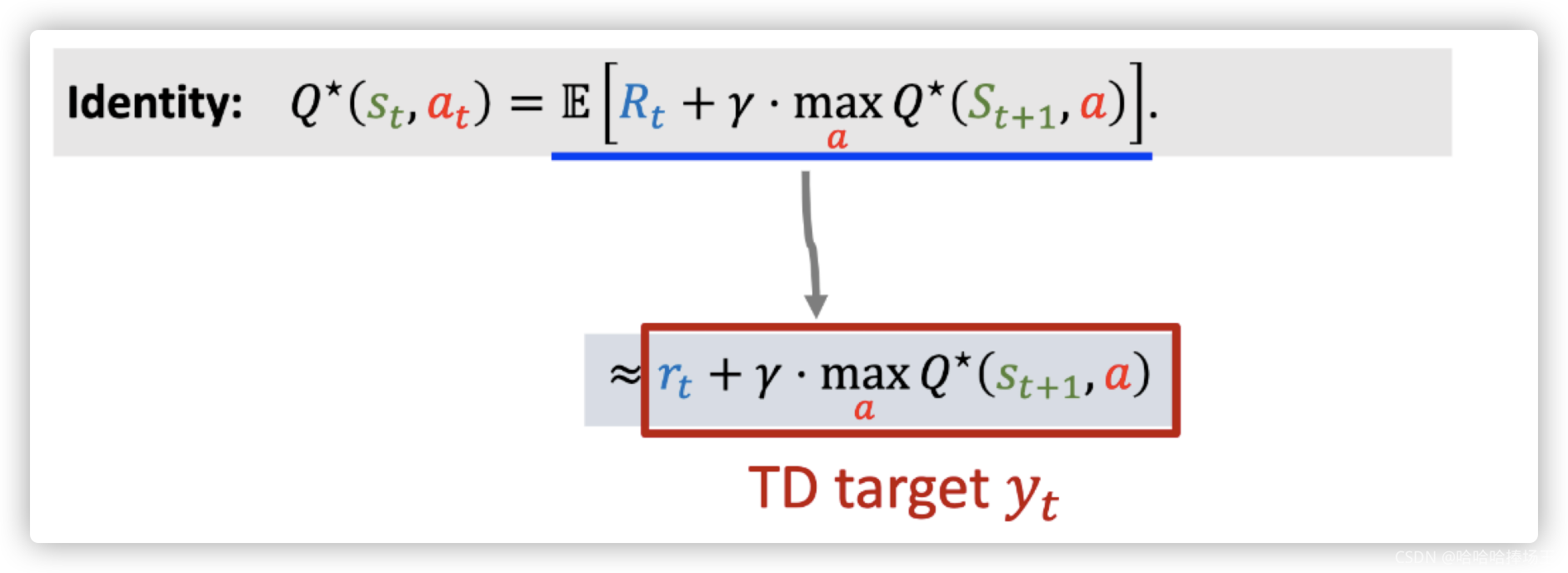
Q-Learning: Tabular Version

• 每次观测到一个transition: $(s_t,a_t,r_t,s_{t+1})$
• 用$s_{t+1}$来计算TD target $y_t$，这里要对$Q^{\ast }$关于a求最大化，$Q^{\ast }$就是表格，我们要查表，找到状态$s_{t+1}$对应的行，找出这一行最大的元素，最大的元素就是最大值

• 然后计算TD error，最后使用TD error来更新$Q^{\ast }$

Q-Learning: DQN Version

• DQN是对最优动作价值函数$Q^{\ast }$的近似，

• DQN控制Ageng，通过最大化Q函数，得到动作，让Agent执行

• 我们使用收集到的transition来更新w，让DQN得到的价值更加准确
  

• 训练DQN最常用的算法就是Q-Learning，它是一种TD算法，以前说过，这里回顾一下。

  • 每次观测到一个transition
  • 然后计算TD target，既要用到真实值，也要用到预测
  • 计算TD error，我们的算法希望得到的TD error尽量小
  • 所以做一次梯度下降来更新网络的参数，这样就可以见效TD error了

Summary

Multi-Step TD Target

Sarsa vs Q-Learning

• 上面我们可以看到不管我们使用什么方法，它都包含一个奖励$r_t$

Using One Reward

• 使用两个奖励来更新，效果更好

Multi-Step Return

• 之前我们得到：$U_t=R_t+\gamma \cdot U_{t+1}$，我们可以使用$R_{t+1}+\gamma \cdot U_{t+2}$来替换$U_{t+1}$，这样我们就可以得到$U_t=R_t+\gamma \cdot R_{t+1}+{\gamma }^2\cdot U_{t+2}$，这样我们可以让回报包含两个奖励，同样的道理我们可以让回报包含多个奖励，将下面最后得到的公式叫做Multi-Step Return

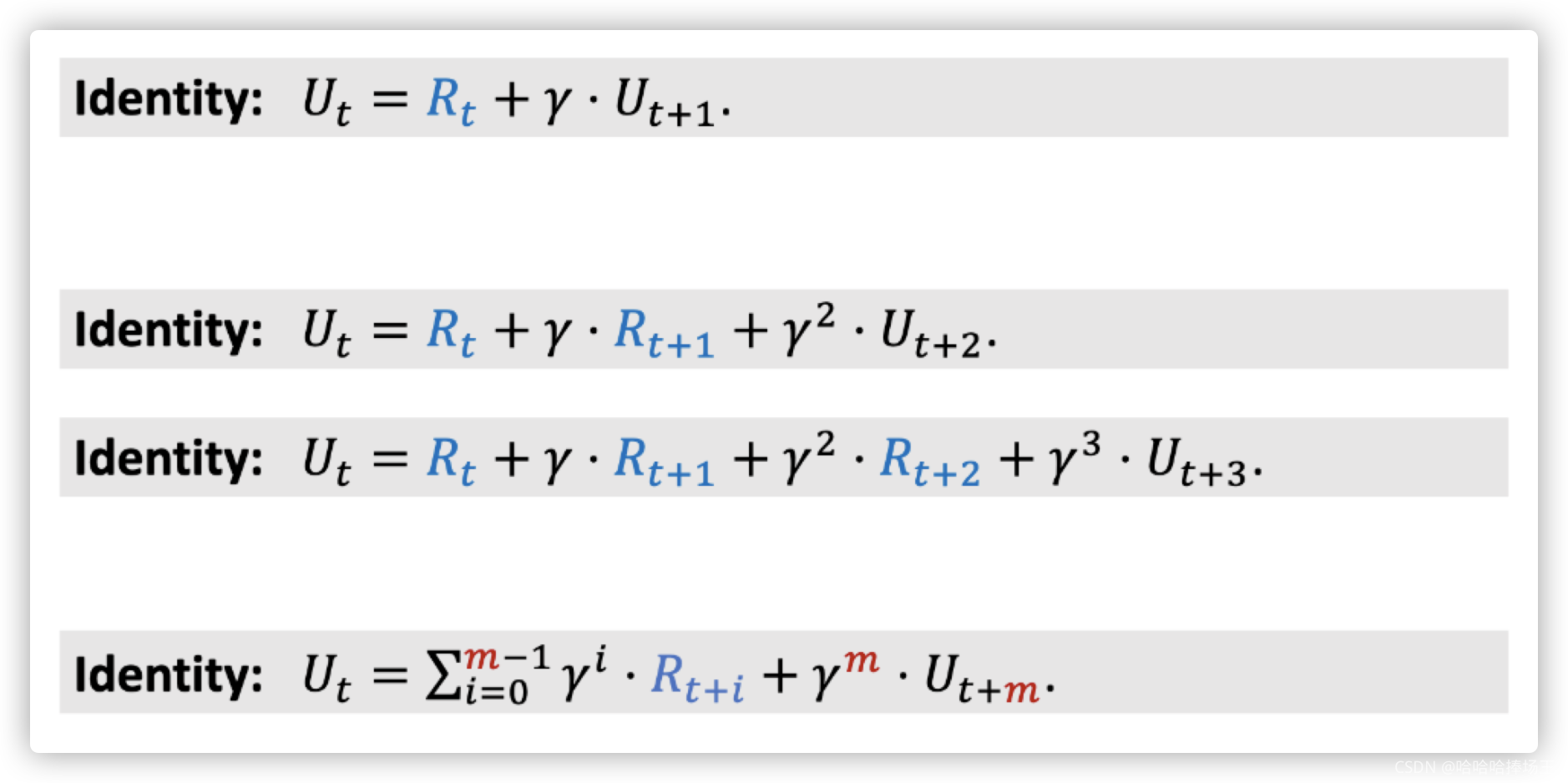
• 由上面我们得到的回报的公式，我们可以推导出TD target $y_t$的公式，下面就是得到的公式，其中小r表示真实的奖励，后面一项是期望。
  
  

One-Step vs Multi-Step