Weakly-Supervised Discovery of Geometry-Aware Representation for 3D Human Pose Estimation CVPR 2019

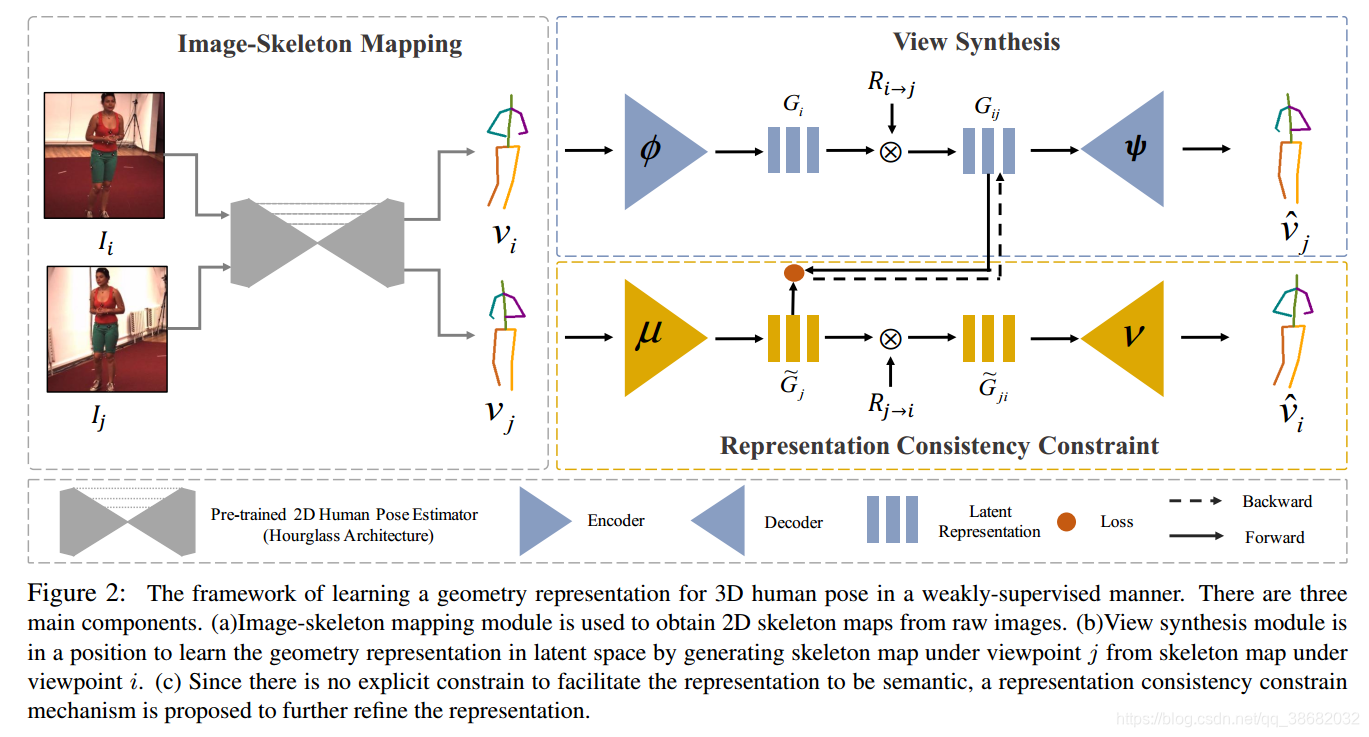
gold:

learn a geometry-aware 3D representation $\mathcal{G}$ for the human pose

discover the geometry relation between paired images $(I_t^i,I_t^j)$
which are acquired from synchronized and calibrated cameras

• $i,j$：different view point
• $t$:acquiring time acquiring

main components

• image skeleton mapping
• skeleton-based view synthesis
• representation consistency constraint

image-skeleton mapping

input raw image pair $(I_t^i,I_t^j)$ with size of $W\times H$

• $i,j$:different view point ,(synchronized and calibrated cameras $i,j$)

$C_t^i,C_t^j$:$K$ keypoint heatmaps from a pre-trained 2D human pose eastimator

We follow previous works [45, 20, 18] to train the 2D estimator on MPII dataset.

constructed 8 pixels width 2D skeleton maps from heatmaps

binary skeleton maps pair $(S_t^i,S_t^j)$,St(⋅)∈{0,1}(K−1)×W×HS_t^{(\cdot)}\in\{0,1\}^{(K-1)\times W \times H}St(⋅)​∈{0,1}(K−1)×W×H

Geometry representation via view synthesis

training set T={(Sti,Stj,Ri→j)}\mathcal T = \{(S^i_t,S^j_t,R_{i\to j})\}T={(Sti​,Stj​,Ri→j​)}

• pairs of two views of projection of same 3D skeleton $(S_t^i,S_t^j)$
• relative rotation matrix $R_{i\to j}$ from coordinate system of camera $i$ to $j$

Straightforward way for learning representation in unsupervised/weakly-supervised manner is to utilize auto-encoding mechanism reconstrcting input image.

• no geometry structure information
• nor provides more useful information for 3D pose estimation than 2D coordinates

novel ‘skeleton-based view synthesis’ generate image under a new viewpoint.
Given an image under the known viewpoint as input

source domain : (input image） Si={Sti}i=1V\mathcal S^i = \{S^i_t\}^V_{i=1}Si={Sti​}i=1V​

• $V$ :amount of viewpoints

target domain :generate image Sj={Stj}i=1V\mathcal S^j = \{S^j_t\}^V_{i=1}Sj={Stj​}i=1V​

• $j̸=i$

encoder $\varphi :{\mathcal{S}}^i\to \mathcal{G}$

• source skeleton $S_t^i\to {\mathcal{S}}^i$ into a latent space $G_i\in \mathcal{G}$

decoder $\psi :{\mathcal{R}}_{i\to j}\times \mathcal{G}\to {\mathcal{S}}_i$

• ratation matrix $R_{i\to j}$
• $G_i$ as the set of $m$ discrete points on 3$\eta$-dimensional space
  in practice: $G=[g_1,g_2,...g_M{]}^T,g_m=(x_m,y_m,z_m)$

$$L_{\ell 2}(\varphi \cdot \psi ,\theta )=\frac{1}{N^T}\sum \Vert \psi (R_{i\to j}\times \varphi (S_t^i))-S_t^j\Vert$$

Representation consistency constraint

image skeleton mapping + view synthesis （previous two steps）lead to unrealistic generation on target pose when there are large self occlusions in source view

Since there is no explicit constraint on latent space to facilitate $\mathcal{G}$ to be semantic

We assume there exists an inverse mapping (one-to-one) between source domain and target domain, on the condition of the known relative rotation matrix. We could find:

a encoder $\mu :{\mathcal{S}}^j\to \mathcal{G}$

• maps target skeleton $S_t^j$ to latent space ${\tilde{G}}_j\in \mathcal{G}$

a decoder $\nu :R_{j\to i}\times G\to S_t^i$

• maps representation ${\tilde{G}}_j$ back to source skeleton $S_t^i$
• ${\tilde{G}}_i$ and $G_i$ should be the same shared representation on $\mathcal{G}$ with different rotation-related coefficients ------namely representation consistency

$$l_{rc}=\sum _{m=1}^M\Vert f\times G_i-{\tilde{G}}_i{\Vert }^2$$

• $f=R_{i\to j}$ rotation-related transformation that map $G_i$ to ${\tilde{G}}_j$
• a bidirectional encoderdecoder framework
  • $generator(\varphi ,\psi )$,$G_{ij}$:rotated $G_i$
  • $generator(\mu ,\nu )$
    

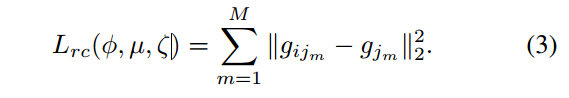
total loss of the bidirectional model

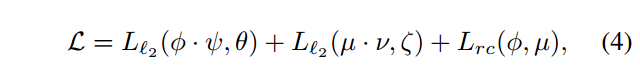
where θ and ζ denotes the parameters of two encode-decoder networks, respectively.

3D human pose estimation by learnt representation

given: monocular image $I$
goal : b={(xp,yp,zp)}p=1P\bold b = \{(x^p,y^p,z^p)\}^P_{p=1}b={(xp,yp,zp)}p=1P​,P body joints,$\mathbf{b}\in \mathcal{B}$

function $\mathcal{F}:\mathcal{I}\to \mathcal{B}$ to learn the pose regression

2 fully connect layer