力扣11盛最多水的容器

力扣11盛最多水的容器

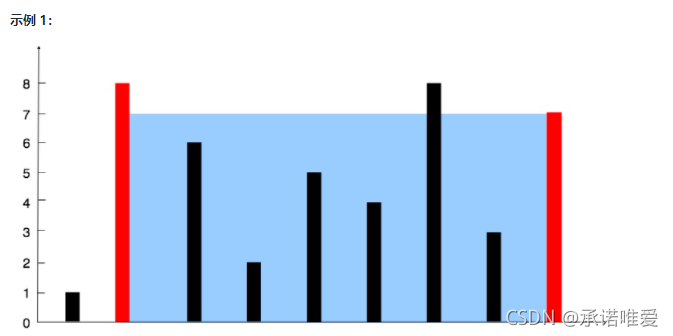
题目描述：给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

示例1输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例2输入：height = [4,3,2,1,4]
输出：16

解题思路：查找最大面积，首先最容易想到的就是由下标0开始至下标max-1反向遍历查找最大面积：

class Solution {
    public int maxArea(int[] height) {
        int max = 0;
        for (int i = 0; i < height.length; i++) {
            int volumn = dealLogic(i,height.length-1,height);
            max = volumn > max ? volumn : max;
        }
        return max;
    }

    public int dealLogic(int left, int right, int[] array) {
        int max = 0;
        while (left < right) {
            int volumn = 0;
            int x = right - left;
            if (array[left] <= array[right]) {
                volumn = x * array[left];
            }
            if (array[left] > array[right]) {
                volumn = x * array[right];
            }
            max = volumn > max ? volumn : max;
            right--;
        }
        return max;
    }
}

但很不幸，这样写一提交，超时了？？？这里用了两层循环都超时，说明需要寻找O（n）的路子。
仔细观察题目可以发现，当array[left] < array[right]的时候，没必要总是right–，此时应left++，逐渐往高的点查，往中心靠拢。因此可以修改为：

class Solution {
    public int maxArea(int[] height) {
       int left = 0,right = height.length-1;
            int max = 0;
            while (left < right) {
                int volumn = 0;
                int x = right - left;
                if (height[left] <= height[right]) {
                    volumn = x * height[left];
                }
                if (height[left] > height[right]) {
                    volumn = x * height[right];
                }
                max = volumn > max ? volumn : max;
                if (height[left] < height[right])
                    left++;
                else
                    right--;
            }
            return max;
    }
}

运行结果截图：