机器学习系列_逻辑回归

1、关于逻辑回归

1.1 线性回归（Linear Regression ）

首先我们需要了解线性回归（Linear Regression ）,线性回归主要是用来刻画自变量和因变量之间的关系（所以通常可以用线性回归模型做预测）。在一元线性回归中，只含有一个自变量x，在二维平面中拟合成直线f(x) = kx + b，如下图所示：

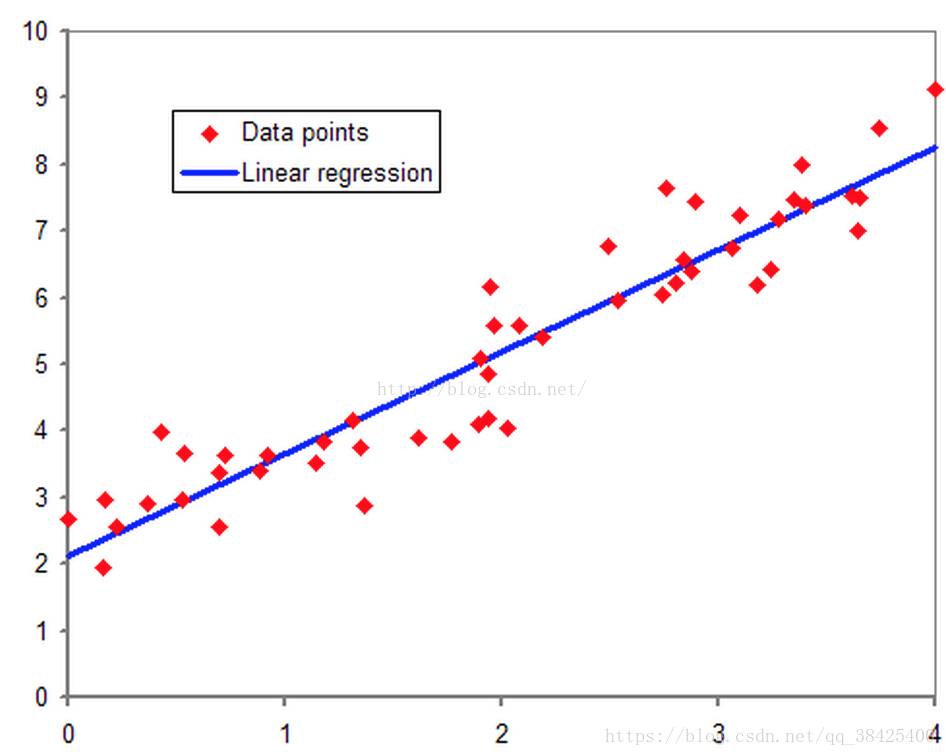
当自变量不少于两个时，属于多元线性回归，形如函数y = b0 + b1x1 + b2x2 + e，回归系数代表相对应自变量的重要程度。

1.2 逻辑回归（Logistic Regression）

逻辑回归与线性回归模型针对的应用不同，当我们对连续值进行预测时，比如对于房价，分数等。如果我们已经训练好一个模型f(x)，将测试集代入模型中即可得到我们想要的结果。然而不同的是，逻辑回归模型最常用于二分类问题当中，比如我们要预测西瓜是否成熟，通过分析年龄、性别、体质指数、平均血压、疾病指数等指标，判断一个人是否换糖尿病等。我们所需要的预测结果只是0（否），1（是）。因此有一个神奇的Sigmoid函数（如下）：

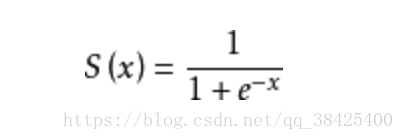
Sigmoid 函数图像如下：

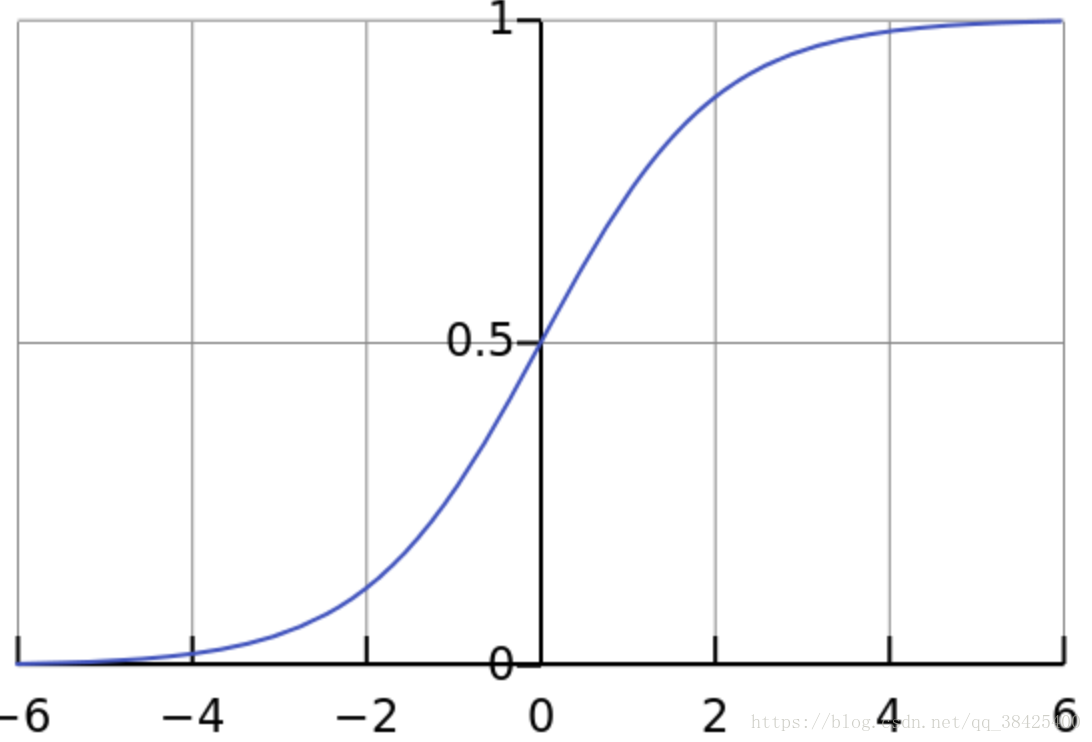
在上图中，我们可以看出Sigmoid函数值域在（0，1），所以如果当我们将线性回归模型中的预测值代入Sigmoid函数自变量x中，则可以将所有预测的连续值规约到（0，1），且我们规定Sigmoid函数值大于0.5时取1（代表是），小于0.5时取0（代表否）。

2、回归模型中的参数的求法

2.1 线性回归模型的损失函数（均方误差MSE）

$$cost=\frac{1}{m}\sum _{i=1}^m(y-f(x){)}^2$$
其中 f(x)代表真实值，f1(x)代表预测值。
线性回归模型试图学习如下公式：
$$f(x_i)={\omega }^T\ast X_i$$
将公式代入损失函数中，所以损失函数如下：
$$cost=\frac{1}{m}\sum _{i=1}^m(y-{{\omega }^T\ast X_i)}^2$$
所以在线性回归中我们需要找到令损失函数cost最小的特征系数omega的最优解。
最后结果等于如下：
$$\theta =(X^T\ast X{)}^{-1}{X}^{T}y$$

2.2 逻辑回归模型的损失函数

首先逻辑回归基本框架如下：

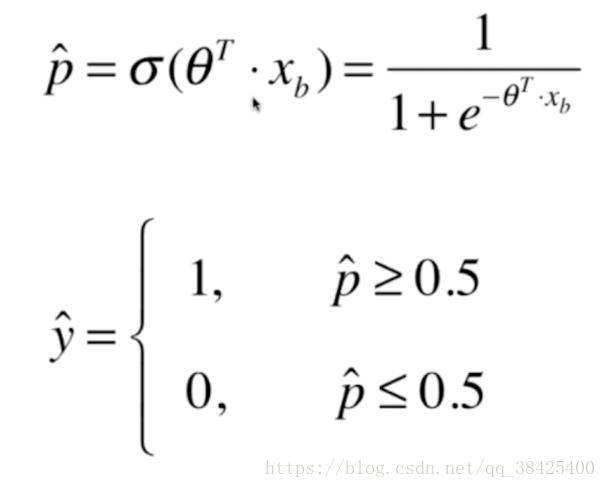
每拿一组样本xb，得到一个概率值，如果概率值大于等于0.5，则分类为1，概率值小于等于0.5，则分类为0。
逻辑回归损失函数的定义并不像线性回归那么简单，参考资料可以如下定义损失函数：


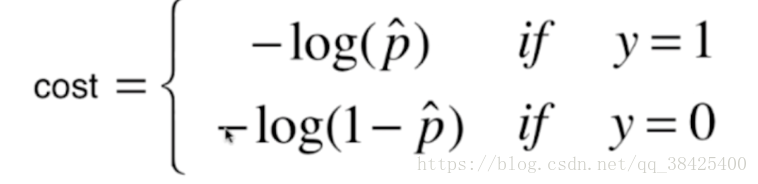
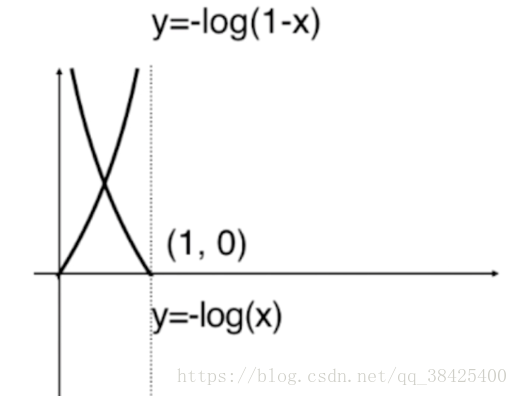
其中y代表样本真值，如果真实值为1，则当预测值p越小时，cost越大，如果真实值为0，则当预测值p越大时，cost越大。
损失函数可以写成如下形式：

​
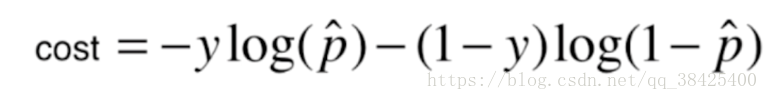
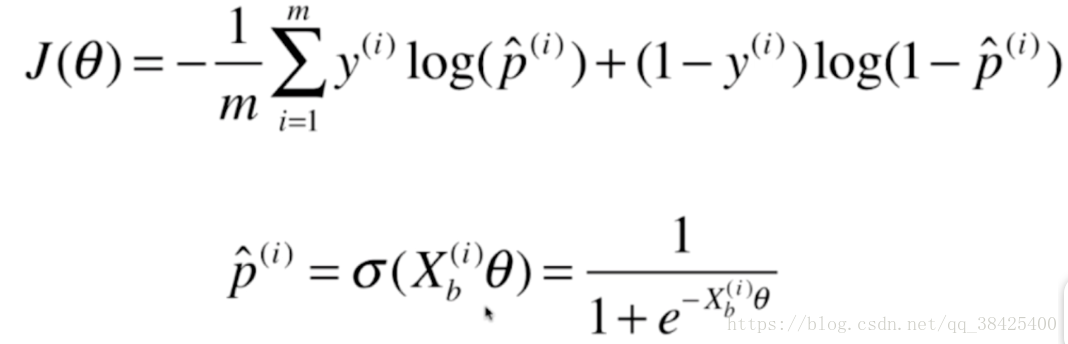
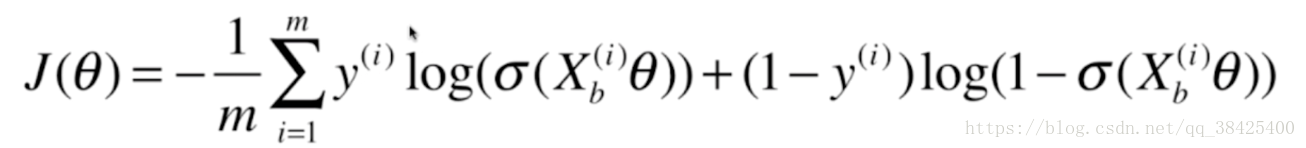其中y代表真实值，Xb代表给的样本特征，我们需要做的是利用梯度下降法找到一组theta，使就j(theta)最小。