线性代数-行列式

行列式定义

• det(A) ：行列式A
• 行列式是个数，n行n列 $n\ast n$个数组成，一定为方阵
• 二阶行列式 求值：主对角线相乘 -副对角线相乘
• $A_{ij}=(-1{)}^{i+j}{M}_{ij}$ 。$A_{ij}$是代数余子式，有符号；$M_{ij}$为余子式，没有符号

行列式性质

• 转置值不变
• 可按任意行列展开
  
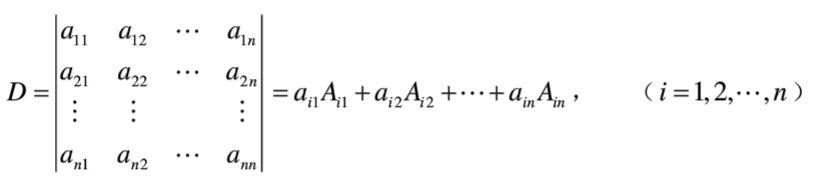
  • 某一行每个元素乘以每个元素对应的代数余子式求和，即为行列式的值。
    
  • 若乘以非对应的代数余子式，则结果为0
• 某行有共因子可按行提取
• 交换两行，值变号。（两行相等值为0）
• 两行元素成比例，值为0
• 把某行元素乘一个数，加到另一行上，值不变
• 行列式拆行相加性
  

行列式计算

• 一般利用行列式性质，将行列式化为三角行列式进行计算。
  • 第一行只保留第一个元素，第二行只保留前两个元素，以此类推
• 将某行化为只有极少非零元素，按该行展开

Laplace 展开定理

若在n阶行列式D中选定k个行，($1\le k<n$)，则行列式D的值等于这k个行所产生的所有k阶子式与他们对于的代数余子式对于的乘积之和。

Gramer法则

• 系数矩阵对应的行列式不等于0(系数矩阵满秩)，有唯一解。
  

齐次线性方程组有非零解时，行列式等于0

reference

东北大学 线性代数mooc https://www.icourse163.org/course/NEU-1001638002