代码随想录算法训练day58---图论系列3《岛屿问题3》

已于 2025-02-20 03:21:54 修改
阅读量770 收藏 15
点赞数 13
文章标签： 算法 c++
于 2025-02-14 16:41:59 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_38365428/article/details/145618806
版权

代码随想录算法训练

—day58

文章目录

前言

今天是算法营的第57天，希望自己能够坚持下来！
今天继续图论part！今日任务：
● 101.孤岛的总面积
● 102.沉没孤岛
● 103.水流问题
● 104.建造最大岛屿

一、101.孤岛的总面积

卡码网题目链接
文章讲解

思路：
本题要求找到不靠边的陆地面积，那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋，然后再去重新遍历地图 统计此时还剩下的陆地就可以了。

遍历地图周围四个边，将靠地图四边的陆地（绿色）都标记成水
在这里插入图片描述
然后再遍历地图，找到剩余的岛屿：
在这里插入图片描述

深搜

代码如下：

#include<iostream>
#include<vector>
using namespace std;
 
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
 
void dfs(vector<vector<int>>& grids, int x, int y) {
    if (grids[x][y] == 0) return;
    grids[x][y] = 0;
    count++;
     
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
         
        if (nextx < 0 || nextx >= grids.size() || nexty < 0 || nexty >= grids[0].size()) continue;
        dfs(grids, nextx, nexty);
    }
}
 
int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grids(n, vector<int>(m, 0));
     
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grids[i][j];
        }
    }
     
    //将接触边缘的岛屿先标记成水
    //从左侧和右侧向中间遍历
    for (int i = 0; i < n; i++) {
        if (grids[i][0] == 1) dfs(grids, i, 0);
        if (grids[i][m-1] == 1) dfs(grids, i, m-1);
    }
    //从上面和下面向中间遍历
    for (int j = 0; j < m; j++) {
        if (grids[0][j] == 1) dfs(grids, 0, j);
        if (grids[n-1][j] == 1) dfs(grids, n-1, j);
    }
     
    count = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grids[i][j] == 1) {
                dfs(grids, i, j);
            }
             
        }
    }
     
    cout << count << endl;
    return 0;
}

上面是代码随想录的版本，下面是我自己写的版本：

#include<iostream>
#include<vector>
using namespace std;
 
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
 
void dfs(vector<vector<int>>& grids, int x, int y) {
    if ( grids[x][y] == 0) return;
    grids[x][y] = 0;
     
    //标记当前遍历的岛屿不是孤岛
    if (x == 0 || x == grids.size()-1 || y == 0 || y == grids[0].size() -1) {
        count = -1;
    }
     
    //是孤岛才计数面积
    if (count != -1)
        count++;
     
     
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
         
        if (nextx < 0 || nextx >= grids.size() || nexty < 0 || nexty >= grids[0].size()) continue;
        dfs(grids, nextx, nexty);
 
    }
}
 
int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grids(n, vector<int>(m, 0));
     
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grids[i][j];
        }
    }
     
    int result = 0;
     
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grids[i][j] == 1) {
                count = 0;
                dfs(grids, i, j);
                //累加孤岛面积
                if (count > 0) result += count;
            }
             
        }
    }
     
    cout << result << endl;
    return 0;
}

广搜

代码如下：

#include<iostream>
#include<vector>
#include<queue>
using namespace std;

int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};

void bfs(vector<vector<int>>& grids, int x, int y) {
    queue<pair<int,int>> que;
    que.push({x, y});
    grids[x][y] = 0;
    count++;
    
    while (!que.empty()) {
        pair<int, int> cur = que.front();
        que.pop();
        int curx = cur.first;
        int cury = cur.second;
        for (int i = 0; i < 4; i++) {
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1];
            
            if (nextx < 0 || nextx >= grids.size() || nexty < 0 || nexty >= grids[0].size()) continue;
            if (grids[nextx][nexty] == 1) {
                que.push({nextx, nexty});
                grids[nextx][nexty] = 0;
                count++;
            }

        }
    }

}

int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grids(n, vector<int>(m, 0));
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grids[i][j];
        }
    }
    
    //将接触边缘的岛屿先标记成水
    //从左侧和右侧向中间遍历
    for (int i = 0; i < n; i++) {
        if (grids[i][0] == 1) bfs(grids, i, 0);
        if (grids[i][m-1] == 1) bfs(grids, i, m-1);
    }
    //从上面和下面向中间遍历
    for (int j = 0; j < m; j++) {
        if (grids[0][j] == 1) bfs(grids, 0, j);
        if (grids[n-1][j] == 1) bfs(grids, n-1, j);
    }
    
    count = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grids[i][j] == 1) {
                bfs(grids, i, j);
            }
            
        }
    }
    
    cout << count << endl;
    return 0;
}

二、102. 沉没孤岛

卡码网题目链接
文章讲解

思路：
一开始我也是想另外用一个visited数组来标记周边岛屿，但对比过代码随想录里的解法，代码随想录的更巧妙：

步骤一：深搜或者广搜将地图周边的 1 （陆地）全部改成 2 （特殊标记）

步骤二：将水域中间 1 （陆地）全部改成 水域（0）

步骤三：将之前标记的 2 改为 1 （陆地）
在这里插入图片描述
代码如下：

#include<iostream>
#include<vector>
using namespace std;

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};

void bfs(vector<vector<int>> &grids, int x, int y) {
    if (grids[x][y] == 0 || grids[x][y] == 2) return;
    grids[x][y] = 2;
    
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        
        if (nextx < 0 || nextx >= grids.size() || nexty < 0 || nexty >= grids[0].size()) continue;
        bfs(grids, nextx, nexty);
    }
}

int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grids(n, vector<int>(m, 0));
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grids[i][j];
        }
    }
    
    //将不是孤岛的岛屿标记成2
    // 从左侧边，和右侧边 向中间遍历
    for (int i = 0; i < n; i++) {
        if (grids[i][0] == 1) bfs(grids, i, 0);
        if (grids[i][m - 1] == 1) bfs(grids, i, m - 1);
    }
    // 从上边和下边 向中间遍历
    for (int j = 0; j < m; j++) {
        if (grids[0][j] == 1) bfs(grids, 0, j);
        if (grids[n - 1][j] == 1) bfs(grids, n - 1, j);
    }
    
    //将孤岛标记成0，将其他岛屿标记成1
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grids[i][j] == 1) grids[i][j] = 0;
            if (grids[i][j] == 2) grids[i][j] = 1;
        }
    }
    //打印结果
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cout << grids[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

三、103. 水流问题

卡码网题目链接
文章讲解

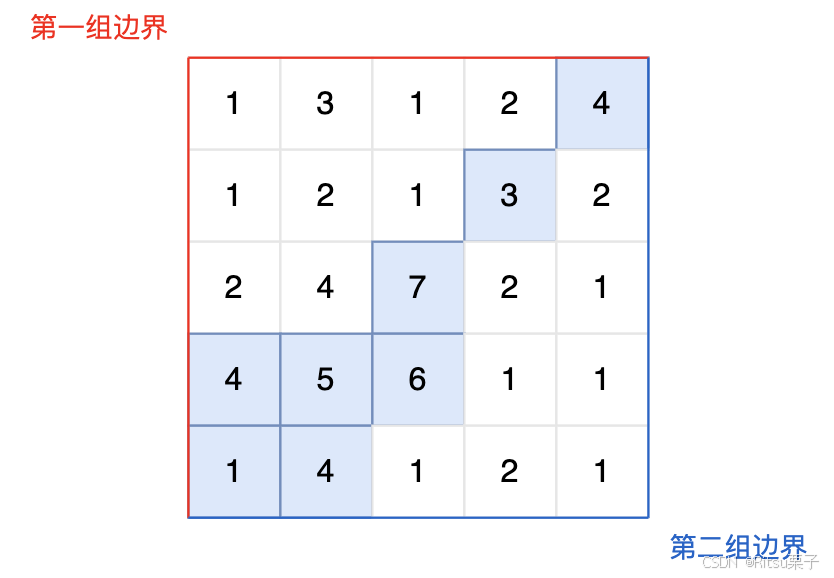
在这里插入图片描述
图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。

思路：
最直接的想法是遍历每个节点，然后用深搜或者广搜判断是否能到达第一组边界和第二组边界。但是会超时，遍历所有节点是mn，每个节点的深搜或者广搜都需要mn，那么时间复杂度就是m^2 *n^2了

那么反过来想，分别从第一组边界和第二组边界出发，能被两边标记到的节点，也就是能同时到达两组边界的节点。
在这里插入图片描述

代码如下：

#include <iostream>
#include <vector>
using namespace std;

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int n, m;
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
    if (visited[x][y]) return;

    visited[x][y] = true;

    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
        if (grid[x][y] > grid[nextx][nexty]) continue; // 注意：这里是从低向高遍历

        dfs (grid, visited, nextx, nexty);
    }
    return;
}

int main() {
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    
    // 标记从第一组边界上的节点出发，可以遍历的节点
    vector<vector<bool>> first(n, vector<bool>(m, false));
    // 标记从第一组边界上的节点出发，可以遍历的节点
    vector<vector<bool>> second(n, vector<bool>(m, false));
    
    // 从最上和最下行的节点出发，向高处遍历
    for (int i = 0; i < n; i++) {
        dfs(grid, first, i, 0); // 遍历最左列，接触第一组边界
        dfs(grid, second, i, m - 1); // 遍历最右列，接触第二组边界
    }
    
    // 从最左和最右列的节点出发，向高处遍历
    for (int j = 0; j < m; j++) {
        dfs(grid, first, 0, j); // 遍历最上行，接触第一组边界
        dfs(grid, second, n - 1, j); // 遍历最下行，接触第二组边界
    }
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            // 如果这个节点，从第一组边界和第二组边界出发都遍历过，就是结果
            if (first[i][j] && second[i][j]) cout << i <<  " " << j << endl;
        }
    }
    
    return 0;
    
}

四、104. 建造最大岛屿

卡码网题目链接
文章讲解

思路：
1.一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积
2.如果第一次遍历完发现整个地图都是陆地，直接返回全面积。
3.第二次遍历地图，遍历每格水，寻找当前节点邻近的岛屿，累加邻近岛屿面积（对于每格水，需要有一个set来存放已经遍历过的岛屿）
在这里插入图片描述

在这里插入图片描述

代码如下：

#include<iostream>
#include<vector>
#include<unordered_map>
#include<unordered_set>
using namespace std;

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int n, m;
int count;

void dfs(vector<vector<int>> &grid, vector<vector<bool>> &visited, int x, int y, int mark) {
    if (grid[x][y] == 0 || visited[x][y]) return; //终止条件，遇到水或者已经遍历过的陆地
    visited[x][y] = true;
    grid[x][y] = mark; //岛屿标记成相应的编号
    count++;
    
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
        dfs(grid, visited, nextx, nexty, mark);
    }
}

int main() {
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    
    vector<vector<bool>> visited(n, vector<bool>(m, false)); //标记访问过的点
    unordered_map<int,int> gridNum; //存储每个岛屿的面积
    bool isAllGrid = true; //标记是否整个地图都是陆地
    int mark = 2; //记录每个岛屿的编号
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 0) isAllGrid = false;
            if (!visited[i][j] && grid[i][j] == 1) {
                count = 0; //初始化每个岛屿的面积
                dfs(grid, visited, i, j, mark); //寻找相连的陆地部分
                gridNum[mark] = count; //记录每个岛屿的面积
                mark++;
            }
        }
    }
    
    //如果全是陆地，直接输出整个面积
    if (isAllGrid) {
        cout << n*m << endl;
        return 0;
    }
    
    int result = 0;
    unordered_set<int> visitedGrid; //标记访问过的岛屿
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            count = 1; //初始化岛屿面积，水变陆地的这格先加上
            visitedGrid.clear(); //每次遍历到新的一格水，清空之前累加过的岛屿
            //遍历每一格水，然后统计相邻的面积
            if (grid[i][j] == 0) {
                //遍历[i,j]四周的岛屿，统计总面积
                for (int k = 0; k < 4; k++) {
                    int neari = i + dir[k][0];
                    int nearj = j + dir[k][1];
                    
                    if (neari < 0 || neari >= n || nearj < 0 || nearj >= m) continue;
                    int markNum = grid[neari][nearj]; //岛屿的编号
                    if (visitedGrid.count(markNum)) continue; //已经统计过了的岛屿就跳过
                    count += gridNum[markNum]; //累加岛屿面积
                    visitedGrid.insert(markNum); //标记已经统计过该岛屿了
                }
            }
            result = max(count, result);
        }
    }
    
    cout << result << endl;
    
    return 0;
}

时间复杂度 n * n 。

总结

1.对于孤岛的处理，从四周先搜索挨着四周的岛屿。
2.如果求孤岛，先遍历四周将周边岛屿标记成0，再重新遍历地图，就剩下孤岛了；
3.如果求四周岛屿，先遍历四周将岛屿标记成2，再重新遍历地图，将孤岛沉没：1->0，四周岛屿标记回1：2->1。
4.水流问题，求水流能到达两个边界的节点，转化为从两个边界出发，两边都能到达的节点就是结果。
5.建造最大岛屿，第一次遍历用map存储每个岛屿的面积和编号，第二次遍历水节点，用bfs或者dfs寻找周边岛屿(用set存储找过的岛屿)，累加岛屿面积，求最大值。

明天继续加油！

Ritsu栗子
关注
代码随想录算法训练day59---图论系列4
qq_38365428的博客
02-20 691
今天是算法营的第59天，希望自己能够坚持下来！今天继续图论part！今日任务：● 110.字符串接龙● 105.有向图的完全可达性● 106.岛屿的周长字符串接龙 ：求最短路径，考虑用广搜。根据题意可知节点的连接是“只替换一个字符”，遍历字符串，再分别替换成26字母，并用set检查是否在list中。有向图的完全可达性：需要有一个数组来记录到达过的路径，注意这里不需要回溯。岛屿的最大面积：方法一：岛屿周围是水或者边界就是边长 方法二：周长= 岛屿数量4 - 相邻的岛屿数2。
代码随想录算法训练day57---图论系列2《岛屿问题》
qq_38365428的博客
02-09 798
今天是算法营的第57天，希望自己能够坚持下来！今天继续图论part！今日任务：● 99.岛屿数量 深搜● 99.岛屿数量 广搜● 100.岛屿的最大面积1.使用int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};来获取下一步的坐标2.深度优先搜索dfs的终止条件可以放在开头，也可以放在调用递归前，区别是对函数是处理本次节点还是下一个节点。3.广度优先搜索bfs，一旦加入队列就要标记。明天继续加油！
代码随想录算法训练day56---图论系列1
qq_38365428的博客
01-22 2529
今天是算法营的第32天，希望自己能够坚持下来！今日任务：● 62.不同路径● 63. 不同路径 II● 343. 整数拆分（思路较难）● 96. 不同的二叉搜索树（思路较难）动态规划的dp数组，通常二维的可以优化空间去掉dp[i]维度，但是不太好理解，遍历的时候也需要一些细节上的改动。明天继续加油！
【代码随想录训练营第42期 Day52打卡 - 岛屿问题2
记得要努力变强
09-06 1343
DFS--岛屿问题2
代码随想录day16--图论
weixin_42131601的博客
09-04 160
题目描述： 给定一个由 1（陆地）和 0（水）组成的矩阵，你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。 输入描述： 第一行包含两个整数 N, M，表示矩阵的行数和列数。 后续 N 行，每行包含 M 个数字，数字为 1 或者 0。 输出描述： 输出一个整数...
代码随想录day15--图论
weixin_34185396的博客
09-04 168
主要过程就是一圈一圈容器需要能保存所遍历过的元素：队列 ， 栈 ，数组队列：操作受限制的线性表，先进先出，一般应用的问题：速度不匹配，多用户竞争资源。顺序存储：头指针 front 指向对头元素，尾指针 rear 指向队尾元素的下一个位置。队列顺序存储的顺序存储类型的描述：登录后复制 #define MaxSize 50 ...
day-64 代码随想录算法训练营（19）图论 part 03
Ricardo的博客
10-02 478
827.最大人工岛 127.单词接龙 841.钥匙和房间
day-65 代码随想录算法训练营（19）图论 part 04
Ricardo的博客
10-05 755
463.岛屿的周长 1971.寻找图中是否存在路径 684.冗余连接 685.冗余连接 ||
代码随想录 day51 图论 1-6学习
qq_40445763的博客
07-15 251
【代码】代码随想录 day51 图论 1-6学习。
代码随想录训练营Day 67|卡码网110.字符串接龙、105.有向图的完全可达性、106.岛屿的周长
weixin_64434454的博客
06-23 725
思路：首先要知道 广搜只要搜到结果，这个结果的路径就是最短的。这道题正适合用广搜来解决。只要将一个元素添加进队列中，就对其进行访问标记。我们首先将对列的第一个元素取出，并将其路径加1。然后在这个字符串上进行改动，对每一位依次进行改动，可以将其遍历26个英文字母。如果改动后的字符串已经是结果字符串了，就将结果path+1进行输出；如果不是结果，就去看看这个改动后的字符串是否在字典里。如果在，就将其加入队列，并将其路径加1，进行访问标记。
【代码随想录day51】【C++复健】 101. 孤岛的总面积；102. 沉没孤岛； 103. 水流问题； 104. 建造最大岛屿
yumenohimiko的博客
12-07 799
此外，我还思考了下遍历边界的dfs和遍历中心的dfs是不是也需要不一样，但事实上用同一个就行了，不光消灭陆地，还要消灭孤岛，反正能统计出来数就完事了，我统计弹匣里发射出去的子弹数也不是相当于统计人数了。然后就去偷看了一下解析，发现卡哥做法就很单纯直接，虽然我找不到浮岛，但我可以把其他地方都换一个值，换完之后我再回来搞，你是2就换回1，你是1就置0，很简单直接的想法。当然我写的代码还是很麻烦的，不过毕竟图论是完全的一周目，能写出来就算万事大吉了，也不奢求什么代码行数上的提升了。
Day51 图论part02
2401_83448199的博客
12-24 422
另一种是for循环里面调用递归函数的时候，加上判断条件，这样递归函数里面传入的都是合法的节点，这样也就不用在写上终止条件了。3.整体思路就是如果是未被标记的陆地，result加1，然后把该节点加入到队列里面，然后做个标记，然后把该节点弹出，在以弹出的节点为中心，上下左右搜索合法的节点加入到队列里面。1.广搜的写法有一种会超时，如果从队列拿出节点，再去标记这个节点走过，会导致很多节点重复加入队列，相当于如果该节点符合要求，会被重复加入到队列里面，因为如果该节点不被弹出的话，是不会被标记的，这样就会导致超时。
代码随想录Day62 Floyd 算法精讲，A * 算法精讲 （A star算法），最短路算法总结篇，图论总结篇。
get_money_的博客
12-31 819
代码随想录Day62 Floyd 算法精讲，A * 算法精讲 （A star算法），最短路算法总结篇，图论总结篇。
HOT100 （哈希&双指针）
2301_80551759的博客
05-14 398
哈希&双指针
算法刷题-动态规划之区间DP
2301_81754159的博客
05-12 1098
今天是最后一天的区间dp，明天博主将给大家带来新的篇章。1.
LeetCode 513 找树左下角的值 LeetCode 112 路径总和 LeetCode106 从中序与后序遍历序列构造二叉树
weixin_59234335的博客
05-12 873
中序遍历 + 前序/后序遍历 可以 确定一个唯一的二叉树。必须有中序遍历的存在。而前序遍历+后序遍历无法确认。前序遍历：中左右后序遍历：左右中根据前序遍历和后序遍历的特性，我们只能唯一确定根节点，但无法从前序遍历和后序遍历划分出左右。例子如下：上面这两颗树的前序遍历都为[ 1, 2, 3] ，后序遍历为[3, 2, 1]
算法练习：19.JZ29 顺时针打印矩阵
最新发布
qq_34348690的博客
05-16 148
【代码】算法练习：19.JZ29 顺时针打印矩阵。
北斗导航 ｜ 接收机自主完好性监测算法综述，1980至2025年（原理，公式，代码）
尘世冰封的专栏
05-14 373
接收机自主完好性监测（RAIM）技术起源于20世纪80年代，最初为满足民航领域对卫星导航安全性的严苛需求而发展。国际民航组织（ICAO）要求CAT III类着陆系统的完好性风险需低于10⁻⁷/h。传统RAIM基于最小二乘残差法，通过冗余观测量（需至少5颗可见卫星）检测故障卫星，6颗以上可实现故障隔离（RAIM-FDE）。
力扣 旋转图像
fancy166166的博客
05-12 371
创建一个新的数组，存储旋转后的数组，将数组的第一行存到新创的数组空间的最后一列。
代码随想录算法训练营Day20
03-08
### 代码随想录算法训练营 Day20 学习内容与作业 #### 动态规划专题深入探讨 动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法[^1]。 #### 主要学习内容 - **背包问题系列** - ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值