代码随想录算法训练营day28

代码随想录算法训练营

—day28

---

前言

今天是算法营的第28天，希望自己能够坚持下来！
今日任务：
● 122.买卖股票的最佳时机II
● 55. 跳跃游戏
● 45.跳跃游戏II
● 1005.K次取反后最大化的数组和

---

一、122.买卖股票的最佳时机II

题目链接
文章讲解
视频讲解

思路：
计算相邻两天的利润，只收集正利润就是总的最佳收益

class Solution {
public:
    int maxProfit(vector<int>& prices) {
         int sum = 0;

        //计算相邻两天的利润，只收集正利润
         for (int i = 1; i < prices.size(); i++) {
            //if (prices[i] - prices[i - 1] > 0) sum += prices[i] - prices[i -1]; 
            sum += (max(prices[i] - prices[i - 1], 0)); //这种写法也是很妙，代替了if
         }

         return sum;
    }
};

---

二、55. 跳跃游戏

题目链接
文章讲解
视频讲解

思路：

1. 不需要具体去考虑跳到了那个元素底下，只需要统计最大的覆盖范围就可以了
2. 从0开始遍历覆盖范围cover，更新最大覆盖范围（当前元素能覆盖到的范围是i+nums[i]）
3. 如果cover覆盖到数组末尾了，说明能够跳到末尾。

代码如下：

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover = 0;
        if (nums.size() == 1) return true; //只有一个元素，就是能到达

        for (int i = 0; i <= cover; i++) { //注意这里是小于等于cover
            cover = max(i + nums[i], cover); //取当前覆盖范围和当前遍历元素可以跳跃的范围中最大值作为新的覆盖发哪位
            if (cover >= nums.size() - 1) return true; //说明覆盖范围到终点了，可以跳到终点
        }

        return false;
    }
};

---

三、跳跃游戏 II

题目链接
文章讲解
视频讲解

方法一

思路：
首先题目是默认都可以跳到末尾的，而求的是最少跳几次。
沿用上一题的覆盖的思想，但这道题遍历的是整个数组。
1.用next记录下一跳覆盖的最远下标，用cur记录本轮覆盖的最远下标
2.遍历数组，记录遍历过程中的最远下标（用于下一跳）
3.当遍历到本轮负该的最远下标，说明需要下一跳来增大覆盖距离了，此时result++并更新cur，cur = next;
4.当本轮最远下标大于等于数组末尾的时候，说明本轮可以到达末尾了，不需要再遍历（寻找下一跳最远下标）了，直接break。

代码如下：

class Solution {
public:
    int jump(vector<int>& nums) {
        if (nums.size() == 1) return 0;
        int result = 0; //记录要跳多少次
        int cur = 0; //当前覆盖的最远距离下标
        int next = 0; //下一跳覆盖的最远下标

        for (int i = 0; i < nums.size(); i ++) {
            next = max(i + nums[i], next); //遍历每一个下标，记录下一跳覆盖最远下标

            //当前已经遍历到本次最远距离的下标
            if (i == cur) {
                result++; //说明需要跳一下次
                cur = next; //更新当前覆盖最远距离下标
                if (cur >= nums.size() - 1) break; //当前覆盖最远距离已经到达终点，次数也在上面记录了，不需要再遍历了
            }
        }

        return result;
    }
};

方法二

因为题目是默认一定会跳到最后的，所以其实不需要判断最后一次的最远覆盖下标有没有超过数组末尾。
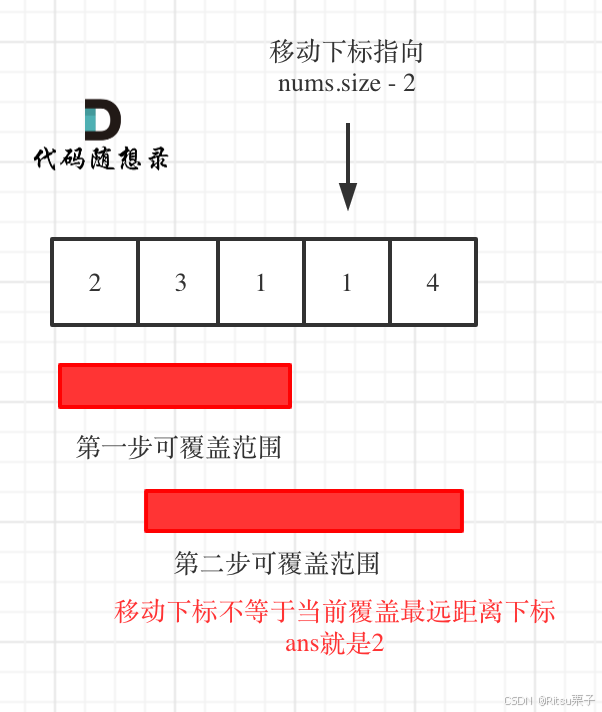
方法就是遍历的时候只遍历到倒数第二位，因为如果遍历到倒数第二位，

• i == cur的话，说明还差最后一跳就到末尾了，此时result++。
• i ！=cur的话，那么说明cur已经超过数组了，当前的result就是结果。

代码如下：

class Solution {
public:
    int jump(vector<int>& nums) {
        if (nums.size() == 1) return 0;
        int result = 0; //记录要跳多少次
        int cur = 0; //当前覆盖的最远距离下标
        int next = 0; //下一跳覆盖的最远下标

        for (int i = 0; i < nums.size() - 1; i ++) {
            next = max(i + nums[i], next); //遍历每一个下标，记录下一跳覆盖最远下标

            //当前已经遍历到本次最远距离的下标
            if (i == cur) {
                result++; //说明需要跳一下次
                cur = next; //更新当前覆盖最远距离下标
                // if (cur >= nums.size() - 1) break;  不需要判断了，因为遍历范围控制在了[0, nums.size()-1]，
            }
        }

        return result;
    }
};

---

1005. K 次取反后最大化的数组和

题目链接
文章讲解
视频讲解

思路：

1. 将数组按绝对值从大到小排列
2. 遍历数组，遇到负值的话就取反
3. 如果还有剩余的k，对绝对值最小的数进行取反（只需判断k是否为奇数，奇数只取反1次）
4. 最后遍历数组求和

代码如下：

class Solution {
//自定义比较函数，绝对值大的排前面
static bool cmp (int a, int b) {
    return abs(a) > abs(b);
}

public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end(), cmp); //将数组按照绝对值大小从大到小排序

        for (int i = 0; i < nums.size(); i++) { //遍历数组，如果是负数，则取反，k--
            if (nums[i] < 0 && k > 0) {
                nums[i] *= -1;
                k--;
            }
        }

        //如果k还没用完，判断k是否为奇数，奇数则取反最后一位绝对值最小的数
        if (k % 2 == 1) nums[nums.size() - 1] *= -1; 

        int result = 0;
        //遍历求和
        for (int num:nums) {
            result += num;
        }

        return result;
    }
};

---

总结

贪心算法第二天，依旧难的是思路，而且即使知道思路，代码中也有许多细节需要注意。

明天继续加油！