本文详细介绍了二叉查找树的实现，包括遍历、查找、插入和删除操作。接着讲解了平衡二叉树的概念，特别是右旋和左旋操作。最后，文章深入探讨了红黑树的特性，包括其五大性质和插入、删除操作对保持平衡的影响。
二叉树：用java基本代码可以表示为（掌握遍历算法 前序，中序，后序 熟练使用递归）
public
class TreeNode {
// 左节点
private TreeNode lefTreeNode;
// 右节点
private TreeNode rightNode;
// 当前结点的值
private int value;
TreeNode(int value){
this.value = value;
}
public TreeNode getLefTreeNode() {
return lefTreeNode;
}
public void setLefTreeNode(TreeNode lefTreeNode) {
this.lefTreeNode = lefTreeNode;
}
public TreeNode getRightNode() {
return rightNode;
}
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
}
二叉查找树
为了方便查找：实现二叉查找树，定义：当前根节点的左边全部比根节点小，当前根节点的右边全部比根节点大。
计算树的深度,只需求出左节点的树深度 和右节点的树深度 求其最大值
public int getHeight(TreeNode treeNode) {
if(treeNode == null) {
return 0;
} else {
int left = getHeight(treeNode.getLefTreeNode());
int right = getHeight(treeNode.getRightNode());
int max = left;
if(max < right) {
max = right;
}
return max+1;//表示加上当前结点，深度为1
}
}
二叉查找树的性质可以得出，从根节点一直往左走，直至无左路可走，即得最小元素；从根节点一直往右走，直至无右路可走，即得最大元素。对于二叉树查找出最大值：找出树左边最大值，找出树右边最大值，比较大小即可获取。
public int getMaxValue(TreeNode treeNode) {
if (treeNode == null) {
return 0;
} else {
int leftValue = getMaxValue(treeNode.getLefTreeNode());
int rightValue= getMaxValue(treeNode.getRightNode());
int max = treeNode.getValue();
if(max < leftValue) {
max = leftValue;
}
if(max < rightValue) {
max = rightValue;
}
return max;
}
}
二叉搜索树的插入：在treeNode中插入value，若value已存在则不变
public TreeNode addTreeNode(TreeNode treeNode,int value) {
if(treeNode == null) {
treeNode = new TreeNode(value);
return treeNode;
} else {
if(treeNode.getValue() > value) {
treeNode.setLefTreeNode(addTreeNode(treeNode.getLefTreeNode(),value));
} else if(treeNode.getValue() < value){
treeNode.setRightNode(addTreeNode(treeNode.getRightNode(),value));
}
return treeNode;
}
}
二叉搜索树的查找指定的值： 因为一棵由n个结点随机构造的二叉查找树的高度为lgn，所以顺理成章，二叉查找树的一般操作的执行时间为O(lgn)。但二叉查找树若退化成了一棵具有n个结点的线性链后，则这些操作最坏情况运行时间为O(n)。
public TreeNode getTreeNode(TreeNode treeNode,int value) {
if(treeNode == null) {
return null;
}else {
if(treeNode.getValue() == value){
return treeNode;
}
else if(treeNode.getValue() > value){
return getTreeNode(treeNode.getLefTreeNode(),value);
}else {
return getTreeNode(treeNode.getRightNode(),value);
}
}
}
5.二叉查找树的删除：
删除是二叉查找树中最为复杂的一个操作，可以分成三种情况来考虑：
①若是叶子节点的话，只需要将其赋值为空即可；
②若仅包含左节点或者右节点，则将其左节点或者右节点的值赋给其本身，将左右节点赋值为空；
③若既包含左节点，也包含右节点，则可以通过中序遍历将其前驱（或后继）节点的值赋给其本身，将前驱（后继）
节点删除。
/**
* @param tree
* @param value
*/
public void deleteTreeNode(TreeNode tree,int value) {
if(tree == null) {
return ;
}
TreeNode nodeValue = getTreeNode(tree,value);
if(nodeValue == null) {
return ;
}
if(nodeValue.getLefTreeNode() ==null && nodeValue.getLefTreeNode() ==null ) {
nodeValue = null;
} else if(nodeValue.getLefTreeNode() !=null && nodeValue.getLefTreeNode() ==null ) {
nodeValue = nodeValue.getLefTreeNode() ;
} else if (nodeValue.getLefTreeNode() ==null && nodeValue.getLefTreeNode() !=null) {
nodeValue = nodeValue.getLefTreeNode() ;
} else {
//找出左节点中的最大值，并将该值设为当前节点值
nodeValue.setValue(getMaxValue(nodeValue.getLefTreeNode()));
//删除相应的 前驱值的节点
deleteTreeNode(nodeValue.getLefTreeNode(),nodeValue.getValue());
}
}
package tree;
/**
* 二叉查找树
*/
public class SearchTree<V extends Comparable> {
Node<V> head;
// 二叉查找树
public void add(V value){
Node<V> node;
if (head == null) {
head = new Node<>(value);
} else {
node = head;
add(node, value);
}
}
private Node add(Node<V> node, V value) {
if (node == null) {
node = new Node<>(value);
} else {
if (node.value.compareTo(value) > 0) {
node.left = add(node.left, value);
} else if (node.value.compareTo(value) < 0){
node.right = add(node.right, value);
}
}
return node;
}
/**
* 二叉查找
*/
public Node getNode(V v) {
return getNode(head, v);
}
public Node getNode(Node<V> node, V value) {
if (node == null) {
return node;
}
if (node.value.compareTo(value) > 0) {
return getNode(node.left, value);
} else if (node.value.compareTo(value) == 0){
return node;
} else {
return getNode(node.right, value);
}
}
public void delete(V value) {
delete(head, value);
}
private void delete(Node<V> node, V value) {
if (node == null) {
return;
}
// 找出对应的节点,若不存在则删除
Node<V> valueNode = getNode(value);
if (valueNode == null) {
return;
}
// 若存在
// 1若为叶子节点 直接删除
if (valueNode.left == null && valueNode.right == null) {
valueNode = null;
} else if (valueNode.left == null) {
//2 若只存在右节点
valueNode = valueNode.right;
} else if (valueNode.right == null) {
// 若只存在左节点
valueNode = valueNode.left;
} else {
// 3若左右节点都存在
// 找出左节点中的 最大值，并讲当前值设置为对应的最大值
valueNode.value = getMaxNode(valueNode.left);
// 同时删除 该节点左节点中原先的该最大值节点
delete(valueNode.left, valueNode.value);
}
}
// 找出最大值
public V getMaxNode(Node<V> node) {
if (node == null) {
return null;
} else {
V leftMax = getMaxNode(node.left);
V rightMax =getMaxNode(node.right);
V max = node.value;
if (leftMax == null || max.compareTo(leftMax) > 0) {
max = leftMax;
}
if (rightMax == null || max.compareTo(rightMax) > 0) {
max = rightMax;
}
return max;
}
}
// 静态内部类修饰节点
static class Node<V>{
V value;
Node<V> left;
Node<V> right;
Node(V v) {
this.value = v;
}
}
}
这里再额外扩展一种类型：平衡二叉树
通过每个节点加上平衡因子，每个节点的平衡因子必须为 0，1，-1中的一种（平衡因子为该节点左子树的高度减去右子树的高度）来保证高度平衡
其中插入时候保证平衡运用了：简单左旋，简单右旋，左旋加右旋，右旋加左旋。
右旋：当插入项为最近的平衡因子为+2的祖先（A）的左孩子（B）的左子树中。（令A的父亲指向B，A的左链等于B的右链，B的右链指向A，以下图为需要右旋的图列）
A B
B C D A
D E F E C
F
左旋：当插入项为最近的平衡因子为-2的祖先的右孩子的右子树中。(令A的父亲指向C，A的右链等于C的左链，C的左链指向A)
A
B C
D E
F
左右旋：当插入项为最近的平衡因子为+2的祖先的左孩子的右子树中。
右左旋：当插入项为最近的平衡因子为-2的祖先的右孩子的左子树中。
红黑树
一种二叉查找树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。
红黑树虽然本质上是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
为保证自横性质，最长路径不超过最短路径的2倍，具有以下5大性质：
（1）根节点是黑 （根节点 即表示起点）
（2） 节点为红色或黑色
（3）每个叶子结点都是黑色的空节点 NIL（一棵树当中没有子结点（即度为0）的结点称为叶子结点）
（4） 每个红色节点的子节点都是黑色
（5） 从任意节点到其 每个叶子 的所有路径 都包含相同数目的黑色节点（在进行红黑树的构造的时候，为了此性质，则必须每次插入的节点颜色预设为红色，插入后，有可能会导致3、4不满足，然后进行节点调整。所以如果是构造出来的，一般来说，不会有节点全黑的红黑树）
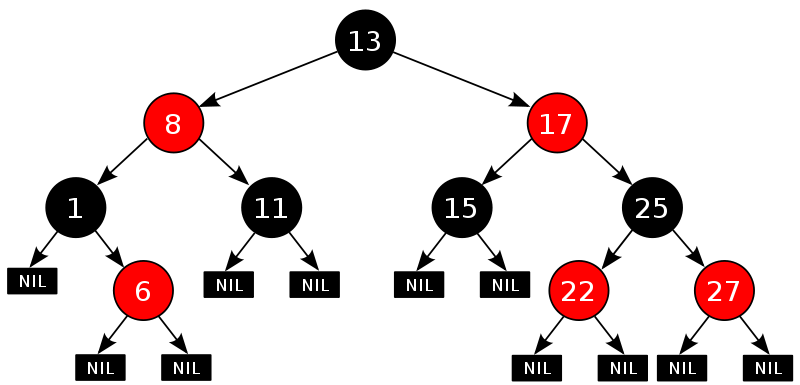
因为每一个红黑树也是一个特化的二叉查找树，因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而，在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。虽然插入和删除很复杂，但操作时间仍可以保持为O(log n) 次。
左旋
逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子。
右旋
顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子
扫一扫
1570
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
