最大堆和最大索引堆

最大堆是一种常用的数据结构，它可以快速的得到堆中最大的元素，比如在计算机执行多线程的是够，我们可以快速得到优先级最大的进行并对其优先执行，并且可以对剩余的线程快速进行排序，堆顶的元素又是优先级最大的那个子线程。依靠最大堆的这个特性，我们可以动态的调整线程的优先级并且快速索引到优先级最高的子线程。

作为一个数据结构，其基本的操作莫过于添加元素和删除元素了。在向堆中添加元素的同时需要进行shift up操作，将该元素放到合适的位置上；当删除元素的时候，我们首先将堆顶元素保存在item中，然后将堆顶元素用堆尾元素替换并更新堆元素可访问的范围，最后再对堆顶元素进行shift down操作，将无序的数组更新成最大堆的形式。关于shift up和shift down的详细介绍，可以看一下我的上一篇博客。

1. 最大堆

相关代码如下：

#pragma once
#ifndef _MAXHEAP_H_
#define _MAXHEAP_H_
 
template<typename Item>
class MaxHeap {
private:
	Item *data;
	int count;
	int capacity;
 
public:
	MaxHeap(int capacity);
	~MaxHeap();
	bool isEmpty();
	bool isFull();
	int size();
	bool insert(Item item);
	// 删除堆顶元素，并将堆顶元素保存在item中
	bool deleteItem(Item &item);
	void show();
 
// 私有成员函数
private:
	void shiftUp(const int index);
	void shiftDown(const int k);
};
 
/* -------------------------------------------------- */
// 构造函数和析构函数
template<typename Item>
MaxHeap<Item>::MaxHeap(int c) {
	capacity = c;
	count = 0;
	data = new Item[capacity + 1];
}
 
template<typename Item>
MaxHeap<Item>::~MaxHeap() {
	capacity = 0;
	count = 0;
	delete[] data;
}
 
// 判断堆是否为空
template<typename Item>
bool MaxHeap<Item>::isEmpty() {
	return 0 == count;
}
 
// 判断堆是否满了
template<typename Item>
bool MaxHeap<Item>::isFull() {
	return count == capacity;
}
 
// 返回堆中数据的数量
template<typename Item>
int MaxHeap<Item>::size() {
	return count;
}
 
// 私有成员函数：对某个位置的数据进行shift up
template<typename Item>
void MaxHeap<Item>::shiftUp(const int index) {
	// i表示要插入的位置
	int i = index;
	// 保存首个元素
	Item temp = data[index];
	while (i > 1 && data[i / 2] < temp) {
		data[i] = data[i / 2];
		i /= 2;
	}
	data[i] = temp;
}
 
// 向队列中插入数据
template<typename Item>
bool MaxHeap<Item>::insert(Item item) {
	if (count >= capacity)
		return false;
	// 向堆中插入数据，索引从1开始
	data[++count] = item;
	shiftUp(count);
}
 
// 打印整个堆
template<typename Item>
void MaxHeap<Item>::show() {
	for (int i = 1;i <= count;i++)
		std::cout << data[i] << " ";
	std::cout << std::endl;
}
 
template<typename Item>
void MaxHeap<Item>::shiftDown(const int k) {
	int index = k;
	Item temp = data[k];
	int flag;
	// 如果存在左节点才进行交换
	while (2 * index <= count) {
		// 默认需要交换的索引是左节点的索引
		flag = 2 * index;
		// 如果存在右节点，并且右节点的值比左节点大
		if (flag + 1 <= count&&data[flag] < data[flag + 1])
			flag += 1;
		// 如果要比较的结点比父节点小，就退出
		if (data[flag] <= temp)
			break;
		data[index] = data[flag];
		index = flag;
	}
	data[index] = temp;
}
 
// 删除堆顶元素
template<typename Item>
bool MaxHeap<Item>::deleteItem(Item &item) {
	if (isEmpty())
		return false;
	item = data[1];
	// 将最后一个元素放到首个元素，并进行shiftDown
	data[1] = data[count--];
	// 当堆中元素的个数多于一个的时候才进行shiftdown操作
	if (count >= 2)
		shiftDown(1);
	return true;
}
 
#endif // !_MAXHEAP_H_

 

2. 最大索引堆

在最大堆中，如果data数组中存放着内存较大的数据类型，比如结构体或者类对象，在shift down和shift up中频繁用到的复制操作显然会增加更长的时间；亦或者，当我们并不想改变data中数据的位置，但是还需要能够快速得到data中最大元素，该如何处理呢？可以让最大堆的结点保存着data数据的索引，这就是最大索引堆的概念。

也就是说，最大堆的节点保存和data的元素；最大索引堆的节点保存着data的索引。因此，我们可以另外开辟一块内存空间indexArray，其中保存着data的索引，而节点就保存着indeArray中的元素。因此，shift down和shift up中数据比较的准则就变成了：比较data数据，但是却交换indexArray的元素。

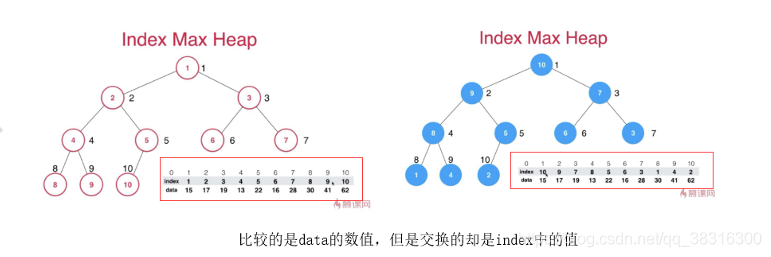
最大索引堆的场景多用于动态调整，比如当我们改变了data数组某个位置元素的值，我们依然要保证改变之后依然还是一个最大索引堆。在最大堆中，这个问题很好处理，比如我们将data[3]改成100，我们只需要对结点3依次进行shift down和shift up操作；而在索引堆中，因此结点中保存着index数组的元素，而我们只知道data的索引以及修改之后元素的值，怎么根据data的索引得到index在结点中的索引呢？只要知道了在结点中的索引，我们再依次进行shift down和shift up操作就可以将改变之后的堆更新成最大索引堆了。现在问题来到了：如果根据data的索引得到其在结点中索引？

我们可以另外添加一个数组reverseArray，其保存着data的索引在结点中索引位置，比方说reverseArray[0] = 2，这就表示data[0]在结点中索引位置是2；而indexArray数组就表示这每个结点所代表的data元素的索引，biang说indexArray[2] = 0，这就表示这结点2中的保存着data[0]的元素。由此可见reverseArray数组和indexArray表示的函数是不是正好相反呢？

0	1	2	3	4	5	6	7	8	9	10
data	15	17	19	13	22	16	28	30	41	62
index	10	9	7	8	5	6	3	1	4	2
reverse	8	10	7	9	5	6	3	4	2	1

因此，我们就可根据reverseArray得到data元素在结点中的位置了，在写代码的时候凡是对indexArray进行改变的时候，就需要相应的改变reverseArray数组的值。修改的原则参考下面的规则：

比方说，当交换index[1]和index[9]的时候，我们需要reverse[index[1]]和reverse[index[9]]的位置，也就是将reverse[index[1]] 更新成1，将reverse[index[9]]更新成9，因为上面的那个规律是一直存在的。

因此，最大索引堆的相关代码就可以这样来写

#pragma once
#ifndef _INDEXMAXHEAP_H_
#define _INDEXMAXHEAP_H_


// 模板类的声明和定义要放在一起
template<class Item>
class IndexMaxHeap {
private:
	// 保存数据的媒介
	Item *dataArray;
	// 保存索引的媒介
	int *indexArray;
	// 保存每个data数据的索引在结点中的位置索引
	int *reverseArray;
	// 当前数组中有多少元素
	int count;
	// 最大索引堆可存放元素的数量
	int capacity;

public:
	// 构造函数和析构函数
	IndexMaxHeap(const int cap);
	~IndexMaxHeap();
	// 最大索引堆是否为空
	bool isEmpty();
	// 最大索引堆是否满了
	bool isFull();
	// 返回堆中有多少元素
	int size();
	// 向堆中插入数据
	bool insertItem(const Item item);
	// 从堆中删除数据，并保存在item中
	bool deleteItem(Item & item);
	// 获得最大元素，并将最大元素保存在item中
	bool getMaxItem(Item &item);
	// 获取最大元素的索引，并将索引保存在i中
	bool getMaxIndex(int &i);
	// 改变dataArray中某个结点的值，使其变成item
	bool change(const int i, const Item item);
	// 打印最大堆中的数据
	void show();
	void showInfo();

	// 私有成员函数
private:
	void shiftUp(int i);
	void shiftDown(int i);

};

// 最大索引堆的实现
/*操作： 最大索引堆的构造函数*/
/*结果： 初始化最大索引堆的成员变量*/
template<class Item>
IndexMaxHeap<Item>::IndexMaxHeap(const int cap) {
	// 为数据数组和索引数组分配内存空间，因为是从1开始索引的
	// 因此需要开辟的空间需要新增加一位
	dataArray = new Item[cap + 1];
	indexArray = new int[cap + 1];
	reverseArray = new int[cap + 1];
	capacity = cap;
	count = 0;
}


/*操作： 最大索引堆的析构函数*/
/*结果： 释放相关内存*/
template<class Item>
IndexMaxHeap<Item>::~IndexMaxHeap() {
	count = 0;
	capacity = 0;
	delete[] dataArray;
	delete[] indexArray;
	delete[] reverseArray;
}


/*操作： 判断最大索引堆是否为空*/
/*结果： 如果最大索引堆为空，返回true；否则，返回false*/
template<class Item>
bool IndexMaxHeap<Item>::isEmpty() {
	return 0 == count;
}

/*操作： 判断最大索引堆是否满了*/
/*结果： 如果满了，返回true；否则，返回false*/
template<class Item>
bool IndexMaxHeap<Item>::isFull() {
	return count == capacity;
}

/*操作： 返回最大索引堆中数据的个数*/
/*结果： 返回当前堆中有多少元素*/
template<class Item>
int IndexMaxHeap<Item>::size() {
	return count;
}

/*操作： 向最大索引堆中添加元素*/
/*结果： 如果插入成功，返回true；否则，返回false*/
template<class Item>
bool IndexMaxHeap<Item>::insertItem(const Item item) {
	if (isFull())
		return false;
	dataArray[++count] = item;
	indexArray[count] = count;
	reverseArray[indexArray[count]] = count;
	// 通过shift up将末尾数据移动到最大堆中合适的位置
	shiftUp(count);
	return true;
}

/*操作：shift up将某个元素从底部向上移动到最大索引堆中合适的位置*/
/*结果：没有返回值，只是将第i个元素从顶部移动到最大堆中合适的位置*/
template<class Item>
void IndexMaxHeap<Item>::shiftUp(int i) {
	int temp = indexArray[i];
	// i表示可以插入的位置
	while (i > 1 && dataArray[indexArray[i / 2]] < dataArray[temp]) {
		indexArray[i] = indexArray[i / 2];
		reverseArray[indexArray[i]] = i;
		//reverseArray[indexArray[i / 2]] = i / 2;
		i /= 2;
	}
	indexArray[i] = temp;
	reverseArray[indexArray[i]] = i;
}

/*操作：删除最大索引堆中最大的元素*/
/*结果： 如果删除成功，返回true；如果失败，就返回false*/
template<class Item>
bool IndexMaxHeap<Item>::deleteItem(Item & item) {
	if (isEmpty())
		return false;
	// 首先需要将首个元素保存在item中，然后再将尾部元素移动到顶部，并更新count的值
	// dataArray其实并不需要进行任何改变，从头到尾只需要更新indexArray数组
	item = dataArray[indexArray[1]];
	indexArray[1] = indexArray[count--];
	// 对根结点进行shift down操作
	shiftDown(1);
}


/*操作：shift down将某个元素从顶部向下移动到最大堆中合适的位置*/
/*结果：没有返回值，只是将某个元素向下移动到合适的位置*/
template<class Item>
void IndexMaxHeap<Item>::shiftDown(int i) {
	// 设置一个变量来保存左右结点中最大结点的索引
	int maxIndex = i;
	// 使用一个变量来保存indexArray中第i个元素
	int temp = indexArray[i];
	// 如果存在左节点，就进行比较
	while (2 * i <= count) {
		maxIndex = i;
		// 如果存在右节点，并且右节点的值比左节点的大，就更新maxIndex的值
		if (2 * i + 1 <= count && dataArray[indexArray[2 * i + 1]] > dataArray[indexArray[2 * i]])
			maxIndex = 2 * i + 1;
		// 如果temp比最大结点都大的话，就退出
		if (dataArray[temp] >= dataArray[indexArray[maxIndex]])
			break;
		// 否则就更新indexArray的数据和i的值
		indexArray[i] = indexArray[maxIndex];
		reverseArray[indexArray[i]] = i;
		//reverseArray[indexArray[maxIndex]] = maxIndex;
		i = maxIndex;
	}
	indexArray[i] = temp;
	reverseArray[indexArray[i]] = i;
}


/*操作： 得到最大值的在dataArray中的索引*/
/*结果： 如果成功，就返回true；否则返回false*/
template<class Item>
bool IndexMaxHeap<Item>::getMaxItem(Item & item) {
	if (isEmpty())
		false;
	item = dataArray[indexArray[1]];
	return true;
}

/*操作： 得到最大值的索引*/
/*结果： 如果成功，就返回true，并将索引保存在i中；否则返回false*/
template<class Item>
bool  IndexMaxHeap<Item>::getMaxIndex(int &i) {
	if (isEmpty())
		return false;
	i = indexArray[1];
	return true;
}

/*操作： 改变data数组中某个索引的值*/
/*条件： i的索引是从0开始的，而data的索引是从1开始的*/
/*结果： 如果成功改变返回false，否则返回false*/
template<class Item>
bool IndexMaxHeap<Item>::change(const int i, const Item item) {
	// 在这边只根据data的索引进行修改
	dataArray[i + 1] = item;
	cout << "reverseArry[i+1] = " << reverseArray[i + 1] << endl;
	shiftDown(reverseArray[i + 1]);
	shiftUp(reverseArray[i + 1]);
	return true;
}

/*操作： 打印最大索引堆中的数据*/
/*结果： 按照索引数组的内容，依次打印最大索引堆中的内容*/
template<class Item>
void IndexMaxHeap<Item>::show() {
	for (int i = 1; i <= count;i++)
		cout << dataArray[indexArray[i]] << " ";
	cout << endl;
}


#endif // !_INDEXMAXHEAP_H_