本专栏按照 https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html 顺序进行总结 。
原理解析
基于值 的RL的缺陷
基于价值的深度强化学习方法有它自身的缺点,主要有以下三点:
- 基于价值的强化学习无法很好的处理连续空间的动作问题,或者时高维度的离散动作空间,因为通过价值更新策略时是需要对每个动作下的价值函数的大小进行比较的,因此在高维或连续的动作空间下是很难处理的。
- 在基于价值的强化学习中我们用特征来描述状态空间中的某一状态时,有可能因为个体观测的限制或者建模的局限,导致真实环境下本来不同的两个状态却再我们建模后拥有相同的特征描述,进而很有可能导致我们的value Based方法无法得到最优解。如下图:

当有些个体选择比较容易观测的特征来描述状态空间时,比如颜色,则在上图中两个灰色格子(代表着两个不同的状态)的特征表示是一样的,倘若我们的最终目的是要获得金币,则当你在左边的灰色格子时,你需要往右移;当你在右边的灰色格子时,你需要往左移。而在基于价值的强化学习方法中,策略往往时确定的,也就是你的状态确定了,动作就确定了,那么在这里如果两个灰色格子的状态是一样,则执行的动作是一样的。这显然是不行的。 - 无法解决随机策略问题,基于价值的强化学习的策略是确定的(当然也可以用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy,但是随机性没那么强),而基于策略的强化学习是具有随机性的。
策略梯度
首先,回顾一下策略梯度的思想:
- 先找到一个评价指标 J ( θ ) J(\theta) J(θ) (比如期望回报), θ \theta θ 是关于策略的参数。
- 使用随机梯度上升法
θ
=
θ
+
α
∇
θ
J
(
θ
)
\theta = \theta + \alpha \nabla_{\theta}J(\theta)
θ=θ+α∇θJ(θ) 来更新策略参数,从而不断的最大化评价指标;
- 这里核心的问题是估计这个梯度。我们需要找到一种采样方式,使得通过采样样本估计的梯度的期望正比于真实的梯度。
- 为什么采样梯度只需要正比于真实的梯度呢?这是因为在梯度上升中有一个步长因子,所以即使采样梯度是真实梯度的很多倍,也可以通过步长因子缩放回来。
- 策略梯度表明:
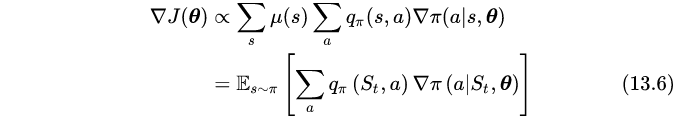
- 其中, π θ \pi_\theta πθ 指的是给定参数 θ \theta θ 下的 策略 π \pi π
- μ π ( s ) \mu_\pi(s) μπ(s) 指的是 在策略 π \pi π 下任意时间 t t t 状态 s s s 出现的期望
- 下面那个式子理解为 一个episode 的 平均梯度
- 上式中我们把对状态 s s s 的求和操作变成了期望操作。这样就得到了我们需要的一个采样量,它的期望等于真实的梯度。(13.6) 刚好是要给期望形式,它说明这个采样值就是 ∑ a q π ( S t , a ) ∇ π ( a ∣ S t , θ ) \sum_{a} q_\pi(S_t, a)\nabla_\pi(a|S_t,\theta) ∑aqπ(St,a)∇π(a∣St,θ)
- 那么依照SGA(随机策略上升),就可以构造如下的算法:

- 其中 q ^ \hat q q^ 是 q π q_\pi qπ 的近似值。这个方法叫做 all-actions 方法。因为梯度更新中考虑了所有的动作。
- 对于式中 q π ( S t , a ) q_\pi(S_t, a) qπ(St,a) 的不同改进形成了各种算法
蒙特卡罗策略梯度REINFORCE算法
对于REINFORCE,则是policy-gradient methods下的一个具体算法:
-
每次sample一个episode然后对参数进行更新:REINFORCE中利用当前episode的return: G t = ∑ k = t + 1 T γ k − t R k G_t = \sum\limits_{k=t+1}^T \gamma^{k-t}R_k Gt=k=t+1∑Tγk−tRk 作为 q π ( S t , A t ) q_\pi(S_t,A_t) qπ(St,At) 对 θ \theta θ 进行更新;下面是推导过程。
-
根据上述策略梯度公式 (13.7)的推导,这个方法叫做 all-actions 方法。而经典的REINFORCE算法在每个更新中只考虑一个实际采取的动作 A t A_t At 。即把动作求和也变成期望,如下:

- 有了个这个形式,就得到另一个SGA的更新表达式,如下:

这就是REINFORCE算法。利用 ∇ l n x = ∇ x / x \nabla lnx = \nabla x /x ∇lnx=∇x/x,上式可以简写为:

- 如果 G t G_t Gt 大于零,参数更新的方向会增加它在当前状态的概率。意思就是如果回报是有利的,就增加这个动作出现的概率。并且回报越大,梯度更新的幅度越大,概率增加的也就越大。另外利用 E π [ G t ∣ S t , A t ] = q π ( S t , A t ) E_\pi[G_t|S_t,A_t]= q_\pi(S_t, A_t) Eπ[Gt∣St,At]=qπ(St,At) 我们把 q q q 换成了 G t G_t Gt ,表示 t t t 时刻后回报总和。是通过蒙特卡洛的方式计算的。所以REINFORCE是个基于MC的算法。
- 有了个这个形式,就得到另一个SGA的更新表达式,如下:
REINFORCE简单的扩展:REINFORCE with baseline
利用了等式 :
也就是说可以在
q
π
(
S
t
,
A
t
)
q_\pi(S_t,A_t)
qπ(St,At) 后减去任意与动作
a
a
a 无关的项
b
(
s
)
b(s)
b(s) ,这样可以减少算法的variance;
更新项就变成了:

另外,简单说一下:
REINFORCE利用的是Monte Carlo的思想,如果改用Temporal Difference思想的话我们就可以得到Actor Critic。
- 将REINFORCE中更新时使用的 G t G_t Gt 改为 R t + 1 + γ v ^ ( S t + 1 ) − b ( S t ) R_{t+1} + \gamma \hat v(S_{t+1}) -b(S_t) Rt+1+γv^(St+1)−b(St),其中其中 v ^ ( s ) \hat v(s) v^(s) 是我们对状态值函数的估计,一般我们可以直接用 v ^ ( S t ) \hat v(S_t) v^(St) 来确定 b ^ ( S t ) \hat b(S_t) b^(St);
- 最后我们的更新式变成了:

当然由于Actor Critic是Temporal Difference的思想,所以在更新的时候可以在线更新
借用一下网友的总结:
- Policy Gradient分两大类:基于Monte-Carlo的REINFORCE(MC PG)和基于TD的Actor Critic(TD PG)。
- REINFORCE是Monte-Carlo式的探索更新,也就是回合制的更新,至少要等一个回合结束才能更新policy;
- 而Actor Critic是基于TD的,也就是说可以按step来更新,不需要等到回合结束,是一种online learning。
- MC PG不利用马尔可夫性,TD PG利用马尔可夫性。
算法实现
总体流程
function REINFORCE
initialise θ arbitrarily
for each episode {s1, a1, r2, ...,s{T-1}, a_{T-1},r_T} ~ π_θ do
for t=1 to T-1 do
θ = θ + α ▽θ log π_θ(st,at)vt
end for
end for
return θ
end function
代码实现
- 离散动作
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.nn.utils as utils
import torchvision.transforms as T
from torch.autograd import Variable
import pdb
class Policy(nn.Module):
def __init__(self, hidden_size, num_inputs, action_space):
super(Policy, self).__init__()
self.action_space = action_space
num_outputs = action_space.n
self.linear1 = nn.Linear(num_inputs, hidden_size)
self.linear2 = nn.Linear(hidden_size, num_outputs)
def forward(self, inputs):
x = inputs
x = F.relu(self.linear1(x))
action_scores = self.linear2(x)
return F.softmax(action_scores) # 输出动作的softmax分布
class REINFORCE:
def __init__(self, hidden_size, num_inputs, action_space):
self.action_space = action_space
self.model = Policy(hidden_size, num_inputs, action_space)
self.model = self.model.cuda()
self.optimizer = optim.Adam(self.model.parameters(), lr=1e-3)
self.model.train()
def select_action(self, state):
probs = self.model(Variable(state).cuda())
action = probs.multinomial().data
prob = probs[:, action[0,0]].view(1, -1)
log_prob = prob.log()
entropy = - (probs*probs.log()).sum()
return action[0], log_prob, entropy
def update_parameters(self, rewards, log_probs, entropies, gamma):
R = torch.zeros(1, 1)
loss = 0
for i in reversed(range(len(rewards))):
R = gamma * R + rewards[i]
loss = loss - (log_probs[i]*(Variable(R).expand_as(log_probs[i])).cuda()).sum() - (0.0001*entropies[i].cuda()).sum()
loss = loss / len(rewards)
self.optimizer.zero_grad()
loss.backward()
utils.clip_grad_norm(self.model.parameters(), 40)
self.optimizer.step()
- 连续动作
import sys
import math
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.nn.utils as utils
import torchvision.transforms as T
from torch.autograd import Variable
pi = Variable(torch.FloatTensor([math.pi])).cuda()
def normal(x, mu, sigma_sq):
a = (-1*(Variable(x)-mu).pow(2)/(2*sigma_sq)).exp()
b = 1/(2*sigma_sq*pi.expand_as(sigma_sq)).sqrt()
return a*b
class Policy(nn.Module):
def __init__(self, hidden_size, num_inputs, action_space):
super(Policy, self).__init__()
self.action_space = action_space
num_outputs = action_space.shape[0]
self.linear1 = nn.Linear(num_inputs, hidden_size)
self.linear2 = nn.Linear(hidden_size, num_outputs)
self.linear2_ = nn.Linear(hidden_size, num_outputs)
def forward(self, inputs):
x = inputs
x = F.relu(self.linear1(x))
mu = self.linear2(x)
sigma_sq = self.linear2_(x)
return mu, sigma_sq
class REINFORCE:
def __init__(self, hidden_size, num_inputs, action_space):
self.action_space = action_space
self.model = Policy(hidden_size, num_inputs, action_space)
self.model = self.model.cuda()
self.optimizer = optim.Adam(self.model.parameters(), lr=1e-3)
self.model.train()
def select_action(self, state):
mu, sigma_sq = self.model(Variable(state).cuda())
sigma_sq = F.softplus(sigma_sq)
eps = torch.randn(mu.size())
# calculate the probability
action = (mu + sigma_sq.sqrt()*Variable(eps).cuda()).data
prob = normal(action, mu, sigma_sq)
entropy = -0.5*((sigma_sq+2*pi.expand_as(sigma_sq)).log()+1)
log_prob = prob.log()
return action, log_prob, entropy
def update_parameters(self, rewards, log_probs, entropies, gamma):
R = torch.zeros(1, 1)
loss = 0
for i in reversed(range(len(rewards))):
R = gamma * R + rewards[i]
loss = loss - (log_probs[i]*(Variable(R).expand_as(log_probs[i])).cuda()).sum() - (0.0001*entropies[i].cuda()).sum()
loss = loss / len(rewards)
self.optimizer.zero_grad()
loss.backward()
utils.clip_grad_norm(self.model.parameters(), 40)
self.optimizer.step()








 本文深入探讨了策略梯度算法的基础原理,分析了基于值的强化学习方法的局限性,并详细介绍了蒙特卡罗策略梯度(REINFORCE算法)及其扩展REINFORCE with baseline的工作机制。此外,还提供了算法的具体实现代码。
本文深入探讨了策略梯度算法的基础原理,分析了基于值的强化学习方法的局限性,并详细介绍了蒙特卡罗策略梯度(REINFORCE算法)及其扩展REINFORCE with baseline的工作机制。此外,还提供了算法的具体实现代码。
















 655
655

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








