STL 栈与队列

最新推荐文章于 2024-05-27 23:02:29 发布

原创最新推荐文章于 2024-05-27 23:02:29 发布 · 373 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#STL #数据结构 #简单计算器 #表达式求值

数据结构同时被 3 个专栏收录

21 篇文章

订阅专栏

队列

4 篇文章

订阅专栏

栈

3 篇文章

订阅专栏

STL 栈与队列

关于栈的理解： 后进先出（Last In First Out）简称为LIFO线性表。          限定插入和删除数据元素的操作只能在线性表的一端进行(这一端被称为栈顶，相对地，把另一端称为栈底。) 向一个栈插入新元素又称作 进栈、入栈或压栈，它是把新元素放到栈顶元素上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。它按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据时从栈顶开始弹出数据（最后一个数据被第一个读出来）。栈具有记忆作用，对栈的插入与删除操作中，不需要改变栈底指针。（C语言版栈在这里--->https://blog.youkuaiyun.com/qq_38193883/article/details/97660986）

关于队列 的理解： 先进先出(First In First Out) 又称作FIFO表         也是一种运算受限的线性表，它的运算限制与栈不同，是两头都有限制，插入只能在表的一端进行(只进不出)，而删除只能在表的另一端进行(只出不进)，允许删除的一端称为队尾(rear)，允许插入的一端称为队头 (front) (C语言版队列在这里--->https://blog.youkuaiyun.com/qq_38193883/article/details/97661165)

图示：

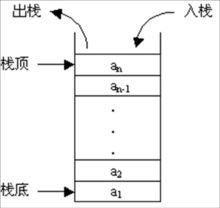
栈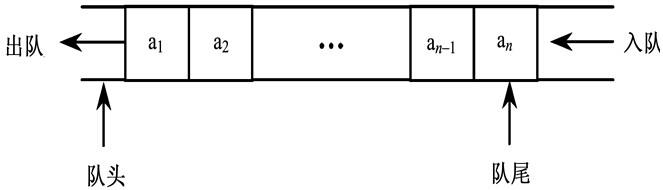

队列

栈基本操作：
头文件：
#include<algorithm> //是”STL 通用算法“的头文件
#include<queue>// 队列 
#include<stack>//栈
定义方式：
stack<datatype>  s;//栈的定义方式 参数是数据类型可根据具体需求修改为int double float等  
queue<datatype>  q; //队列的定义方式  参数是数据类型可根据具体需求修改为int double float等
基本操作：
                 //栈：
   s.empty()    //如果栈为空返回true，否则返回false  
   s.size()    //返回栈中元素的个数  
   s.pop()    //删除栈顶元素但不返回其值  
   s.top()   //返回栈顶的元素，但不删除该元素  
   s.push(e)//在栈顶压入新元素 ，参数e为要压入的元素
//队列：
q.empty()  // 如果队列为空返回true，否则返回false  
q.size()   // 返回队列中元素的个数  
q.pop()    //删除队列首元素但不返回其值  
q.front()  // 返回队首元素的值，但不删除该元素  
q.push(X)  //在队尾压入新元素 ，X为要压入的元素
q.back()   //返回队列尾元素的值，但不删除该元素  
应用举例：
Example one:

HDU Problem 简单计算器【栈】

Problem Description
读入一个只包含 +, -, *, / 的非负整数计算表达式，计算该表达式的值。

Input
测试输入包含若干测试用例，每个测试用例占一行，每行不超过200个字符，整数和运算符之间用一个空格分隔。没有非法表达式。当一行中只有0时输入结束，相应的结果不要输出。

Output
对每个测试用例输出1行，即该表达式的值，精确到小数点后2位。

Sample Input
1 + 2 4 + 2 * 5 - 7 / 11 0

Sample Output
3.00 13.36
#include <algorithm>
#include <cstdio>
#include <queue>
#include <stack>

#define MAX_N 1000
using namespace std;


int main(){
    double n, temp;
    char a, s[2];
    while (scanf("%lf%c", &n, &a)) {  
        if (n == 0 && a == '\n') break;      //当一行中只有0时输入结束，相应的结果不要输出 
        double sum = 0;                     //用于记录栈中元素之和 
        stack<double> stk;
        stk.push(n);                       //先把第一个输入的数值压栈 
        while (scanf("%s %lf", s, &n) != EOF) {
            if (s[0] == '+')   stk.push(n);
            else if (s[0] == '-')  stk.push(-n);         //是jian号就相当于加负数 
            else if (s[0] == '*') {
                temp = n*stk.top();
                stk.pop();         //乘法：先把栈顶元素（乘法前面的数）与n相乘再讲栈顶替换为积 
                stk.push(temp);
            }
            else {
                temp = stk.top()/n;
                stk.pop();        //除法：同乘法思路 
                stk.push(temp);
            }
		  a = getchar() ;   //当一行输入结束时 
	      if ( a == '\n'){
				break; }          //跳出循环计算结果 
        }
        while (!stk.empty()) {
            sum += stk.top();
            stk.pop();           //逐个出栈，累加 
        }
        printf("%.2lf\n", sum);
    }
    return 0;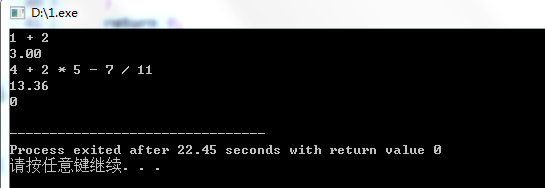
}
运行结果

Example two :

栈：表达式求值（中缀表达式转换为后缀表达式） --->点击查看（表达式求值）
   Example three  :

   队列：约瑟夫（Josephus）--->点我查看

正经致谢：