1.问题描述
图像表示的难点在于它的高维度。二维的p×q的灰度图像就有一个维度为1×pq的特征,所以一张100×100的图像就有一个10000维的特征。这个数据对于任何计算来说都是庞大的,但是否所有维度的信息都是有用的?其实,我们只要找到存储着大量信息的部分就行。Principal Components Analysis (PCA) 由karl
等人提出,它将一组可能相关的变量变成较小的一组不相关的变量。它的思想是一个高维的数据通常由相关变量描述,因此仅有少部分维度具有大量有意义信息。PCA方法查找数据中方差最大的方向,也就是主成分。
2.计算公式
给定随机的向量 X = x 1 , x 2 , . . , x n X={x_1,x_2,..,x_n} X=x1,x2,..,xn,其中 x i ∈ R d x_i \in \R^d xi∈Rd。
- 计算均值

- 计算协方差矩阵S
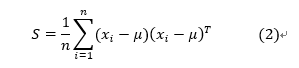
- 计算S的特征值和特征向量

- 根据特征值对特征向量降序排序,选择前k个。向量x的k个主成分为:
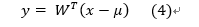
其中, W = ( v 1 , v 2 , . . , v k ) W=(v_1,v_2,..,v_k) W=(v1,v2,..,vk),利用PCA进行的重构为:

最后,利用eigenface进行人脸识别的过程如下:
a. 利用式(4),将所有的训练样本投影到PCA子空间。
b. 利用式(5),将所有的测试样本投到PCA子空间。
c. 在投影后的测试样本和








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








