学堂在线数据结构作业下1

二叉搜索树
a.概述
1.二叉搜索树之区别于普通的二叉树在于：任意节点均不大于其右子树中的节点，不小于其左子树中的节点
2.二叉搜索树的何种遍历序列是递增的？中序

b1.查找
1.在含n个节点的BST中进行查找的最坏时间复杂度为O(n)
2.在以上二叉查找树中查找关键码13，经过的节点依次为：

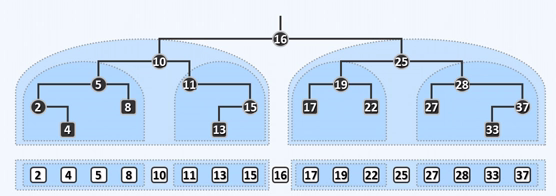
16, 10, 11, 15, 13

b2.插入
1.对BST进行插入操作，对待插入的目标元素e进行查找后，若查找失败，_hot指向的节点为：e被插入后的父亲

b3.删除
1.当欲删除的节点v在BST中的度为2时，实际被删除的节点为：
v的右子树中左侧分支的最后一个节点
解析：即v在中序遍历下的直接后继

c.平衡与等价
1.在含n个节点、高度为h的BST中进行查找的最坏时间复杂度为：
O(h)
2.含n个节点，高度为h的BST称为平衡二叉搜索树若它满足：h=O(log2n)
3.两个等价的平衡二叉搜索树有相同的：中序遍历序列

d1.
1.在AVL树中刚插入一个节点后失衡节点个数最多为O(lgn)
2.在AVL树中刚删除一个节点后失衡节点个数最多为O(1)
3.以下AVL树根节点的平衡因子为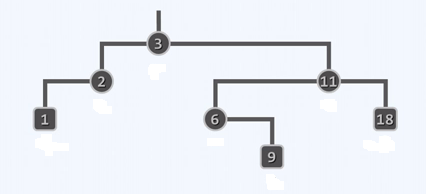
-1
解析：平衡因子=左子树高度-右子树高度
4.高度为3的AVL树至少包含几个节点？7

d2.插入
AVL树中插入节点引发失衡，经旋转调整后重新平衡，此时包含节点g,p,v的子树高度
不变
解析：在AVL树中修正插入节点引发的失衡不会出现失衡传播

d3.删除
AVL树中