全排列
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
例如:
1 、2 、3三个元素的全排列为:
{1,2,3},{1,3,2},{2,1,3},{2,3,1},{3,1,2},{3,2,1}。
设R={r1,r2,…,rn}是要进行排列的n个元素,Ri=R-{ri}。
集合X中元素的全排列记为perm(X)。
(ri)perm(X)表示在全排列perm(X)的每一个排列前加上前缀得到的排列。
R的全排列可归纳定义如下:
当n=1时,perm(R)=(r),其中r是集合R中唯一的元素;
当n>1时,perm(R)由(r1)perm(R1),(r2)perm(R2),…,(rn)perm(Rn)构成。
很明显全排列问题具有递归结构。
实现思想:将整组数中的所有的数分别与第一个数交换,这样就总是在处理后n-1个数的全排列。
实现
1、首先要写一个交换函数swap,实现将数组中两个元素交换位置
/**
* 交换函数,将数组中元素交换
* @param s
* @param i
* @param j
*/
public static void swap(int[] s,int i,int j) {
int temp = s[j];
s[j] = s[i];
s[i] = temp;
}
2、核心递归算法代码
/**
* 核心代码
* @param s
* @param start
* @param end
*/
public static void Perm(int[] s,int start,int end) {
if(start == end) {
for(int i = 0;i<=end; i++) {
System.out.print(s[i] + " ");
}
System.out.println();
}
for(int i = start;i<=end;i++) {
swap(s,start,i);
Perm(s,start+1,end);
swap(s,start,i);
}
}
3、在main函数中写int[] s = {1,2,3}; Perm(s,0,2);这两行代码,可以将1,2,3的全排列显示出来:
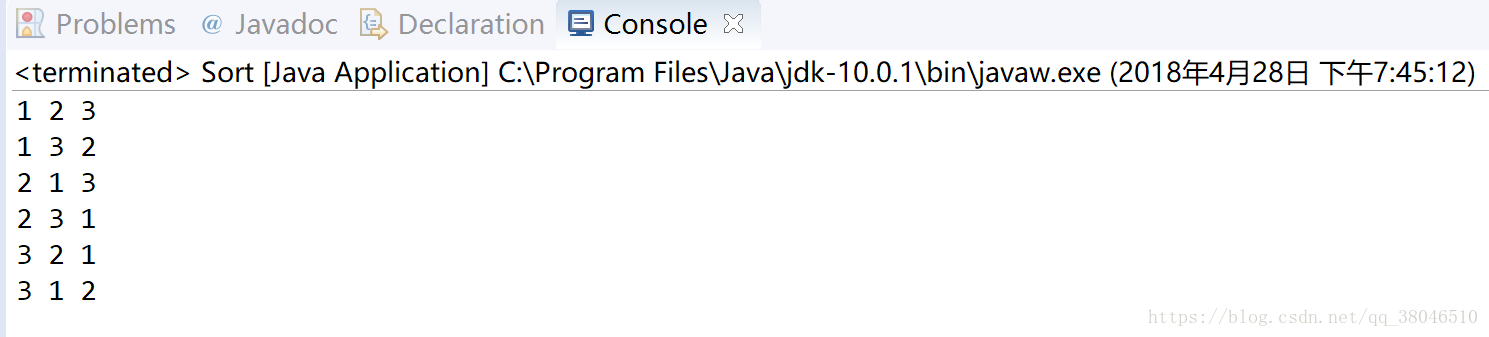
改进
这个方法存在一个问题,如果原数组中存在两个或以上的元素相等的话,输出会有重复结果,所以这里对函数添加一下判断条件:
/**
* 核心代码
* @param s
* @param start
* @param end
*/
public static void Perm(int[] s,int start,int end) {
if(start == end) {
for(int i = 0;i<=end; i++) {
System.out.print(s[i] + " ");
}
System.out.println();
}
for(int i = start;i<=end;i++) {
if(i == start || s[i] != s[start]) {
swap(s,start,i);
Perm(s,start+1,end);
swap(s,start,i);
}
}
}
输出:
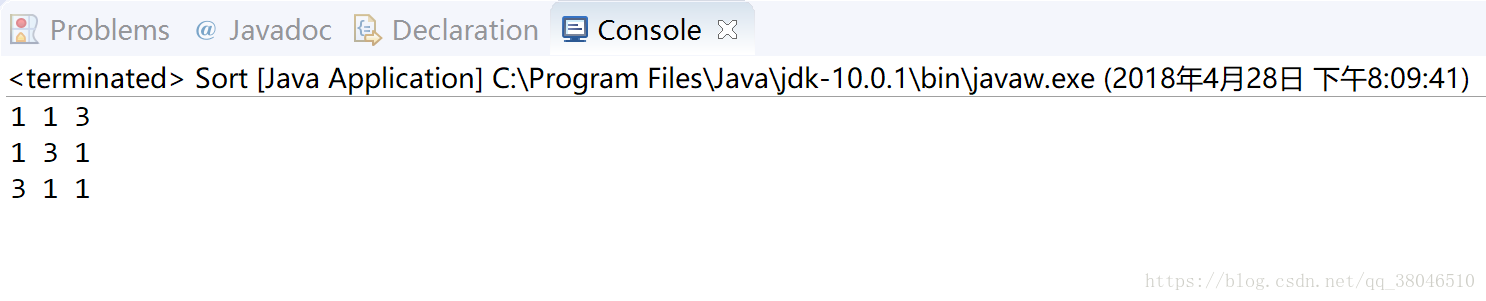


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








