C/C++ 《剑指offer》——（4）重建二叉树

问题描述：

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解题思路及知识点

在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。设L、D、R分别表示遍历左子树、访问根结点和遍历右子树， 则对一棵二叉树的遍历有三种情况：DLR（称为先序遍历），LDR（称为中序遍历），LRD （称为后序遍历）。

 结合题意确定思路

• 先序遍历：首先访问根，再先序遍历左子树，最后先序遍历右子树；
• 中序遍历：首先中序遍历左子树，再访问根，最后中序遍历右子树；
• 后序遍历：首先后序遍历左子树，再后序遍历右子树，最后访问根。

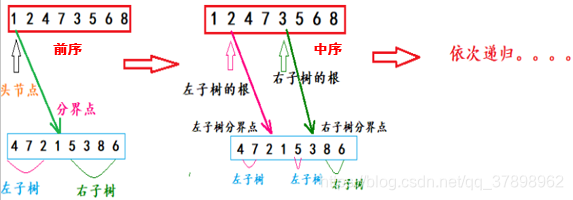
1. 前序遍历的第一个节点为二叉树的头节点

2. 根据头节点在中序遍历中找出头节点，并以此为分界点划分左子树和右子树

3. 由于前序遍历都是先遍历子树的头节点，故此在前序中找左子树的头节点，和右子树的头节点

4. 根据头节点在中序遍历中找寻分界点，划分左子树和右子树，依次类推

   

 牛客网在线编程剑指offer测试通过

#include<iostream>
#include<cstdlib>
#include<stack>
#include<vector>
using namespace std;
struct TreeNode{
int val;
TreeNode *l;
TreeNode *r;
TreeNode(int x) : val(x), l(NULL), r(NULL) {}
};
class Solution {
public:
	TreeNode* reConstructBinaryTree(vector<int> xx, vector<int> zx) {
		int data_size = xx.size();
		if (data_size == 0)
		{
			return NULL;
		}
		vector<int> xx_l, xx_r, zx_l, zx_r;//准备递归参数
		int head_value = xx.front();
		TreeNode* root = new TreeNode(head_value);
		int i = 0; //i中序遍历分界点
		for (; i < zx.size(); i++)
		{
			if (head_value == zx[i])
			{
				break;
			}
		}
		for (int j = 1; j < xx.size(); j++)
		{
			if (j <= i)
			{
				xx_l.push_back(xx[j]);
			}
			else
			{
				xx_r.push_back(xx[j]);

			}
		}

		for (int j = 0; j < zx.size(); j++)
		{
			if (j < i)
			{
				zx_l.push_back(zx[j]);
			}
			else if (j > i)
			{
				zx_r.push_back(zx[j]);

			}
		}

		root->l = reConstructBinaryTree(xx_l, zx_l);
		root->r = reConstructBinaryTree(xx_r, zx_r);
		cout << root->val;
		return root;
	}
};
int main()
{
	Solution *s = new Solution();
	vector<int> v1 = { 1,2,4,7,3,5,6,8 };
	vector<int> v2 = { 4,7,2,1,5,3,8,6 };
	s->reConstructBinaryTree(v1, v2);
	return 0;
}

 

 

 

 

 

 

请多多指教！如发现有错误，请及时告知。谢谢！

有疑问可评论或者私信，在能力范围内有问必答！