引言
今天分享的内容有:首先聊聊深度学习中存在的过拟合、欠拟合现象,以及梯度消失、梯度爆炸等。其次,分享一个本人梳理的卷积神经网络、循环神经网络代码结构。
过拟合、欠拟合
模型的泛化能力是深度学习的一大问题,所谓泛化能力就是模型在训练数据集和测试数据集上的表现情况。泛化能力强的模型,在训练数据集和测试数据集上都具有良好的表现;泛化能力差的模型,往往在训练集上表现良好(或在训练数据集上表现也很差),同时,在测试数据集上的表现也同样差强人意。若泛化能力的模型主要分为两类:(1)如果在训练集表现差,在测试集表现同样很差,这可能是欠拟合导致;(2)如果模型在训练集表现非常好,在测试集上表现很差,则这便是过拟合导致的。如下图:

解决方案
欠拟合
- 增加训练数据集,加大训练次数,增加神经元等;
- 抽取更多特征加入模型训练,可以考虑将多个特征进行组合;
- 尝试更加复杂的模型,更换优化器、损失函数等;
- 采用数据增强等策略。
过拟合
- 增加验证集,如使用交叉验证法,为模型提供一个泛化能力的“参考”;
- 使用正则化方法,如L1、L2正则化;
- 对输入数据进行归一化处理;
- 使用dropout方法;
- 调整模型参数,如减小学习率等;
- 早停策略,选择合适的训练次数,避免训练的网络过度拟合训练数据。
梯度消失(爆炸)
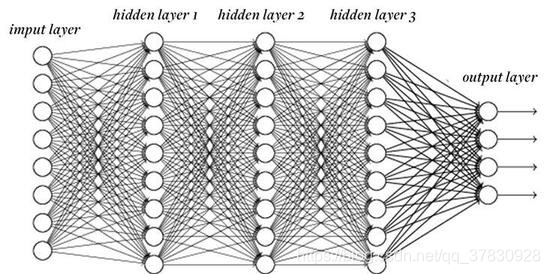

如上图,假设一个具有 L L L个隐藏层的全连接神经网络,,其第 l l l层 H l H^{l} Hl的权重参数为 W l W^{l} Wl,输出层 H L H^{L} HL的权重参数为 W L W^{L} WL,不考虑偏置值时,给定输入 X X X,第 l l l层的输出可表示为 H L = δ l ( ( δ 2 ( δ 1 ( X W 1 ) W 2 ) . . . ) W l ) H^{L} = \delta_{l}((\delta_{2}(\delta_{1} (XW^{1})W^{2})...)W^{l}) HL=δl((δ2(δ1(XW1)W2)...)Wl),此时,如果 L L L较大,则可能会出现梯度消失或梯度爆炸的情况。举个例子,假设 δ ( x ) = x \delta(x) = x δ(x)=x, W l = 0.2 ( 或 5 ) W^{l} = 0.2(或5) Wl=0.2(或5),当 L = 30 L = 30 L=30时,输出为 0. 2 30 ( 或 5 30 ) 0.2^{30}(或5^{30}) 0.230(或530),这就是梯度消失(爆炸)。
卷积神经网络
卷积神经网络的输入是一个二维输入数组和一个二维核(kernel)数组,输出也是一个二维数组,其中核数组通常称为卷积核或过滤器(filter)。卷积核的尺寸通常小于输入数组,卷积核在输入数组上滑动,在每个位置上,卷积核与该位置处的输入子数组按元素相乘并求和,得到输出数组中相应位置的元素。下图展示了一个互相关运算的例子。
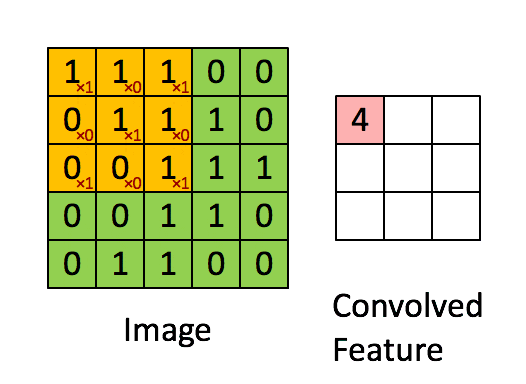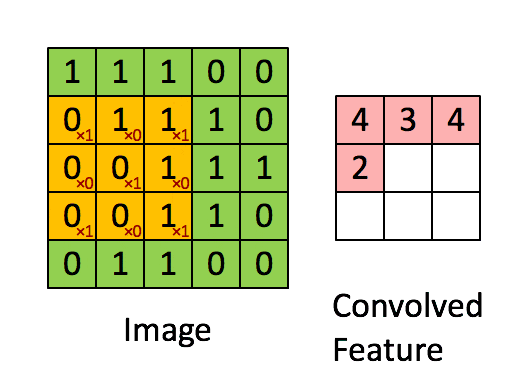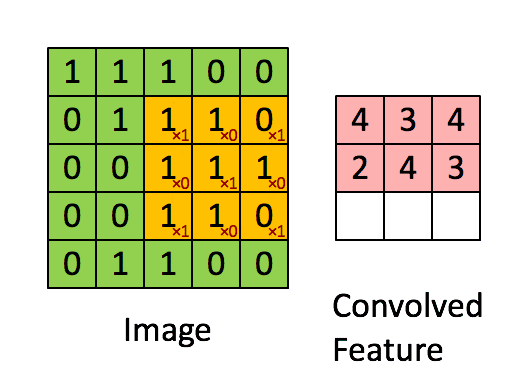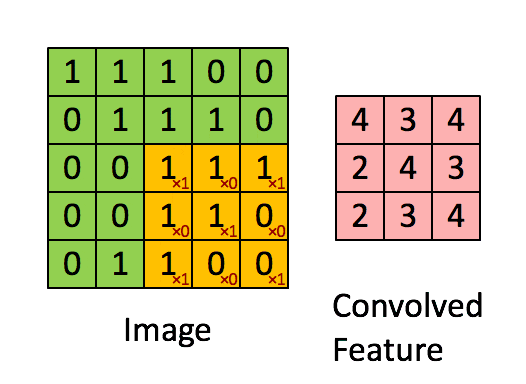
在卷积神经网络中,主要有以下几个概念:
(1) 特征图:二维卷积层输出的二维数组可以看作是输入在空间维度(宽和高)上某一级的表征,也叫特征图。
(2) 感受野:影响元素 x 的前向计算的所有可能输入区域(可能大于输入的实际尺寸)叫做 x 的感受野(receptive field)。
(3) 卷积核:如上图黄色标记部分即为卷积核。一个卷积核对应着一个特征图。
(4) 填充:填充(padding)是指在输入高和宽的两侧填充元素(通常是0元素)。
(5) 步幅: 卷积核在输入数组上滑动,每次滑动的行数与列数即是步幅(stride)。
(6) 通道:色图像在高和宽2个维度外还有RGB(红、绿、蓝)3个颜色通道。假设彩色图像的高和宽分别是 h 和 w (像素),那么它可以表示为一个 3×h×w 的多维数组,我们将大小为3的这一维称为通道(channel)维。
(7) 池化:池化层主要用于缓解卷积层对位置的过度敏感性,往往配合着卷积层使用。同卷积层一样,池化层每次对输入数据的一个固定形状窗口(又称池化窗口)中的元素计算输出,池化层直接计算池化窗口内元素的最大值或者平均值,该运算也分别叫做最大池化或平均池化。不同的是,在处理多通道输入数据时,池化层对每个输入通道分别池化,但不会像卷积层那样将各通道的结果按通道相加。这意味着池化层的输出通道数与输入通道数相等。
计算公式:
在构建卷积神经网络时,最重要的莫过于计算卷积操作后的张量形状。
公
式
:
(
n
h
+
p
h
−
k
h
+
1
)
×
(
n
w
+
p
w
−
k
w
+
1
)
公式:(n_{h} + p_{h} - k_{h} + 1) \times (n_{w} + p_{w} - k_{w} + 1)
公式:(nh+ph−kh+1)×(nw+pw−kw+1)
其中,
n
h
n_{h}
nh代表输入图像的高度
p
h
p_{h}
ph代表填充值
k
h
k_{h}
kh代表卷积核的高度,
w
w
w代表宽度。
下面是一个例子(LeNet)的实现。其结构图如下所示:

#import
import sys
import torch
import torch.nn as nn
import torch.optim as optim
import time
#net
class Flatten(torch.nn.Module): #展平操作
def forward(self, x):
return x.view(x.shape[0], -1)
class Reshape(torch.nn.Module): #将图像大小重定型
def forward(self, x):
return x.view(-1,1,28,28) #(B x C x H x W)
# 定义模型
net = torch.nn.Sequential( #Lelet
Reshape(),
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2), #b*1*28*28 =>b*6*28*28
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), #b*6*28*28 =>b*6*14*14
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5), #b*6*14*14 =>b*16*10*10
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), #b*16*10*10 => b*16*5*5
Flatten(), #b*16*5*5 => b*400
nn.Linear(in_features=16*5*5, out_features=120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
# 获取数据
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
def try_gpu():
# 如果有GPU资源可以使用GPU
if torch.cuda.is_available():
device = torch.device('cuda:0')
else:
device = torch.device('cpu')
return device
device = try_gpu()
def evaluate_accuracy(data_iter, net,device=torch.device('cpu')):
"""验证模型的准确率"""
acc_sum,n = torch.tensor([0],dtype=torch.float32,device=device),0
for X,y in data_iter:
# If device is the GPU, copy the data to the GPU.
X,y = X.to(device),y.to(device)
net.eval()
with torch.no_grad():
y = y.long()
acc_sum += torch.sum((torch.argmax(net(X), dim=1) == y)) #[[0.2 ,0.4 ,0.5 ,0.6 ,0.8] ,[ 0.1,0.2 ,0.4 ,0.3 ,0.1]] => [ 4 , 2 ]
n += y.shape[0]
return acc_sum.item()/n
def train_ch5(net, train_iter, test_iter,criterion, num_epochs, batch_size, device,lr=None):
"""定义模型训练"""
print('training on', device)
net.to(device)
optimizer = optim.SGD(net.parameters(), lr=lr)
for epoch in range(num_epochs):
train_l_sum = torch.tensor([0.0],dtype=torch.float32,device=device)
train_acc_sum = torch.tensor([0.0],dtype=torch.float32,device=device)
n, start = 0, time.time()
for X, y in train_iter:
net.train()
optimizer.zero_grad()
X,y = X.to(device),y.to(device)
y_hat = net(X)
loss = criterion(y_hat, y)
loss.backward()
optimizer.step()
with torch.no_grad():
y = y.long()
train_l_sum += loss.float()
train_acc_sum += (torch.sum((torch.argmax(y_hat, dim=1) == y))).float()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net,device)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, '
'time %.1f sec'
% (epoch + 1, train_l_sum/n, train_acc_sum/n, test_acc,
time.time() - start))
# 设置一些训练参数
lr, num_epochs = 0.9, 10
batch_size = 256
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
torch.nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
net = net.to(device)
# 定义损失函数
criterion = nn.CrossEntropyLoss()
train_ch5(net, train_iter, test_iter, criterion,num_epochs, batch_size,device, lr)
# 开始测试
for testdata,testlabe in test_iter:
testdata,testlabe = testdata.to(device),testlabe.to(device)
break
print(testdata.shape,testlabe.shape)
net.eval()
y_pre = net(testdata)
print(torch.argmax(y_pre,dim=1))
print(testlabe)
循环神经网络
循环神经网络(Recurrent neural network, RNN):也叫递归神经网络,不同于卷积神经网络,RNN更擅长对序列数据进行建模处理。全连接神经网络和卷积神经网络都默认前一个输入和后一个输入是完全没有关系的。但是,某些任务需要能够更好的处理序列的信息,即前面的输入和后面的输入是有关系的。比如,在做句子预测的时候,我是中国人,我会说____ 。如果我们的模型能够更好的捕捉到“中国人”这一信息,对于句子的预测将会提供极大的帮助。

如上图所示,等号右边是RNN模型的展开形式,循环神经网络引入一个隐藏变量
H
H
H,用
h
t
h_{t}
ht表示
H
H
H在时间步
t
t
t的值。
h
t
h_{t}
ht的计算基于
X
t
X_{t}
Xt和
h
t
−
1
h_{t - 1}
ht−1,可以认为
H
t
H_{t}
Ht记录了当前时刻之前的序列信息。其计算公式如下:
h
t
=
δ
(
X
t
W
x
h
+
h
t
−
1
W
h
h
+
b
h
)
h_{t} = \delta(X_{t} W_{xh} + h_{t-1}W_{hh} + b_{h})
ht=δ(XtWxh+ht−1Whh+bh)
O
t
=
h
t
W
h
q
+
b
q
O_{t} = h_{t}W_{hq} + b_{q}
Ot=htWhq+bq 其中,
W
x
h
∈
R
d
×
h
W_{xh}\in\mathbb{R^{d\times h}}
Wxh∈Rd×h,
W
h
h
∈
R
h
×
h
W_{hh}\in\mathbb{R^{h\times h}}
Whh∈Rh×h,
b
h
∈
R
1
×
h
b_{h}\in\mathbb{R^{1\times h}}
bh∈R1×h,
δ
\delta
δ是非线性激活函数。更多信息可以参考RNN。目前,使用更多的是RNN的变体:LSTM和GRU。
下面是LSTM的代码实现:
import os
import numpy as np
import torch
from torch import nn, optim
import torch.nn.functional as F
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def load_data_jay_lyrics():
"""加载周杰伦歌词数据集"""
with open('./jaychou_lyrics.txt','r',encoding = 'utf-8') as f:
corpus_chars = f.read()
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
idx_to_char = list(set(corpus_chars))
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
vocab_size = len(char_to_idx)
corpus_indices = [char_to_idx[char] for char in corpus_chars]
return corpus_indices, char_to_idx, idx_to_char, vocab_size
# 载入数据集
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()
# 设置一些超参数
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xi, W_hi, b_i = _three() # 输入门参数
W_xf, W_hf, b_f = _three() # 遗忘门参数
W_xo, W_ho, b_o = _three() # 输出门参数
W_xc, W_hc, b_c = _three() # 候选记忆细胞参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
C = F * C + I * C_tilda
H = O * C.tanh()
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H, C)
def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, is_random_iter, num_epochs, num_steps,
lr, clipping_theta, batch_size, pred_period,
pred_len, prefixes):
if is_random_iter:
data_iter_fn = data_iter_random
else:
data_iter_fn = data_iter_consecutive
params = get_params()
loss = nn.CrossEntropyLoss()
for epoch in range(num_epochs):
if not is_random_iter: # 如使用相邻采样,在epoch开始时初始化隐藏状态
state = init_rnn_state(batch_size, num_hiddens, device)
l_sum, n, start = 0.0, 0, time.time()
data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)
for X, Y in data_iter:
if is_random_iter: # 如使用随机采样,在每个小批量更新前初始化隐藏状态
state = init_rnn_state(batch_size, num_hiddens, device)
else:
# 否则需要使用detach函数从计算图分离隐藏状态, 这是为了
# 使模型参数的梯度计算只依赖一次迭代读取的小批量序列(防止梯度计算开销太大)
for s in state:
s.detach_()
inputs = to_onehot(X, vocab_size)
# outputs有num_steps个形状为(batch_size, vocab_size)的矩阵
(outputs, state) = rnn(inputs, state, params)
# 拼接之后形状为(num_steps * batch_size, vocab_size)
outputs = torch.cat(outputs, dim=0)
# Y的形状是(batch_size, num_steps),转置后再变成长度为
# batch * num_steps 的向量,这样跟输出的行一一对应
y = torch.transpose(Y, 0, 1).contiguous().view(-1)
# 使用交叉熵损失计算平均分类误差
l = loss(outputs, y.long())
# 梯度清0
if params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
grad_clipping(params, clipping_theta, device) # 裁剪梯度
sgd(params, lr, 1) # 因为误差已经取过均值,梯度不用再做平均
l_sum += l.item() * y.shape[0]
n += y.shape[0]
if (epoch + 1) % pred_period == 0:
print('epoch %d, perplexity %f, time %.2f sec' % (
epoch + 1, math.exp(l_sum / n), time.time() - start))
for prefix in prefixes:
print(' -', predict_rnn(prefix, pred_len, rnn, params, init_rnn_state,
num_hiddens, vocab_size, device, idx_to_char, char_to_idx))
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
train_and_predict_rnn(lstm, get_params, init_lstm_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)







 探讨深度学习中过拟合、欠拟合、梯度消失等问题,分享卷积神经网络(CNN)、循环神经网络(RNN)代码结构及解决策略。
探讨深度学习中过拟合、欠拟合、梯度消失等问题,分享卷积神经网络(CNN)、循环神经网络(RNN)代码结构及解决策略。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








