Leetcode 2135. Count Words Obtained After Adding a Letter_为什么sum(1 << ord(c)

本文链接：https://blog.youkuaiyun.com/qq_37821701/article/details/125675197

这篇博客介绍了LeetCode 2135题目的三种解法：将单词转换为字符串、使用位掩码以及Trie树。通过将目标单词减少一个字符，检查起始单词中是否存在同构字符串。文章详细分析了每种方法的时间复杂度，并指出位掩码操作更高效且避免了字符串转化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

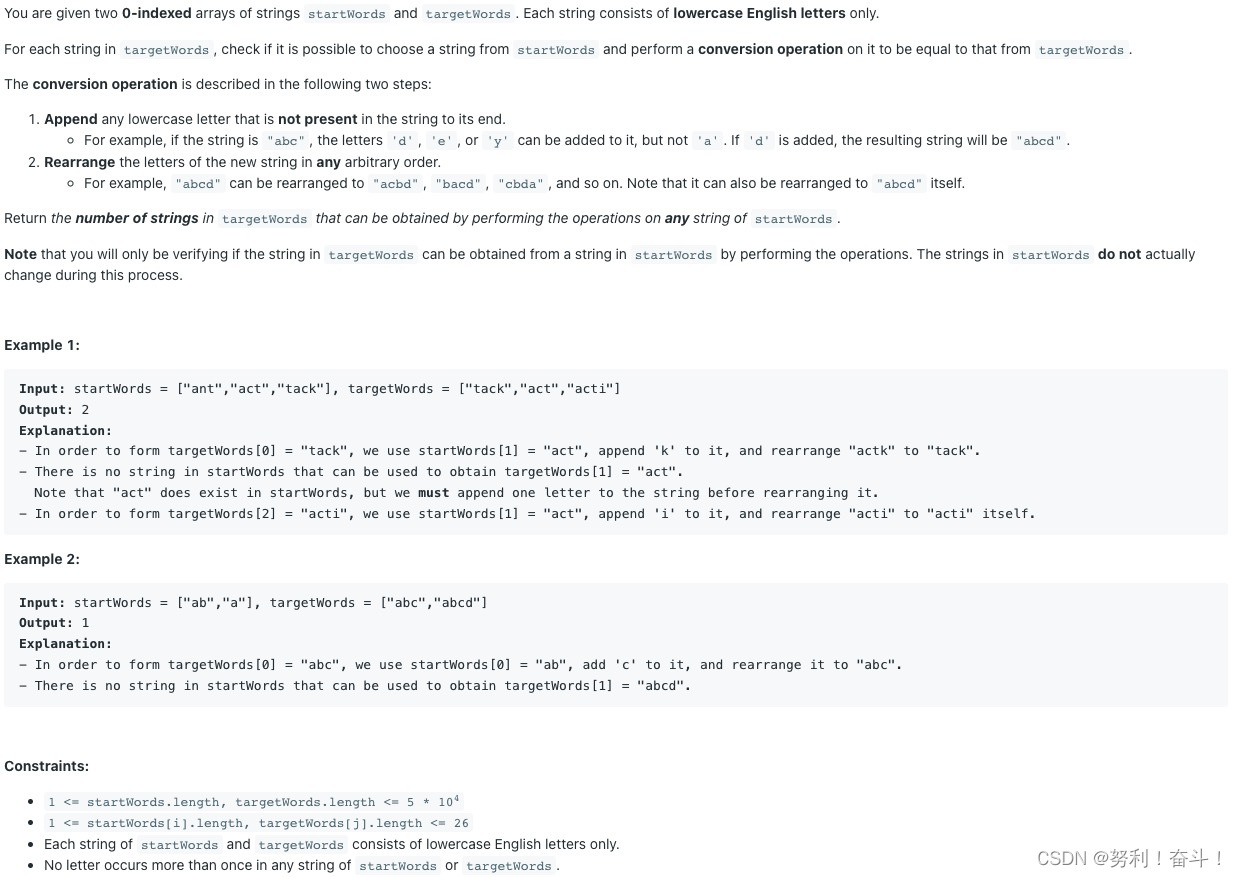
在这里插入图片描述

解法1:转化成字符串

对于每一个target word，减去任意一个字符之后，找start word里面有没有它的同构字符串
由于list不能作为hash key，所以可以用一个长度为26的01字符串来代替

class Solution:
    def wordCount(self, startWords: List[str], targetWords: List[str]) -> int:
        start_dict = {}
        for w in startWords:
            tmp = ['0'] * 26
            for c in w:
                tmp[ord(c) - ord('a')] = '1'
            tmp_str = ''.join(tmp)
            start_dict[tmp_str] = True
        
        ans = 0
        for w in targetWords:
            tmp = ['0'] * 26
            for c in w:
                tmp[ord(c)-ord('a')] = '1'
            for c in w:
                tmp[ord(c)-ord('a')] = '0'
                if ''.join(tmp) in start_dict:
                    ans += 1
                    break
                tmp[ord(c)-ord('a')] = '1'
                
        return ans

时间复杂度：O(nm2), n为target word个数，m为word的平均长度

解法2:bitmask

bitmask的思路是和上面相同的，只是这边把string转化为二进制数字，具体操作为
m = 0
for c in w:
m ^= 1 << ord© - ord(‘a’)
这个的意思是，首先对于字符c，用1左移几位得到一个只有那个位置为1，其他位置为0的二进制数，然后用当前的书去xor，那么这位就会变成1，由于每个字符只出现一次，这样的操作就可以把出现的字符的相应位置设为1，其他为0
m ｜= 1 << ord© - ord(‘a’)也是会有同样效果的

class Solution:
    def wordCount(self, startWords: List[str], targetWords: List[str]) -> int:
        start_dict = {}
        for w in startWords:
            m = 0
            for c in w:
                m ^= 1 << ord(c) - ord('a')
            start_dict[m] = True
        
        ans = 0
        for w in targetWords:
            m = 0
            for c in w:
                m ^= 1 << ord(c) - ord('a')
            for c in w:
                if m ^ 1 << ord(c) - ord('a') in start_dict:
                    ans += 1
                    break
        
        return ans