Leetcode permutaion and combination 总结

题目1：无重复元素，permutation I

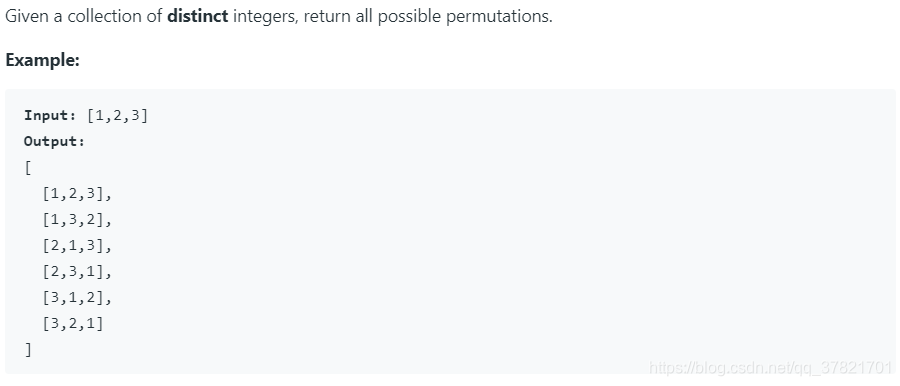
解析：

对于无重复的permutation可以当成一个模板记住
python代码如下：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def backtracking(curr,permutation):
            if curr==len(nums):
                ans.append(permutation[:])
                return
            
            for i in range(len(nums)):
                if not visited[i]:
                    permutation[curr] = nums[i]
                    visited[i] = True
                    backtracking(curr+1,permutation)
                    visited[i] = False
                    permutation[curr] = 0
        
        visited = [False]*len(nums)
        permutation = [0]*len(nums)
        ans = []
        backtracking(0,permutation)
        return ans

题目2：有重复元素，permutation II

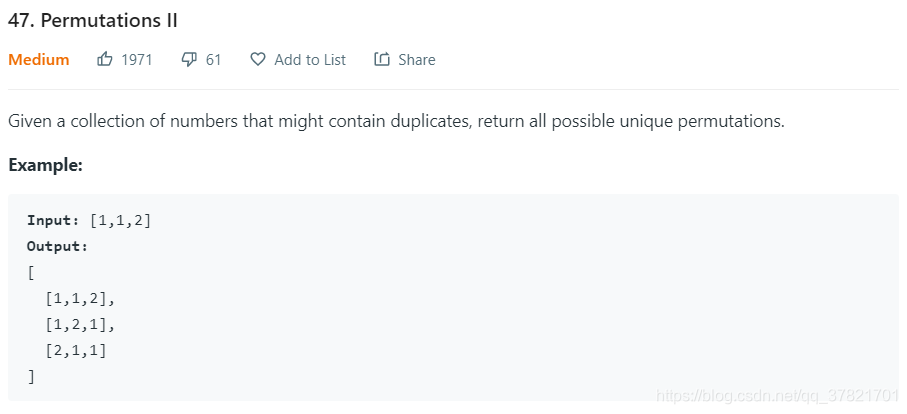
解析

有重复的permutation关键在于，对于产生的permutation，每个位置相同元素只能被放一次，之所以这么说因为这个相同元素可能来自于原数组的不同位置。所以我们需要两个visited的set：

• 一个全局的visited用来记录原数组的某个元素是否被用过了，这个确保原数组每个元素都被用且只被用一次
• 另一个local的visited用来记录我们当前在构造的permutation的某个位置是否被放过这个元素。相当于在backtracking进行DFS的时候，每个level有一个visited，这个visited只track当前level被放过的元素

python代码如下：
只需要在上面无重复的代码基础上加上几行就可以，对于原数组的排序加不加都是可以的，对于另一种需要排序但是会更快地方法见这里：
https://leetcode.com/submissions/detail/372121388/

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        def backtracking(curr,permutation):
            if curr==len(nums):
                ans.append(permutation[:])
                return
            visited_local = set()
            for i in range(len(nums)):
                #表示所给数组这个位置的数字还没被放过，但是由于有重复元素，即使这个位置的元素还没被放过，也有可能其他位置有重复元素已经被放过。所以这个全局的visited用来确保nums中的同一个位置的元素不会被重复的取
                if not visited[i]:
                    #所以上一步的检查还不够，需要进一步检查在permutation中现在的位置有没有放过这个元素。这个visited_local用来确保nums中不同位置的重复元素不会被放到permutation的同一个位置。可以对这两个情况分别举例子来说明
                    if nums[i] not in visited_local:
                        permutation[curr] = nums[i]
                        visited[i] = True
                        backtracking(curr+1,permutation)
                        visited[i] = False
                        permutation[curr] = 0
                        visited_local.add(nums[i])
                    else:
                        continue
        nums.sort()
        
        visited = [False]*len(nums)
        permutation = [0]*len(nums)
        ans = []
        backtracking(0,permutation)
        return ans

题目3：无重复元素，combination

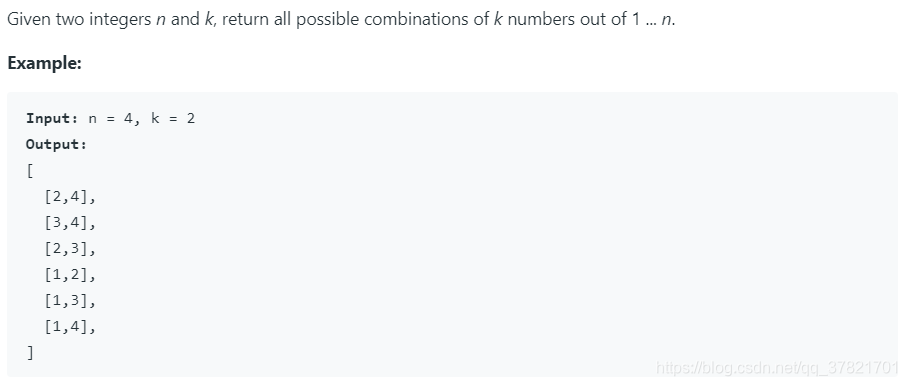
这也可以当作模板，跟permutation模板一起记。这边需要注意的是，在进入下一个level进行递归的时候，要传i+1而不是curr+1，否则是会出现重复的combination

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        def backtracking(curr,combination):
            if len(combination)==k:
                ans.append(combination[:])
                return
            for i in range(curr,n+1):
                combination.append(i)
                backtracking(i+1,combination)
                combination.pop()
            
        ans = []
        backtracking(1,[])
        return ans

题目4：combination sum，无重复元素，但每个元素可以用多次

无重复元素，所以无需排序。但每个位置可以用多次，所以传到下一层recursion的index无需加1

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        def backtracking(combination,level):
            if sum(combination)==target:
                ans.append(combination[:])
            
            if sum(combination)>target:
                return
            
            for i in range(level,len(nums)):
                combination.append(nums[i])
                backtracking(combination,i)
                combination.pop()
        
        ans = []
        nums = candidates
        backtracking([],0)
        return ans

题目4：combination sum II，有重复元素但是每个位置的元素只能用一次

• 每个位置元素只能用一次，所以传到下一层recursion的index需要加1
• 有重复元素，所以需要local_visited保证某个位置没有放过当前元素值
• 由于是combination，所以需要sort，不然就会产生有重复元素的permutation结果
• sort和visited是一定同时需要的，可以试着没有sort和visited会出现什么情况

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        def back_tracking(curr,combination):
            if sum(combination) == target:
                ans.append(combination[:])
                return
            if sum(combination) > target:
                return
            # visited用来确保combination的当前位置没有被放过这个元素，如果被放过这个元素，就可能出现重复的结果，因为这个元素可能与之前某个元素相同，但不在同一个位置
            visited = set()
            for i in range(curr,len(candidates)):
                if candidates[i] in visited:
                    continue
                combination.append(candidates[i])
                back_tracking(i+1,combination)
                combination.pop()
                visited.add(candidates[i])
            
        
        ans = []
        candidates.sort()
        back_tracking(0,[])
        return ans

对于上面四道题的解法，有一个共同需要注意的点，那就是在加入结果的时候必须是现在结果的值copy，因为我们在回溯的时候，只对一个对象数组进行了修改，在python中，这样传值会影响之前的结果，必须要append(permutation[:])或者append(combination[:])