数据结构和算法（10）：线索二叉树

首先我们看看下图中空指针有多少个呢？对于一个有n个节点的二叉链表，每个节点有指向左右孩子的两个指针域，所以一共是2n个指针域。而n个节点的二叉树一共有n-1条分支线数，也就是说，其实是存在2n-（n-1）=n+1个空指针域。比如下图有10个节点，而空指针域为11个。这些空间不存储任何事物，白白浪费着内存的资源。

另一个方面，我们在做遍历时，比如下图做中序遍历是，得到了HDIBJEAFCG这样的字符序列，遍历过后，我们可以知道，节点I的前驱是D，后继是B。也就是说，我们可以很清楚的知道任一个节点，他的前驱和后继是哪一个。可是这是建立在已经遍历过的基础上的。在二叉链表上，我们只能知道每个节点指向其左右孩子节点的地址，而不知道某个节点的前驱是谁，后继是谁。要想知道，必须再遍历一次。为什么不考虑在创建时就记住这些前驱和后继呢，那将是多大的时间上的节省。

这就是我们现在要研究的问题。我们把这种指向前驱和后继的指针成为线索，加上线索的二叉链表成为线索链表，响应的二叉树就称为线索二叉树。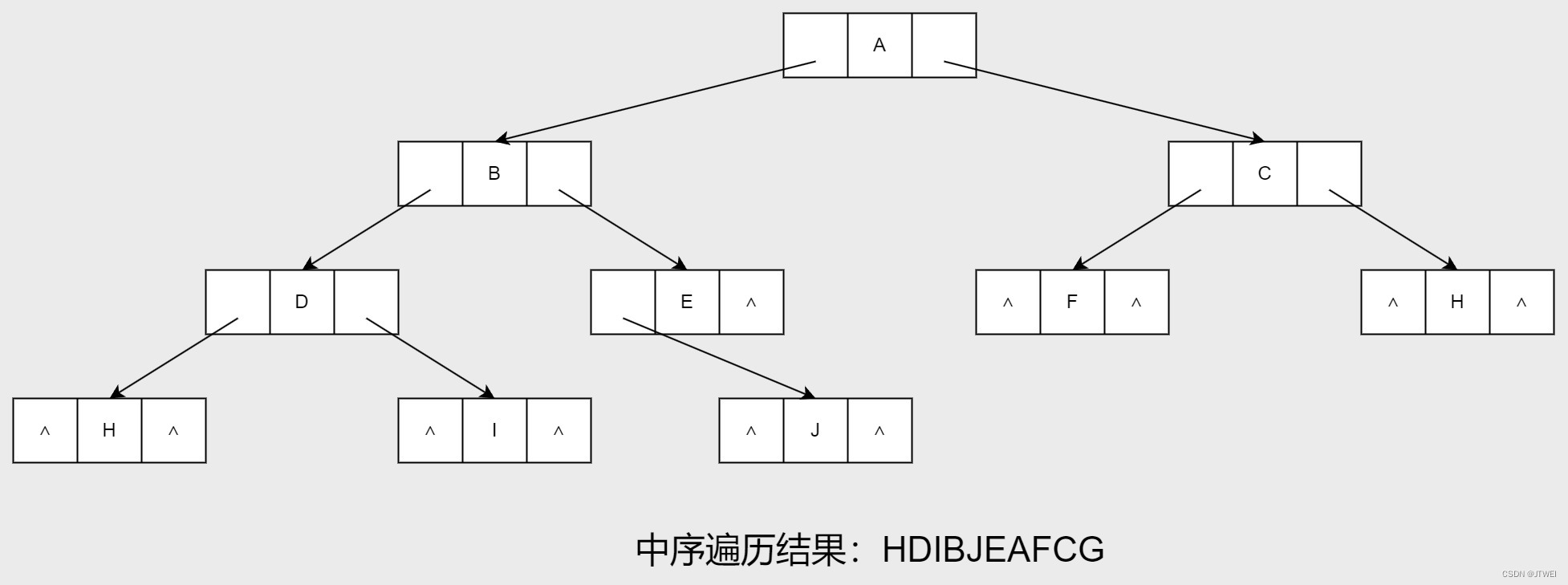

 我们现在找一下规律：

H的后继D，D的后继是I，I的后继是B，......,C的后继是G。假如，我们将所有的空指针域中的右孩子，改为指向他的后继节点，这样是否可以满足呢？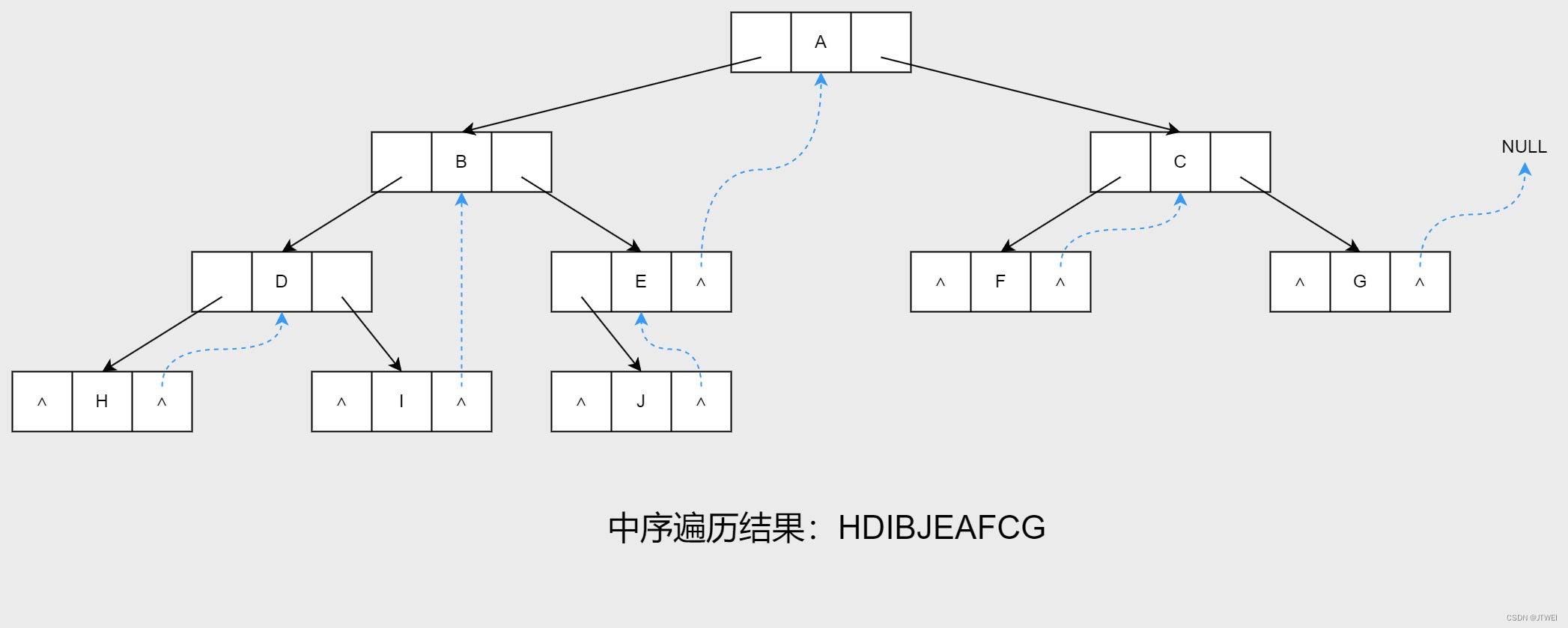

 我们将有后继的节点标为蓝色：HDIBJEAFCG，此时共有6个空指针域被利用。

我们将这棵二叉树的所有空指针域中的左孩子改为指向当前结点的前驱。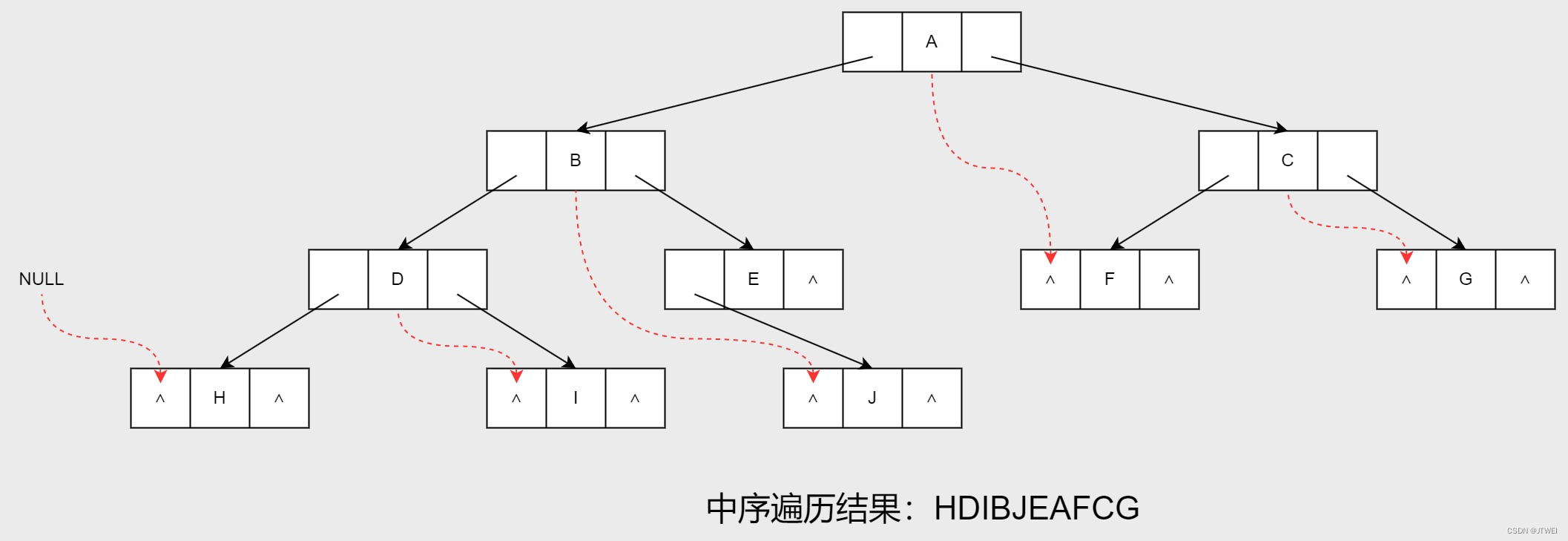

 我们将有前驱的节点标为红色：HDIBJEAFCG，此时共有5个空指针域被利用，证号和上面的后继加起来是11个。

现在我们把上面两个图合到一起。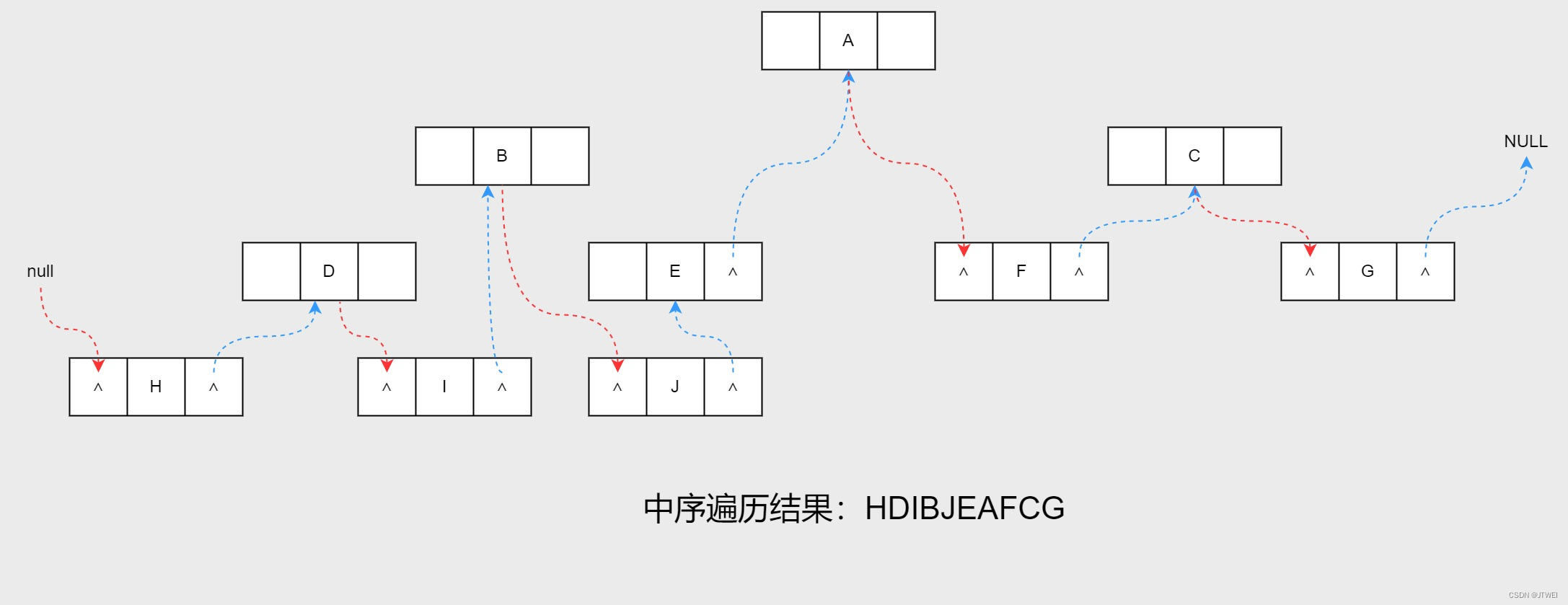

 从上图就更容易看出，其实线索二叉树，等于是把一棵二叉树转变成了一个双向链表，这样对我们的插入删除节点、查找某个节点都带来了方便。此时，我们对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化。

现在需要思考另一个问题，我们如何知道某一个节点的左节点是指向它的左孩子还是指向前驱？右节点是指向右孩子还是指向后继呢？因此，我们需要每个节点再增设两个标志域 Itag 和 rtag，注意Itag 和 rtag只是存放true 或false布尔类型变量，其占用的内存空间要小于像左孩子和右孩子的指针变量。

其中，tag为true时，指向该节点的左孩子。tag为false时，指向该节点的前驱或后继。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace ThreadedBinaryTree
{
    class ThreadNode
    {
        public int value;
        public bool lThread;
        public bool rThread;
        public ThreadNode? left_node;
        public ThreadNode? right_node;
        public ThreadNode(int value)
        {
            this.value = value;
            lThread = true;
            rThread = true;
            left_node = null;
            right_node = null;
        }
    }

    internal class ThreadedBinaryTree
    {
        //线索二叉树的根节点
        public ThreadNode? rootNode;

        //无传入参数的构造函数
        public ThreadedBinaryTree()
        {
            this.rootNode = null;
        }

        public ThreadedBinaryTree(int[] data)
        {
            for (int i = 0; i < data.Length; i++)
            {
                Add(data[i]);
            }
        }


        private void Add(int value)
        {

            ThreadNode? newNode = new ThreadNode(value);
            ThreadNode? current;
            ThreadNode? parent;
            ThreadNode? previous = new ThreadNode(value);
            int pos;

            //设置线索二叉树的开头节点
            if (rootNode == null)
            {
                rootNode = newNode;
                rootNode.left_node = rootNode;
                rootNode.right_node = null;
                rootNode.lThread = true;
                rootNode.rThread = false;
                return;
            }

            //设置开头节点所指的节点
            current = rootNode.right_node;
            if (current == null)
            {
                rootNode.right_node = newNode;
                newNode.left_node = rootNode;
                newNode.right_node = rootNode;
                return;
            }

            //父节点是开头节点
            parent = rootNode;
            //设置二叉树中的前进方向
            pos = 0;  
            while (current != null)
            {
                if (current.value > value)
                {
                    if (pos != -1)
                    {
                        pos = -1;
                        previous = parent;
                    }

                    parent = current;
                    // 如果是指针
                    if (current.lThread == false)
                        current = current.left_node;
                    else
                        current = null;
                }
                else
                {
                    if (pos != 1)
                    {
                        pos = 1;
                        previous = parent;
                    }
                    parent = current;
                    // 如果是指针
                    if (current.rThread ==false)
                        current = current.right_node;
                    else
                        current = null;
                }
            }

            if (parent.value > value)
            {
                parent.lThread = false;
                parent.left_node = newNode;
                newNode.left_node = previous;
                newNode.right_node = parent;
            }
            else
            {
                parent.rThread = false;
                parent.right_node = newNode;
                newNode.left_node = parent;
                newNode.right_node = previous;
            }
        }

        public void Print()
        {
            ThreadNode? tempNode;
            tempNode = rootNode;
            do
            {
                //如果是线索
                if (tempNode!.rThread == true)
                {
                    tempNode = tempNode.right_node;
                }
                else
                {
                    tempNode = tempNode.right_node;
                    //如果是指针
                    while (tempNode!.lThread == false)
                        tempNode = tempNode.left_node;
                }
                if (tempNode != rootNode)
                    Console.WriteLine(tempNode!.value);
            } while (tempNode != rootNode);
        }
    }
}

测试代码

//测试代码：
 internal static void TestFunc()
 {
     int[] intArr = { 0, 10, 20, 30, 100, 399, 453, 43, 237, 373, 655 };

     ThreadedBinaryTree tree = new ThreadedBinaryTree(intArr);
     tree.Print();
 }