目录
基本概念
树(Tree)是 n(n≥0)个结点的有限集。n=0时称为空树。在任意一棵非空树中:(1)有且仅有一个特定的称为根(Root)的结点;(2)n>1时,其余结点可分为m(m>0)个互不相交的有限集,其中每一个集合本身又是一棵树,并且称为跟的子树(SubTree).
对于树的定义还需要强调两点:1.n>0时根节点是唯一的,不可能存在多个跟节点。2.m>0时,子树的个数没有限制,但他们一定是互不相交的。(如果相交就成了图)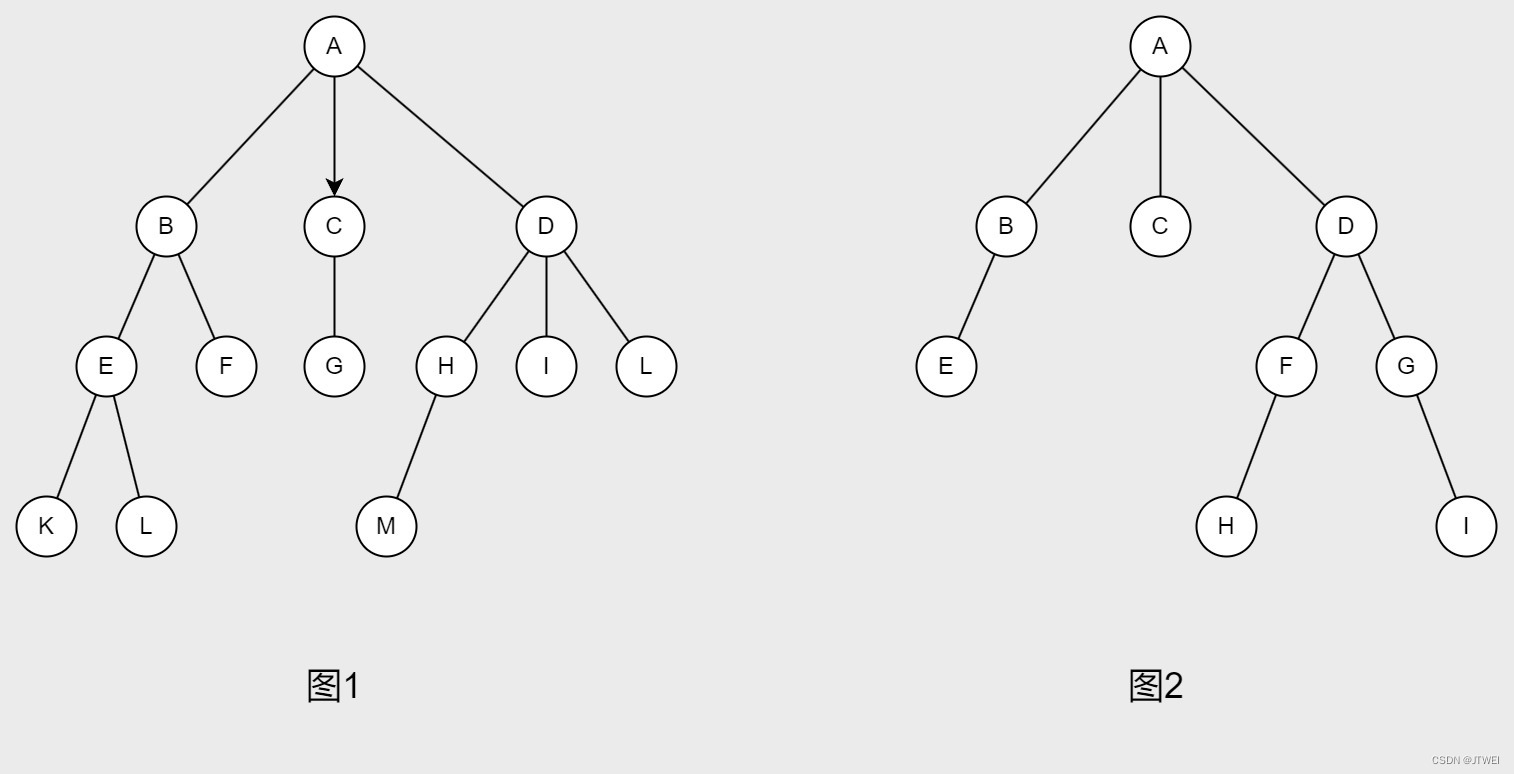
在树的结构中,有许多常用的专有名词。
-
度数(Degree):每个节点所有子树的个数。例如图1中节点B的度数为2,D的度数为3,F、K、I、J的度数为0.
-
层数(Level):树的层数,假设树根A为第一层,那么B、C、D节点的层数为2,E、F、G、H、I、J的层数为3。
-
高度(Height):树的最大层数
-
树叶或称为终端节点(Terminal Node):度数为0的结点就是树叶,如图1中K、L、F、G、M、I、J就是树叶。
-
父节点(Parent):每一个节点有连接的上一层节点即为父节点,如图1,F的父节点为B,而B的父节点为A。
-
子节点(Children):每一个节点有连接的下一层节点为子节点。如图1,A的子节点为B、C、D。
-
祖先(Ancestor):从树根到该节点路径上所包含的节点。如图1,K的祖先为A、B、E节点。
-
子孙(Descendent):在该节点往下追溯子树中的任一节点。如图1,B的子孙为E、F、K、L节点。
-
兄弟节点(Sibling):有共同父节点的节点为兄弟节点。如图1,B、C、D为兄弟节点。
-
非终端节点(Nonterminal Node):树叶以外的节点。如图1,A、B、C、D、E、H等。
-
同代(Generation):在同一棵树中具有相同层数的节点。如图1,B、C、D为同代节点。
-
有序树和无序树:如果将树中节点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
树的存储结构
双亲表示法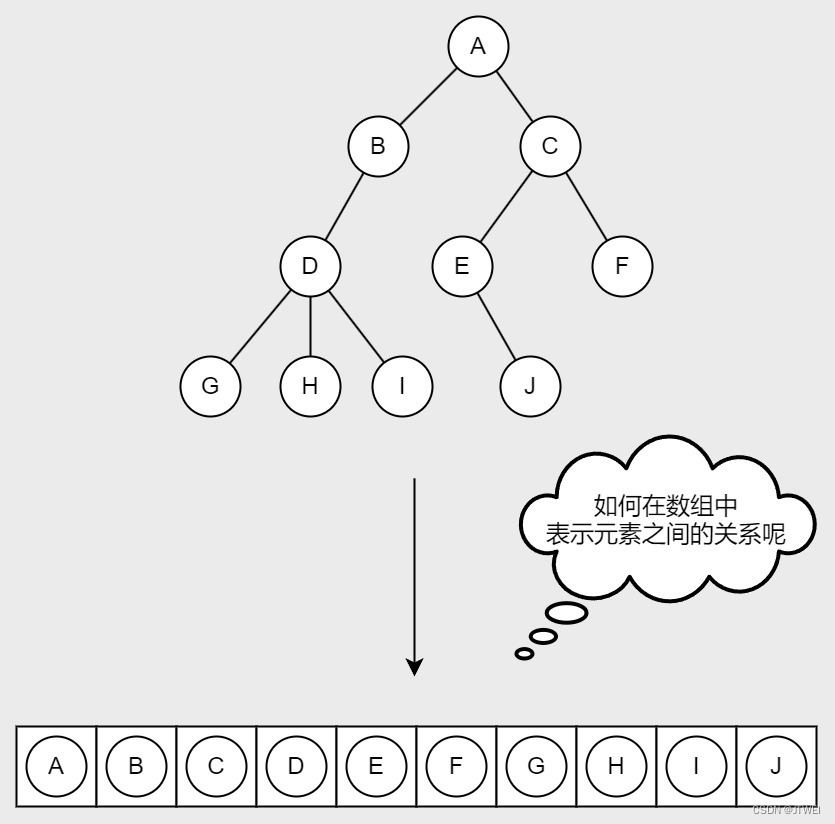
我们可以把上图中的树按照从上到下,从左到右的关系依次添加到数组中,但是如何各个元素之间的关系呢?
在树的定义中,我们强调了节点个数n>0时,根节点是唯一的。并且除了根节点之外,每个节点都有父节点(parent)。所以通过在元素中增加parent的下标,就可以知道当前节点的父节点是谁了。因为根节点没有父节点,所以约定根节点的parent=-1。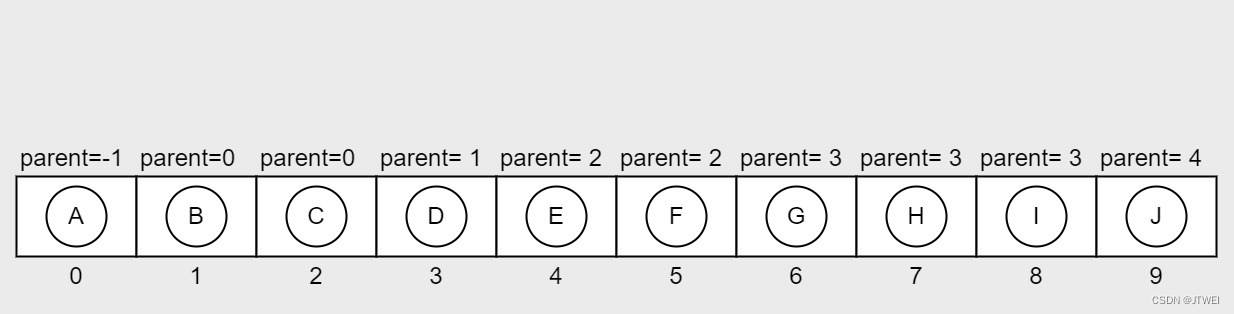
这样的存储结构,我们可以 根据节点的parent指针很容易找到它的双亲,时间复杂度为O(1),直到parent为-1时,表示找到了树的根节点。可是如果我们要知道节点的孩子是什么,应该怎么办呢?
同样的思路,我们可以增加一个孩子节点。这样我们就可以知道当前节点的孩子了。这个时候,可能会问,如果有多个孩子应该怎么办呢?我们的第一反应是可以用数组,这个方法当然可以,但是有更好的办法。
我们增加一个节点最左边孩子的指针域,不妨叫它长子域。如果没有孩子的节点,这个长子域就设置为-1.再添加一个右兄弟的指针域,这样不管有多少孩子,我们都可以通过不断查找有兄弟的方法,找到左右的孩子。以G、H、I为例,G为长子,H为G的右兄弟,I为H的有兄弟。
我们把上边提到的结构汇总成一张表格,通过表格,我们就可以知道所有节点之间的关系了。
| data | 下标 | parent | firstChild | rightSibling |
| A | 0 | -1 | 1 | -1 |
| B | 1 | 0 | 3 | 2 |
| C | 2 | 0 | 4 | -1 |
| D | 3 | 1 | 6 | -1 |
| E | 4 | 2 | 9 | 5 |
| F | 5 | 2 | -1 | -1 |
| G | 6 | 3 | -1 | 7 |
| H | 7 | 3 | -1 | 8 |
| I | 8 | 3 | -1 | -1 |
| J | 9 | 4 | -1 | -1 |
以下是完整的代码:
public class TreeNode<T>
{
public T Data { get; set; }
public int Index { get; set; }
public int ParentIndex { get; set; }
public int FirstChildIndex { get; set; }
public int RightSiblingIndex { get; set; }
public TreeNode(T data, int index, int parentIndex, int firstChildIndex, int rightSiblingIndex)
{
Data = data;
Index = index;
ParentIndex = parentIndex;
FirstChildIndex = firstChildIndex;
RightSiblingIndex = rightSiblingIndex;
}
}
public class Tree<T>
{
private TreeNode<T>[] nodes;
public Tree()
{
nodes = new TreeNode<T>[10];
}
// 添加节点
public void AddNode(T data, int index, int parentIndex, int firstChildIndex, int rightSiblingIndex)
{
var node = new TreeNode<T>(data, index, parentIndex, firstChildIndex, rightSiblingIndex);
nodes[index] = node;
}
// 获取根节点
public TreeNode<T> GetRoot()
{
return nodes[0];
}
// 获取某节点的子节点
public TreeNode<T> GetFirstChild(TreeNode<T> node)
{
if (node.FirstChildIndex == -1)
return null;
return nodes[node.FirstChildIndex];
}
// 获取某节点的右兄弟节点
public TreeNode<T> GetRightSibling(TreeNode<T> node)
{
if (node.RightSiblingIndex == -1)
return null;
return nodes[node.RightSiblingIndex];
}
}
孩子表示法
具体办法是,把每个节点的孩子节点排列起来,以单链表作为存储结构,则n个节点有n个孩子链表,如果是叶子节点则次单链表为空。然后n个头指针又组成一个线性表。采用顺序存储结构,存放在一个一维数组中。
为此,设计两种节点结构。
结构一:表头数组的表头节点。其中data是数据域,存储某节点的数据信息。firstchild是头指针域,存储该节点的孩子链表的头指针。
结构二:孩子链表的孩子节点。其中,child用来存储某个节点在表头数组中的下标。next是指针域,用来存储指向某节点的下一个孩子节点的指针。
//孩子节点
class ChildNode
{
int parentIndex;
ChildNode? next;
}
//表头结构
class HeadArray<T>
{
T data;
ChildNode? firstChild;
}
//树结构
internal class ChildDescribingTree
{
//节点数组
HeadArray<string>[]? nodes;
//根的位置
int? index;
//节点数
int? count;
}这样的结构对于我们要查某个节点的某个孩子,或者找某个节点的兄弟,只需要查找这个节点的孩子单链表即可。对于遍历整棵树也是很方便的,对于节点的数组循环即可。
但是这也存在着问题,我们如何知道某个节点的双亲是谁呢?比较麻烦,需要整棵树遍历才行。所以把双亲表示法和孩子表示法结合一下。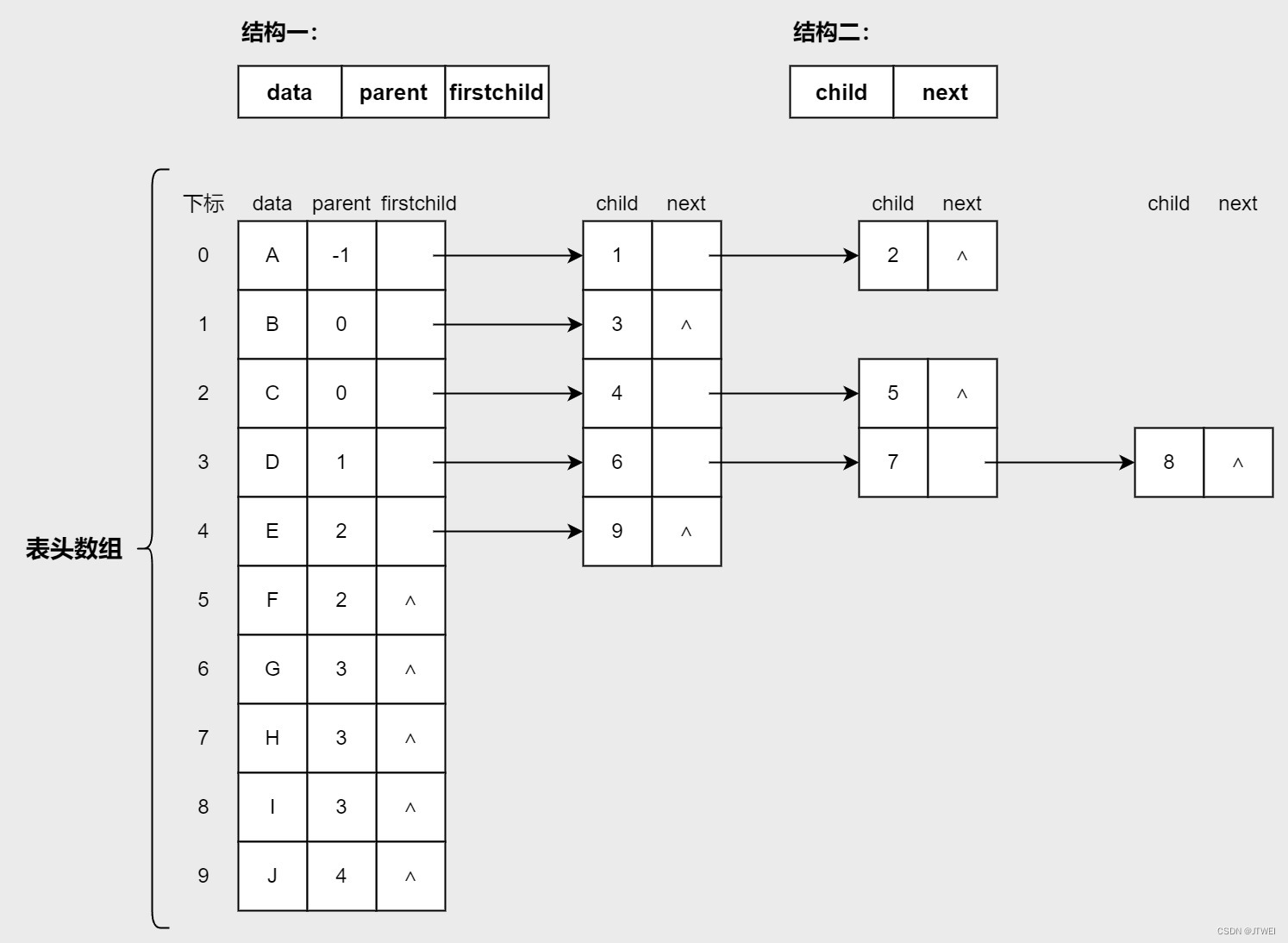
//孩子节点
class ChildNode
{
int parentIndex;
ChildNode? next;
}
//表头结构
class HeadArray<T>
{
T data;
int parent; //只需要在这里记录下父节点的下标即可。
ChildNode? firstChild;
}
//树结构
internal class ChildDescribingTree
{
//节点数组
HeadArray<string>[]? nodes;
//根的位置
int? index;
//节点数
int? count;
}孩子兄弟表示法
以上两种表示方法,分别从双亲的角度和孩子的角度研究树的存储结构,如果我们从树节点的兄弟的角度考虑又会如何呢?我们观察后发现,任意一棵树,它的节点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该节点的第一个孩子和此节点的有兄弟。这种表示方法,给查找某个节点的某个孩子带来了方便。只需要通过firstchild找到此节点的长子,然后通过长子节点的右孩子找到他的二弟,接着一直往下找,直到找到具体的孩子。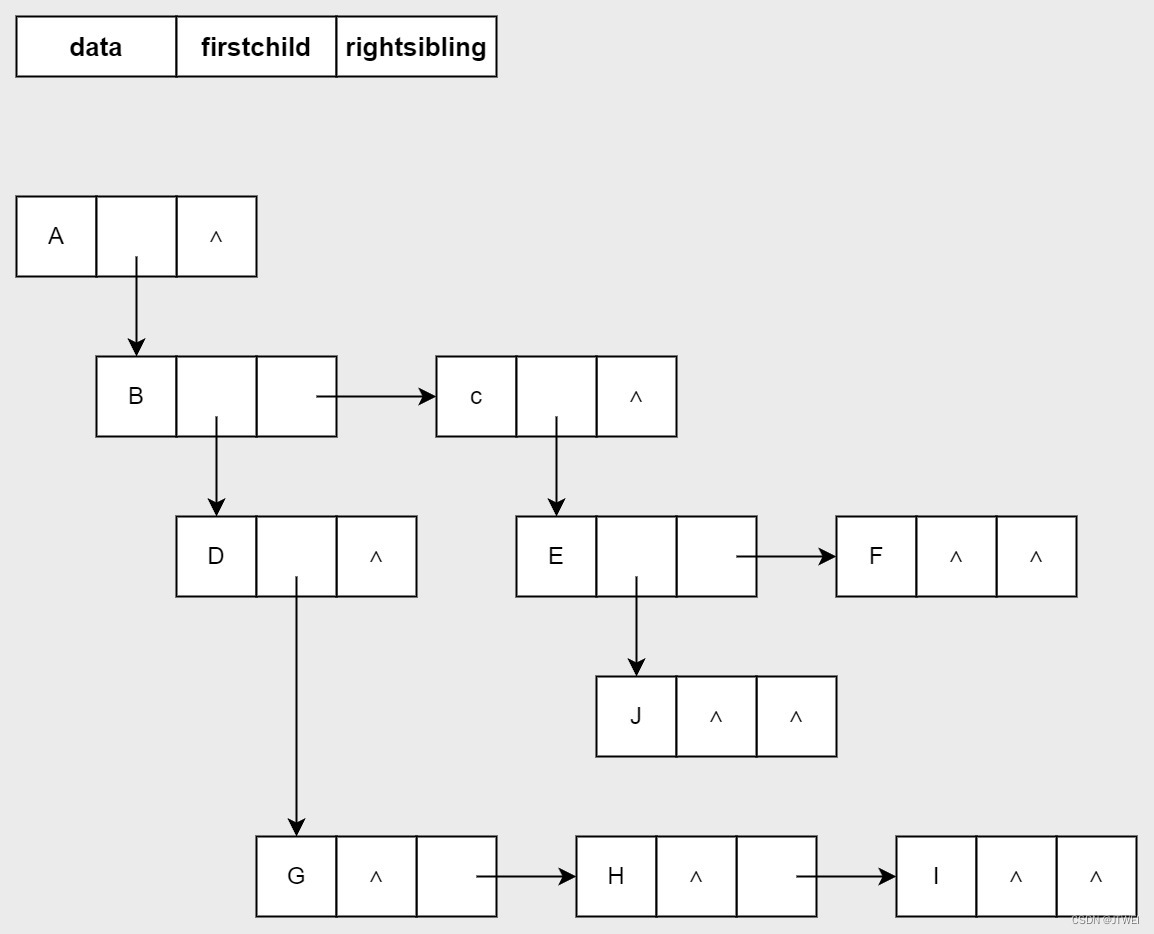
其实这种表示法最大的好处是它把一棵复杂的树变成了一棵二叉树。
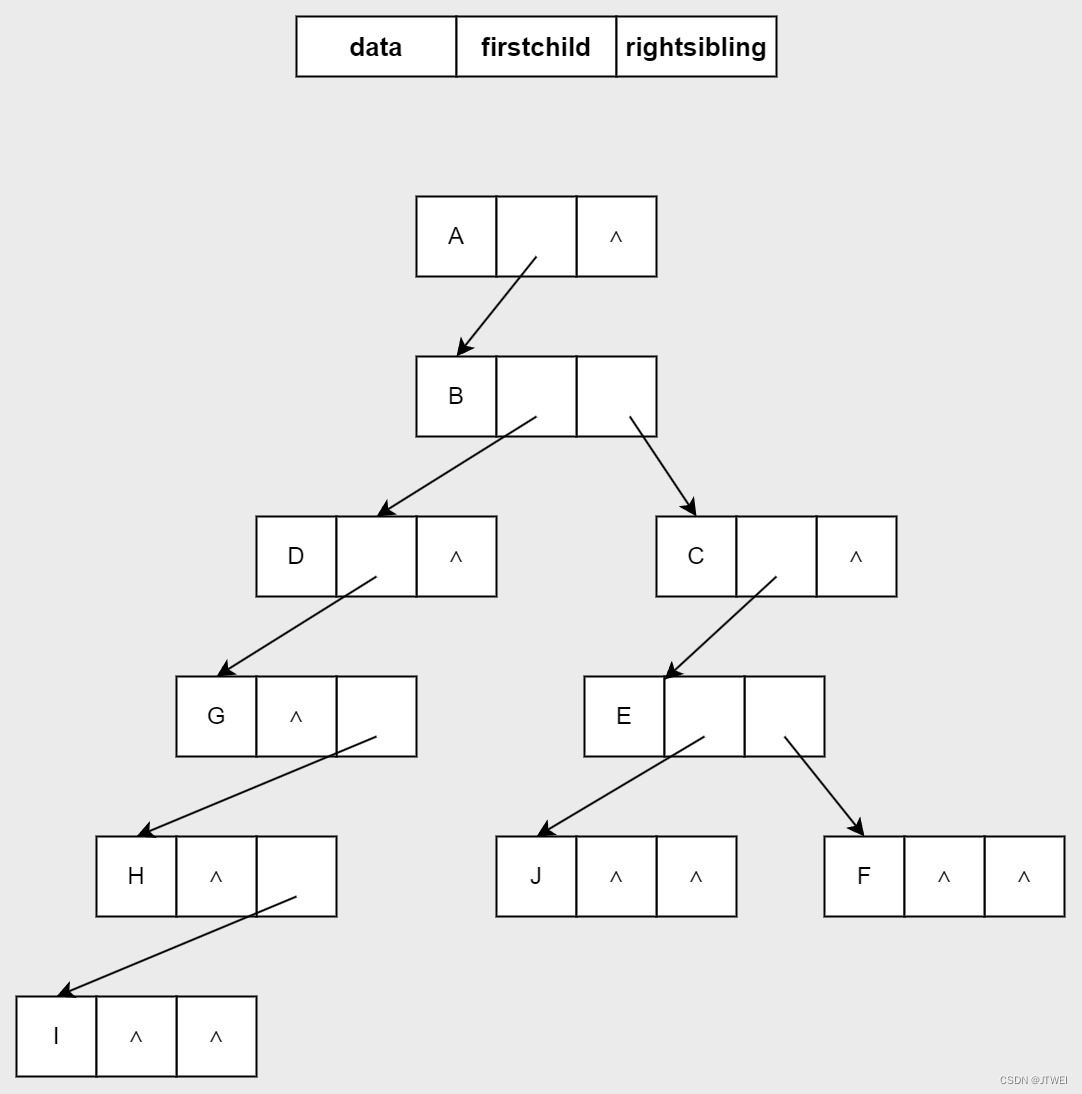
在树的结构中,最重要最常用的就是二叉树。接下来,我们将学习集中常用的二叉树。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








