移动次数
假设将n块从原始位置移动到目标位置需要An步,
将n-1块从A借助C移动到B,再从B借助A移动到C 则需要2A(n-1)步,加上剩下一块移动一步,可得
An = 2A(n-1)+1
将An+1视为以2为公比的等比数列
An+1 = 2*[A1(n-1)+1]
An+1 = 2*2^(n-1)
即An = 2^n -1
/**
* :汉诺塔问题
* @author DUSTDAWN
*
*/
public class Solution_8 {
/**
* a:起点位
* b:辅助位
* c:目标位
*/
static int count = 0;
/*
* 递归实现
*/
public static void Hanoi(int n,char a,char b,char c) {
if(n==1)
move(a,c);
else {
//第一步:将n-1块看作整体从起点位a,
//借助辅助位"c",放入终点位b中
Hanoi(n-1,a,c,b);
//把1从起点位放入终点位c
move(a,c);
//第二步:将n-1块看作整体从起点位b
//借助辅助位a 放入终点位c中
Hanoi(n-1,b,a,c);
}
}
/*
* :非递归通过栈实现
*
*/
public static void Hanoi2(int n,char a,char b,char c) {
StateStack stateStack = new StateStack();
stateStack.push(new State(n,a,b,c));
State state = null;
while((state = stateStack.pop())!=null) {
if(state.N == 1)
move(state.A,state.C);
else {
//逆序,先进后出,后出顺序与递归顺序一致
stateStack.push(new State(state.N-1,state.B,state.A,state.C));
stateStack.push(new State(1,state.A,state.B,state.C));
stateStack.push(new State(state.N-1,state.A,state.C,state.B));
}
}
}
/**
* :单步移动
*/
public static void move(char source, char target) {
System.out.println(source+"-->"+target);
count++;
}
public static void main(String[] args) {
// Hanoi(3,'A','B','C');
Hanoi2(3,'A','B','C');
System.out.println(count);
}
}
class State {
public int N;
public char A;
public char B;
public char C;
public State(int n, char a, char b, char c) {
N = n;
A = a;
B = b;
C = c;
}
}
class StateStack{
private State[] state = new State[1000];
private int top = 0;
public void push(State state) {
this.state[top++] = state;
}
public State pop() {
if(top>0)
return state[--top];
else
return null;
}
}
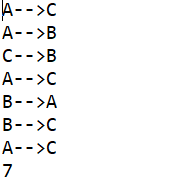





 本文详细解析了汉诺塔问题的数学模型,介绍了通过递归和非递归方式解决汉诺塔问题的方法,并提供了具体的Java代码实现。文章展示了如何计算移动次数以及不同策略下的移动步骤。
本文详细解析了汉诺塔问题的数学模型,介绍了通过递归和非递归方式解决汉诺塔问题的方法,并提供了具体的Java代码实现。文章展示了如何计算移动次数以及不同策略下的移动步骤。
















 1944
1944

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








