Adversarial Visual Robustness by Causal Intervention论文笔记-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_37734256/article/details/121802933

本文介绍了一种名为CiiV的框架，旨在提升深度学习模型对对抗样本的鲁棒性。不同于对抗训练，CiiV采用主动防御策略，仅使用正常样本进行训练，通过RetinotopicSampling操作引入工具变量，减少混杂因子的影响。实验表明，这种方法能有效防御不同攻击方法产生的对抗样本，且在保持模型预测准确性的同时增强其稳定性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

简介

文章解决的问题： 提升模型对于对抗样本的鲁棒性
对抗训练劣势： 大部分有效的防御方法仍然是对抗训练。而对抗训练是否有效，又取决于是否有尽可能多的，来自不同攻击方法产生的对抗样本。由于是被动防御，因此无法免疫未知攻击
该方案优势： 是主动防御的训练方案，不需要模型进行无休止的对抗训练，而且训练时只使用了正常样本，没有使用对抗样本
文章的贡献： 分析了现有对抗性攻击和防御方法起作用的原因，并首次从因果推理的角度提出了一种提升视觉模型鲁棒性的训练方法，可有效地防御来自不同攻击方法产生的对抗样本

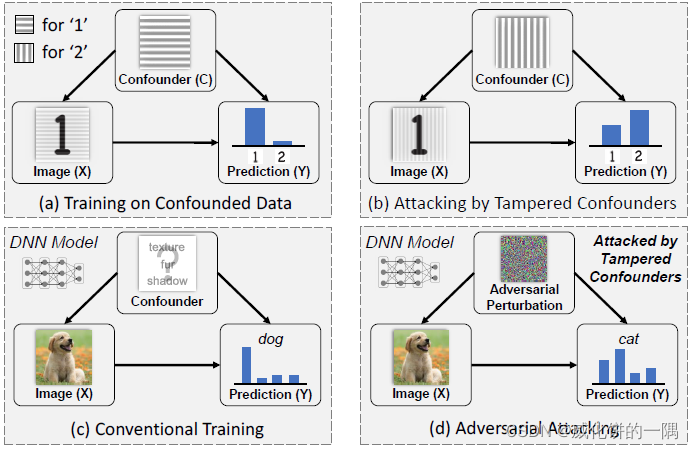
在这里插入图片描述

motivation

AI会利用人看不见的模式进行分类，这些模式组成混杂因子(confounder)，例如上图中作为背景的条纹，数字1的背景大部分是横的条纹，数字2的背景大不符恩是竖着的条纹。因为DNN基于输入和输出的统计联系进行学习，DNN不可避免地学习到了这种虚假的关联。如果训练数据和测试数据分布一样，这种混杂对于分类是有利的；但是如果这种模式被攻击者篡改，比如把数字1的背景换成竖着的，实现对抗攻击，这种混杂就是有害的。对抗训练常用于防御对抗样本，但它无法免疫未知的攻击。在现实中，移除未观测到的、未知的混杂因子是困难的。
原始数据 $X$ 和预测 $Y$ 的总效应和因果效应分别为 $P (Y ∣ X)$ 和 $P (Y ∣ d o (X = x))$ ，后门路径 $\leftarrow C \rightarrow Y$ 的存在导致二者的差异，差异为混杂效应。生成对抗样本的过程中，用 $\delta$ 表示对抗性扰动， $f_i(\cdot)$ 和 $f_j(\cdot)$ 分别表示DNN在类别 $i$ 和类别 $j$ 的输出值。对抗样本攻击中，有目标攻击 $\bar{y}$ 是一个预先指定的值，而无目标攻击是要分类错误 $\bar{y} \neq y$ 即可。
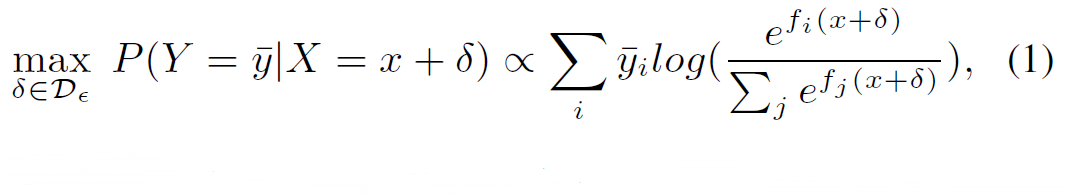
在这里插入图片描述
合法的 $D_\epsilon$ 或保留语义特征（负责对抗样本也欺骗了人眼），也就是说 $\delta$ 捕获改变因果特征， $P (Y ∣ d o (X = x))$ 不会改变，因而对抗样本攻击实际上是在通过最大化混杂效应来优化 $P (Y ∣ X)$ ，实现 $Y=\bar{y}$ 。

对现有攻防的分析

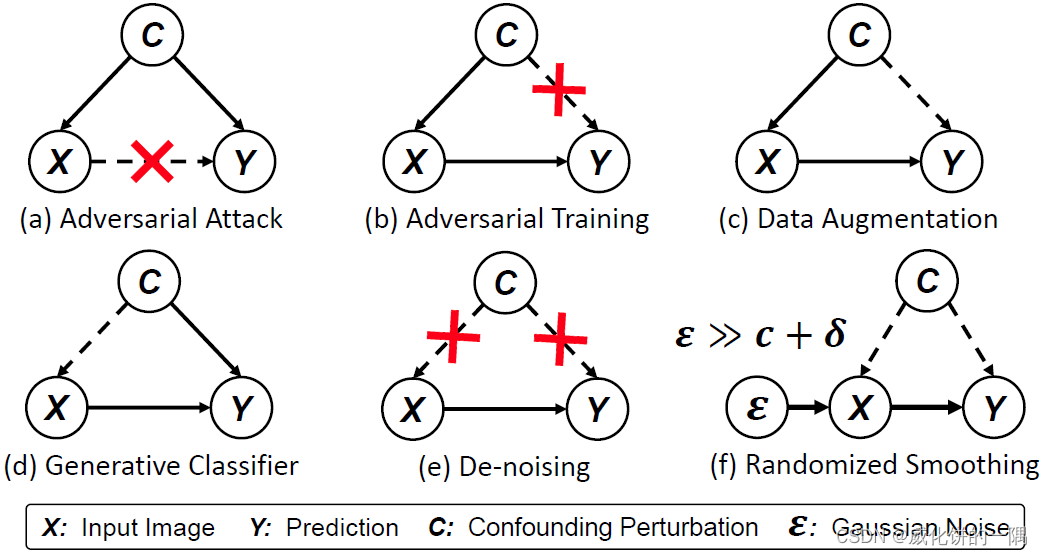
在这里插入图片描述

对抗样本攻击： 通过最大化混杂效应 $\leftarrow C \rightarrow Y$ 来覆盖 $\rightarrow Y$ ，让预测出错
对抗训练： 使用对抗样本训练模型，最大化在有攻击 $X=x+\delta$ 下的模型预测准确率。因为攻击时使用的与训练时使用的对抗样本相似，对抗训练防止混杂 $\delta$ 改变预测结果，阻断了 $\nrightarrow Y$
数据增强： 例如，用不同样本的线性组合来训练模型，增强鲁棒性，让微小的扰动 $\delta$ 只会产生较小的混杂效应，削弱 $\rightarrow Y$ 的连接
生成模型： 使用生成式的模型，例如用VAE式的模型，在预测时寻找哪一个类别 $y_i$ 最有可能产生能代表输入 $x$ 的样本，生成的过程削弱了混杂因子在原图中的影响 $\nrightarrow X$
去噪： 去除噪声对原图 $\nrightarrow X)$ 或者预测结果 $\nrightarrow Y)$ 的影响
随机平滑： 加入足够大的高斯噪声，覆盖自然的和攻击的混杂影响 $c+\delta$

CiiV框架

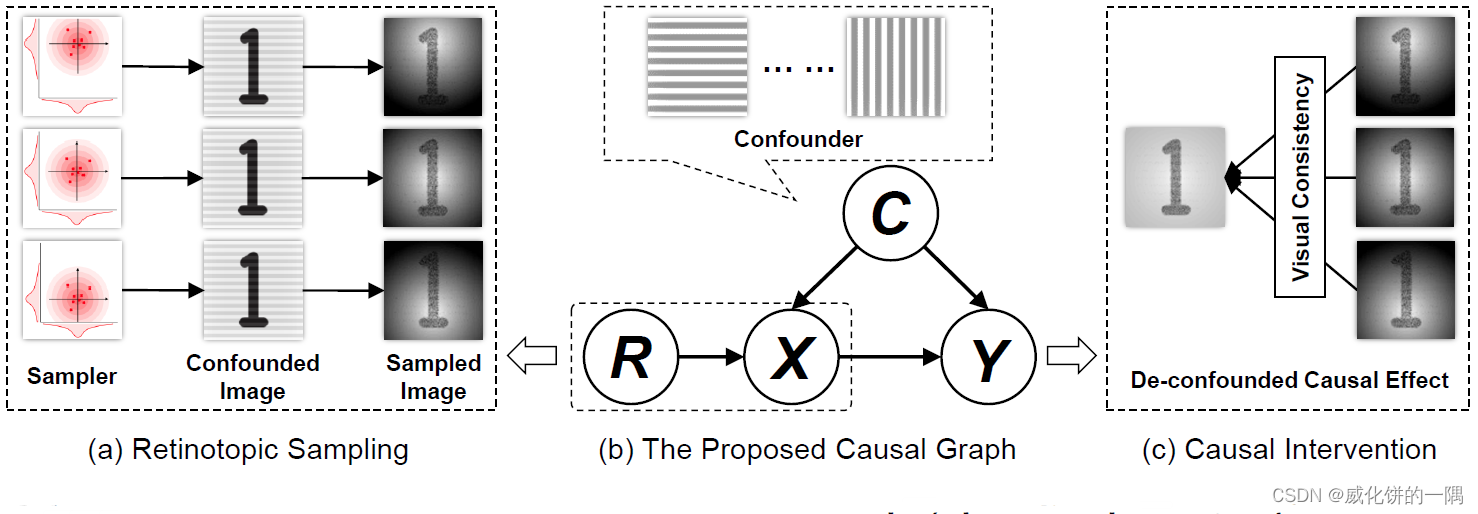
在这里插入图片描述
文中提出了CiiV框架，训练出鲁棒的模型，相比于正常的模型，训练过程中只多了Retinotopic Sampling操作。该操作将引入工具变量，进行干预的操作进行了实现。要实现，包含 $g_{rx}(\cdot)$ ， $g_{ry}(\cdot)$ 和 $g_{rx}^{-1}(\cdot)$ 三个部分。
在这里插入图片描述
具体而言， $g_{rx}(\cdot)$ 为Retinotopic Sampling采样操作，采样的分布为 $r$ ，输入为样本 $x$ ，输出为 $x_r=g_{rx}(x,r)$ , $\bigodot$ 表示元素相乘，采样操作在给定的分布 $r$ 下执行 $N$ 次取平均：
$g_{rx}(x,r)=r \bigodot \frac{1}{N}\sum_{i}ReLU([\frac{x+\epsilon_i}{|x+\epsilon_i|_{dt}};\frac{x-\epsilon_i}{|x-\epsilon_i|_{dt}}])$
采样操作实现的效果是，对 $r$ 分布的中间关注更多，对周围的关注变少。而 $g_{ry}(\cdot)$ 可以为任意的一个神经网络表示，只需要加上上面的采样操作层即可。
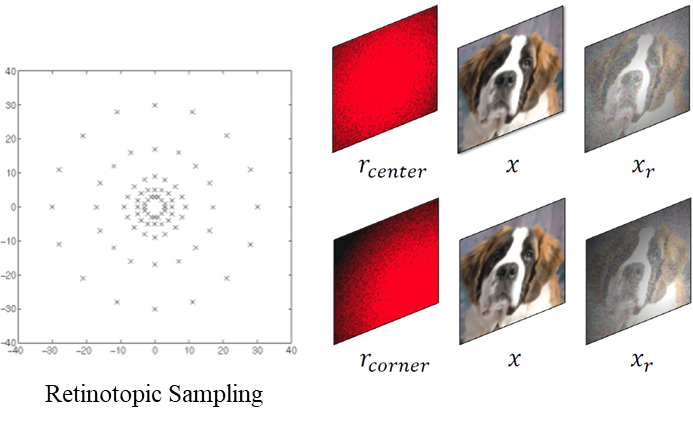
在这里插入图片描述
文中认为， $g_{rx}(\cdot)$ 是采样操作，其逆操作 $g_{rx}^{-1}(\cdot)$ 是集成操作，也就是求 $T_r$ 个 $r$ 分布采样后的平均，其中 $T_r$ 表示采样操作中使用的𝑟分布的个数，训练阶段 $T_r=10$ ，预测阶段 $T_r=1$
$P(Y|do(X=x))=g_{rx}^{-1}(g_{ry}(x,r)) \approx \frac{1}{T_r} \sum_r g_{ry}(x,r)$
最后，使用神经网络加上采样层来拟合上式 $\rightarrow Y$ ，使用交叉熵损失即可。特别的，由于训练过程不稳定，文中提出在交叉熵损失基础上，使用AVC loss
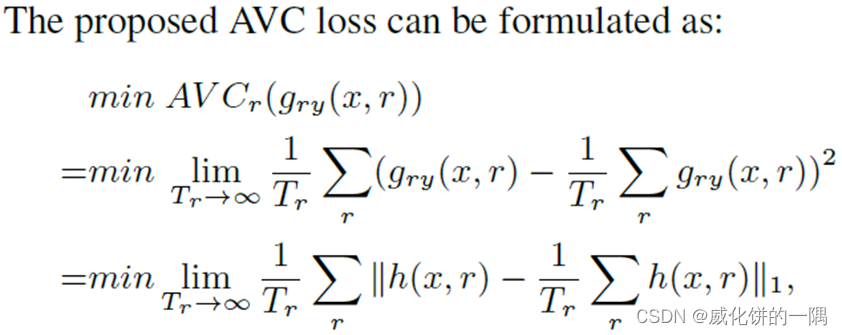
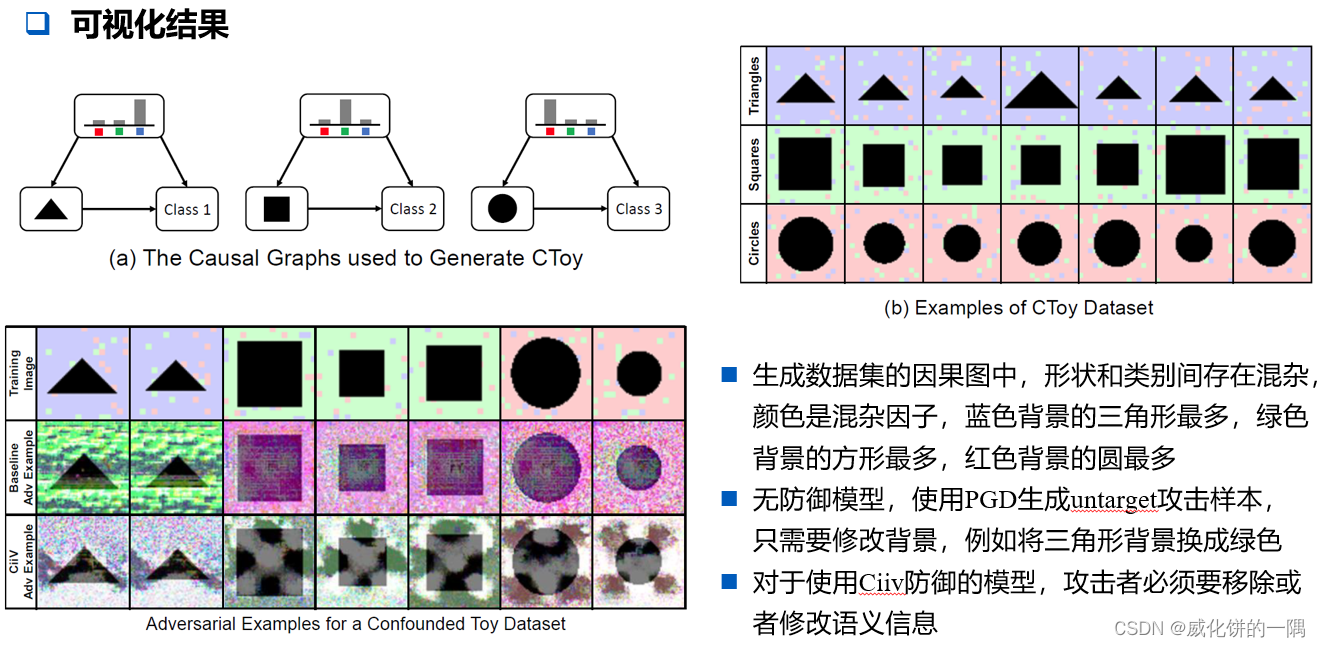
在这里插入图片描述