二叉树操作篇 -- 判断是否为二叉搜索树的后续遍历序列_二叉搜索树后序遍历判断-优快云博客

题目描述

牛客网：JZ23 二叉搜索树的后续遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。（ps：我们约定空树不是二叉搜索树）
示例

输入：[4,8,6,12,16,14,10]
输出：true
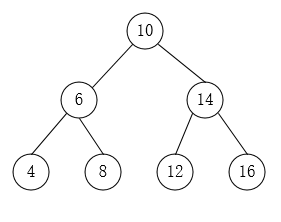
下图为后序遍历的一种二叉搜索树：

题目解析

方法一：递归

二叉搜索树的定义为根节点大于左子树节点，小于右子树节点，中序搜索的结果为非递减序列。

题目给出后续遍历序列，后续遍历顺序为左 - 右 - 根，因此，序列的最后一个元素就是当前树的根节点。
找到根节点后，再遍历序列，找到右子树的开始位置，将整个序列划分为：左子树 + 右子树 + 根。
若满足左子树皆小于根节点、右子树皆大于根节点，再分别判断左右子树是否满足条件，直至只剩一个节点，视为满足题意。

以上述示例为例具体分析：
对于给出的序列[4,8,6,12,16,14,10]

确定根节点，为序列最后元素10
后序遍历序列先左子树后右子树，左子树小，右子树大，因此遍历序列找到第一个大于根节点的数，即为右子树的开始，为12
由此，树的结构为：左[4,8,6],右[12,16,14],根[10]
对其左右子树继续相同操作：
左子树可分为：左[4],右[8],根[6]
右子树可分为：左[12],右[16],根[14]
当序列中只有一个节点时，停止递归，返回结果。

上述思路采用分支思想，将问题不断划分为子问题，具体实现采用递归算法。

public boolean VerifySquenceOfBST(int [] sequence) {
        int n = sequence.length;
        // 空树不为二叉树
        if(n <= 0){
            return false;
        }
        return isPost(sequence,0,n - 1);
    }
    public boolean isPost(int[] seq,int start,int end){
        // 只有一个节点
        if(start >= end){
            return true;
        }
        // 数组尾部为根节点
        int root = end;
        // 寻找右子树的位置
        int right = start;
        while(right < root && seq[right] < seq[root]){
            right++;
        }    
        // 判断右子树是否全部大于根节点
        for(int i = right;i < root;i++){
            if(seq[i] < seq[root]){
                return false;
            } 
        }
        // 分治法判断左右子树是否都满足条件
        return isPost(seq,start,right - 1) && isPost(seq,right,end - 1);
    }