7-4 斐波那契数 (20 分)
斐波那契数,亦称之为斐波那契数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、……,这个数列从第3项开始,每一项都等于前两项之和。这里我们定义另外一种斐波那契数列: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2)。编程计算该数列的前n(n<1000000)项是否能被3整除。
输入格式:
输入为一个正整数n(n<1000000)。
输出格式:
输出上述数列前n项能否被3整除,能则输出“yes ”,否则输出"no "。注意:每个"yes"和"no"后面都有一个空格。
输入样例1:
2
输出样例1:
no no
输入样例2:
6
输出样例2:
no no yes no no no
解析:其实是一道找规律题目,在比赛的时候直接按照常规斐波那契的思路处理的,结果导致在编译较大数的时候直接超时。
后来在赛场上也真是慌得一批,竟然还想着改造自己写的递归程序。直到比赛结束之后别人提醒才发现这是一道极其简单的找规律题。。
#include<iostream>
#include<cstdio>
using namespace std;
int main(){
int n;
scanf("%d",&n);
for(int i=0;i<n;i++ ){
if(i<2){
printf("no ");}
else if(i>=2){
if(i%4==2)
printf("yes ");
else
printf("no ");
}
}
return 0;
}
另附上超时代码:
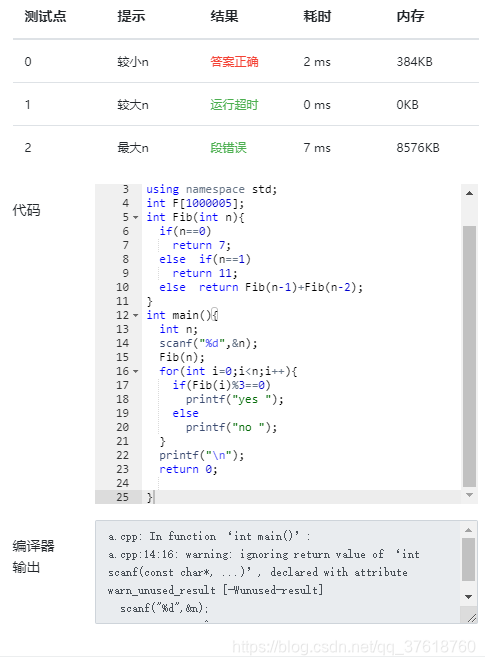








 本文探讨了一种变种斐波那契数列的计算问题,定义为F(0)=7,F(1)=11,后续项遵循斐波那契规则。文章通过观察发现了一个规律,即数列中特定位置的项能够被3整除,并提供了一段高效的C++代码实现,避免了直接计算带来的超时问题。
本文探讨了一种变种斐波那契数列的计算问题,定义为F(0)=7,F(1)=11,后续项遵循斐波那契规则。文章通过观察发现了一个规律,即数列中特定位置的项能够被3整除,并提供了一段高效的C++代码实现,避免了直接计算带来的超时问题。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








