本文介绍了支持向量机（SVM）的基本原理，包括如何定义最大间隔的超平面，以及如何通过拉格朗日乘子法转换为对偶问题。讨论了在特征空间中的映射和核函数的作用，常见核函数的选择，并介绍了软间隔的概念以应对非线性可分情况。此外，还探讨了正则化和不同的损失函数，如L1和L2范数，以及支持向量机在回归任务中的应用——支持向量回归（SVR）。
在样本空间中，划分超平面的线性方程为：
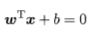
w为法向量，决定了超平面的方向；b为位移项，决定超平面与原点之间的距离。样本中任意点x到超平面(w,b)的距离为：
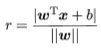
假设超平面能将训练样本正确分类
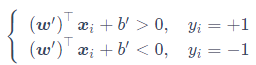
根据几何间隔，以上关系修正为
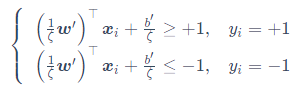
距离超平面最近的这几个训练样本点使上式成立，它们被称为支持向量，两个异类支持向量到超平面的距离之和为
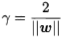
欲找到最大间隔的划分超平面，优化问题为
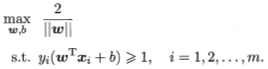
最大化问题转变为最小化
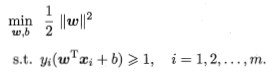
此为支持向量机的基本型。
上述本身是一个凸优化问题，可直接用现成的优化计算包求解，得到最大间隔划分超平面
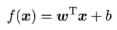
此优化可用拉格朗日乘子法得到其对偶问题，实现更高效。对每条约束添加拉格朗日乘子，该问题的拉格朗日函数可写为
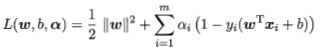
拉格朗日乘子法是一种寻找多元函数在一
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
