参考资料有邹博的机器学习PPT,七月在线第九期的PPT,这篇主要为学习笔记,对学到的内容进行总结与整理。
下面会介绍如下内容
- 从贝叶斯公式与极大似然估计
- 贝叶斯网络介绍与公式
- 三种条件独立图模型
- 贝叶斯网举例
- 有向分离分析
从贝叶斯公式与极大似然估计
给定样本DDD,求出一些结论 A1,A2,...,AnA_1,A_2,...,A_nA1,A2,...,An哪个是最可能的,也就是求 最大的P(Ai∣D)P(A_i|D)P(Ai∣D)所对应的 AiA_iAi,该AiA_iAi是最有可能的。
maxP(Ai∣D)=maxP(Ai,D)P(D)=maxP(D∣Ai)P(Ai)P(D)=maxP(D∣Ai)P(Ai)\max P(A_i|D)=\max \frac{P(A_i,D)}{P(D)}=\max \frac{P(D|A_i)P(A_i)}{P(D)}=\max P(D|A_i)P(A_i)maxP(Ai∣D)=maxP(D)P(Ai,D)=maxP(D)P(D∣Ai)P(Ai)=maxP(D∣Ai)P(Ai)
前两个等号是贝叶斯公式,最后一个等号成立是因为对于任意的AiA_iAi,分母都是一样而与AiA_iAi无关。
这里做个大胆的假设,假设取A1,,...,AnA_1,,...,A_nA1,,...,An的概率是相等的,那么我们得到:
maxP(Ai∣D)=maxP(D∣Ai)P(Ai)−>maxP(D∣Ai)\max P(A_i|D)=\max P(D|A_i)P(A_i)->\max P(D|A_i)maxP(Ai∣D)=maxP(D∣Ai)P(Ai)−>maxP(D∣Ai)
我们要求的是 maxP(Ai∣D)\max P(A_i|D)maxP(Ai∣D),实际计算的是 maxP(D∣Ai)\max P(D|A_i)maxP(D∣Ai),也就是在不同参数下P(D)P(D)P(D)最大值,这不就是极大似然估计么。
贝叶斯网络
把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中 G(V,E),就形成了贝叶斯网络。
- 其中每个节点表示随机变量 ViV_iVi
- 连接两个节点的箭头表示因果关系,被指向的节点是果,另外一个是因(父节点)
- 每个节点条件独立分布:P(Vi∣Vpa(i))P(V_i|V_{pa(i)})P(Vi∣Vpa(i)),Vpa(i)V_{pa(i)}Vpa(i)表示节点ViV_iVi的父节点。
贝叶斯网的联合分布公式为每个节点的条件概率连乘。
P(V1,V2,...,Vn)=∏i=1,2,...,nP(Vi∣Vpa(i))P(V_1,V_2,...,V_n)=\prod\limits_{i=1,2,...,n}P(V_i|V_{pa(i)})P(V1,V2,...,Vn)=i=1,2,...,n∏P(Vi∣Vpa(i))
P(a,b,c)=P(c∣a,b)P(b∣a)P(a)P(a,b,c)=P(c|a,b)P(b|a)P(a)P(a,b,c)=P(c∣a,b)P(b∣a)P(a)
显然,上式子是无条件成立的(贝叶斯公式),画成贝叶斯网则是下面的样子。
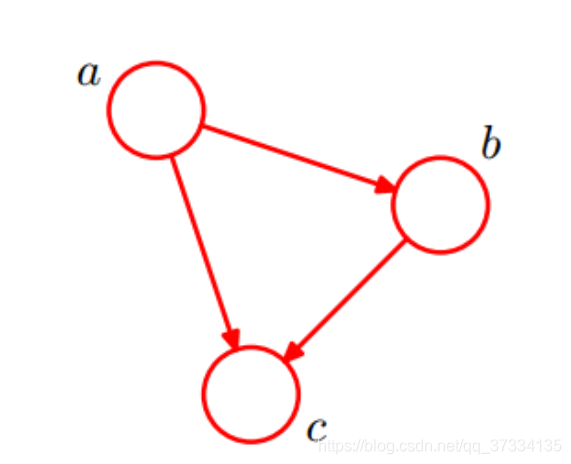
解释一下,aaa是没有任何箭头指向它的,所以直接写P(a)P(a)P(a),bbb由aaa指向它,根据定义则认为aaa是bbb父节点,那么bbb该条件概率分布为P(b∣a)P(b|a)P(b∣a),同样地,ccc同时由a,ba,ba,b指向,两者均为父节点,所以ccc节点的概率分为则为P(c∣a,b)P(c|a,b)P(c∣a,b),写在一起就是P(a,b,c)=P(c∣a,b)P(b∣a)P(a)P(a,b,c)=P(c|a,b)P(b|a)P(a)P(a,b,c)=P(c∣a,b)P(b∣a)P(a)。
补充:P(a,b,c)=P(c∣a,b)P(b∣a)P(a)P(a,b,c)=P(c|a,b)P(b|a)P(a)P(a,b,c)=P(c∣a,b)P(b∣a)P(a)如果推广到KKK 个节点则有
P(x1,...,xK)=P(xK∣x1,...,xK−1)...P(x2∣x1)P(x1)P(x_1,...,x_K)=P(x_K|x_1,...,x_{K-1})...P(x_2|x_1)P(x_1)P(x1,...,xK)=P(xK∣x1,...,xK−1)...P(x2∣x1)P(x1)
来看下面的贝叶斯网络,尝试写出联合分布P(x1,x2,...,x7)P(x_1,x_2,...,x_7)P(x1,x2,...,x7)
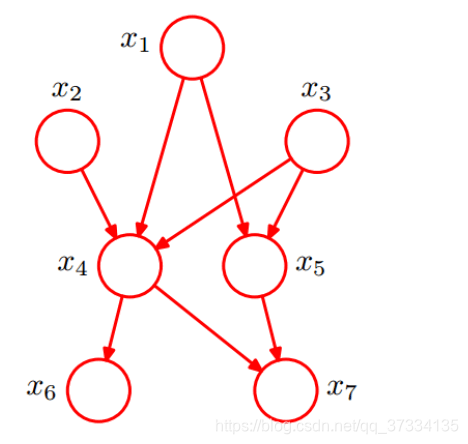
首先考虑节点x1,x2,x3x_1,x_2,x_3x1,x2,x3,这三个节点都没有箭头指向它们,所以是P(x1),P(X2),P(X3)P(x_1),P(X_2),P(X_3)P(x1),P(X2),P(X3);x4x_4x4均由x1,x2,x3x_1,x_2,x_3x1,x2,x3所指,所以就是P(x4∣x1,x2,x3)P(x_4|x_1,x_2,x_3)P(x4∣x1,x2,x3);x5x_5x5则由x1,x3x_1,x_3x1,x3指向,所以是P(x5∣x1,x3)P(x_5|x_1,x_3)P(x5∣x1,x3),同样地x6x_6x6的条件概率为P(x6∣x4)P(x_6|x_4)P(x6∣x4),x7x_7x7的条件概率为p(x7∣x4,x5)p(x_7|x_4,x_5)p(x7∣x4,x5),最后根据公式得到:
P(x1,x2,...,x7)=P(x1)P(X2)P(X3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)p(x7∣x4,x5)P(x_1,x_2,...,x_7)=P(x_1)P(X_2)P(X_3)P(x_4|x_1,x_2,x_3)P(x_5|x_1,x_3)P(x_6|x_4)p(x_7|x_4,x_5)P(x1,x2,...,x7)=P(x1)P(X2)P(X3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)p(x7∣x4,x5)
显然贝叶斯网络是非常直观的,那么它主要有什么好处呢,看下面的例子
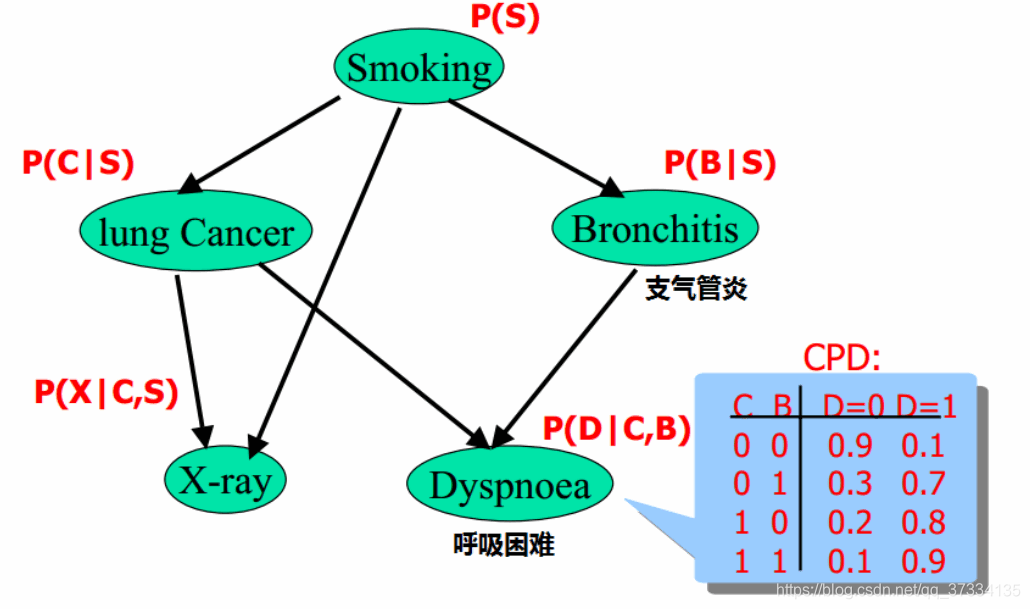
对于每个节点应该画出概率分布图,上面只写了呼吸困难的条件概率图,它只取决于是否得肺癌,是否有支气管炎,所以一共是2×2个参数,在图中已经列出。同样对于肺癌节点,只取决于是否吸烟,需要两个参数。对于整个图一共需要的参数是1+2+2+4+4=13,即只要13个参数就能求出P(S,L,B,X,D)P(S,L,B,X,D)P(S,L,B,X,D)。如果不做分析做出上面的贝叶斯网络,硬着求那么每个节点2种情况,5个节点就是252^525情况,需要252^525个参数,相差甚远。
贝叶斯网络例子
至今为止其实用了不少不贝叶斯网络了,比如前面学过的朴素贝叶斯,HMM,还有主题模型。
1、朴素贝叶斯作为贝叶斯网络
朴素贝叶斯给了一个很强的假设:给定类别yyy的条件下,特征x1,x2,...,xmx_1,x_2,...,x_mx1,x2,...,xm是条件独立的,对应的贝叶斯网络和公式如下:
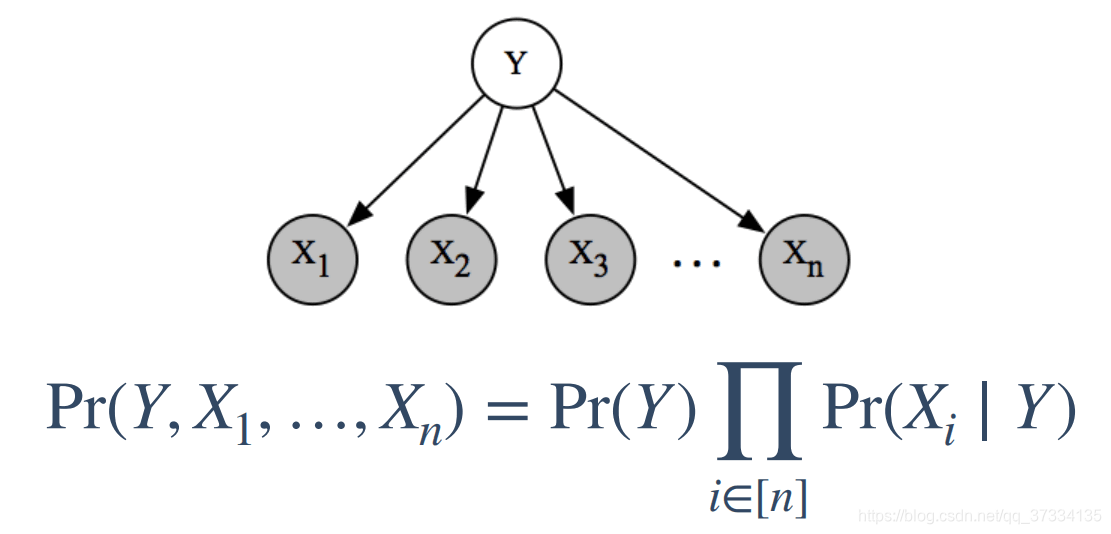
2、HMM作为贝叶斯网络
HMM也有两个假设:
- 齐次马尔可夫假设:任意时刻ttt的状态只与前一时刻t−1t-1t−1的状态有关,而与其他时刻状态、观测记忆时刻无关,即:
P(it∣it−1,ot−1,...,i1,o1)=P(it∣it−1)P(i_t|i_{t-1},o_{t-1},...,i_1,o_1)=P(i_t|i_{t-1})P(it∣it−1,ot−1,...,i1,o1)=P(it∣it−1) - 观测独立性假设: 任意时刻的状态只与该时刻马尔可夫链的状态有关,即:
P(ot∣iT,oT,...,i1,o1)=P(ot∣it)P(o_t|i_{T},o_{T},...,i_1,o_1)=P(o_t|i_{t})P(ot∣iT,oT,...,i1,o1)=P(ot∣it)
画成贝叶斯网,以及公式如下:
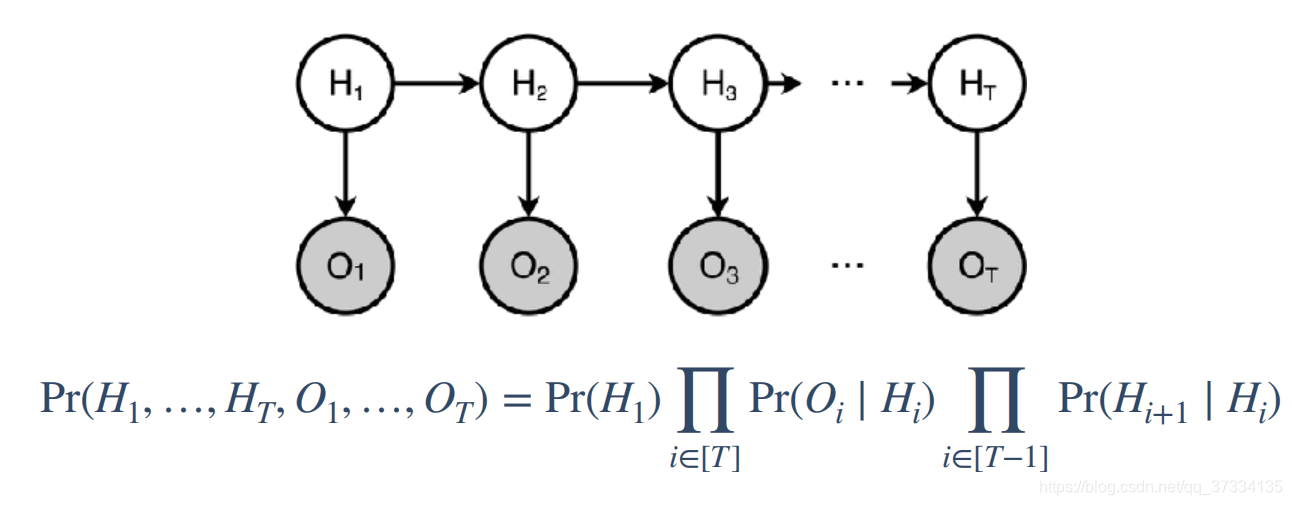
关于公式是怎么得来的呢,首先H1H_1H1是没有箭头指向的,所以条件概率就是P(H1)P(H_1)P(H1),对于任意的OiO_iOi都是由HiH_iHi指向的,所以条件概率是P(Oi∣Hi)P(O_i|H_i)P(Oi∣Hi),而对于任意的Hi+1H_{i+1}Hi+1都是由HiH_iHi指向的,所以是P(Hi+1∣Hi)P(H_{i+1}|H_{i})P(Hi+1∣Hi),所以最后得到了上面的式子。
通过贝叶斯网络判定条件独立的三种情况
通过贝叶斯网络判定条件独立的三种情况分别为:tail-to-tail,head-to-tail,head-to-head
介绍这三种情况之前,回顾一下随机变量独立和条件独立的公式。
(1)、A,B相互 独立
P(A,B)=P(A)P(B)P(A,B)=P(A)P(B)P(A,B)=P(A)P(B)
P(A∣B)=P(A)P(A|B)=P(A)P(A∣B)=P(A) (AAA是否发生与BBB没有任何关系)
P(B∣A)=P(B)P(B|A)=P(B)P(B∣A)=P(B)
(2)、A,B 条件独立
P(A,B∣C)=P(A∣C)P(B∣C)P(A,B|C)=P(A|C)P(B|C)P(A,B∣C)=P(A∣C)P(B∣C)
P(A∣B,C)=P(A∣C)P(A|B,C)=P(A|C)P(A∣B,C)=P(A∣C)
P(B∣A,C)=P(B∣C)P(B|A,C)=P(B|C)P(B∣A,C)=P(B∣C)
1、tail-to-tail
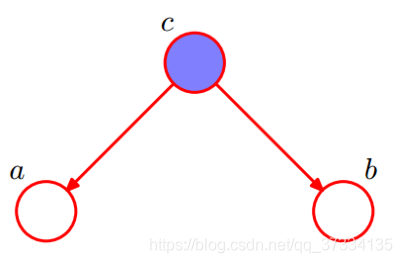
根据图模型得到:P(a,b,c)=P(c)P(a∣c)P(b∣c)P(a,b,c)=P(c)P(a|c)P(b|c)P(a,b,c)=P(c)P(a∣c)P(b∣c)
两边同除以P(c)P(c)P(c)得到:P(a,b∣c)=P(a∣c)P(b∣c)P(a,b|c)=P(a|c)P(b|c)P(a,b∣c)=P(a∣c)P(b∣c)
所以出在ccc给定情况下,a,ba,ba,b的条件独立的。
2、head-to-tail
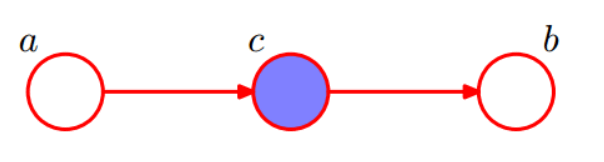
根据图模型得到:P(a,b,c)=P(a)P(c∣a)P(b∣c)P(a,b,c)=P(a)P(c|a)P(b|c)P(a,b,c)=P(a)P(c∣a)P(b∣c)
两边同除以P(c)P(c)P(c)得到:P(a,b∣c)=P(a)P(c∣a)P(b∣c)P(c)=P(c,a)P(b∣c)P(c)=P(a∣c)P(b∣c)P(a,b|c)=\frac{P(a)P(c|a)P(b|c)}{P(c)}=\frac{P(c,a)P(b|c)}{P(c)}=P(a|c)P(b|c)P(a,b∣c)=P(c)P(a)P(c∣a)P(b∣c)=P(c)P(c,a)P(b∣c)=P(a∣c)P(b∣c)
所以出在ccc给定情况下,a,ba,ba,b的条件独立的。
2、head-to-head
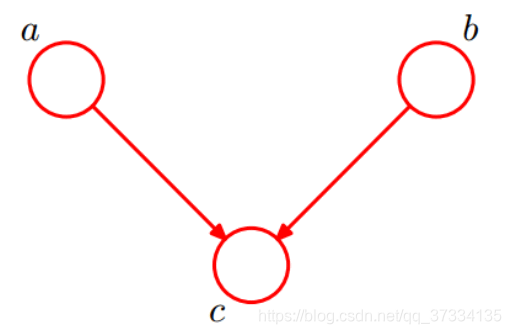
根据图模型得到:P(a,b,c)=P(a)P(b)P(c∣a,b)P(a,b,c)=P(a)P(b)P(c|a,b)P(a,b,c)=P(a)P(b)P(c∣a,b)
两把同时对ccc求和∑cP(a,b,c)=∑cP(a)P(b)P(c∣a,b)\sum\limits_{c}P(a,b,c)=\sum\limits_{c}P(a)P(b)P(c|a,b)c∑P(a,b,c)=c∑P(a)P(b)P(c∣a,b)
−>P(a,b)=P(a)P(b)->P(a,b)=P(a)P(b)−>P(a,b)=P(a)P(b)
所以得到,对ccc未知的情况下,a,ba,ba,b是相互独立的。
上述情况推广到节点集
若要A,BA,BA,B是条件独立的,需要满足有向分离,具体的定义说了可能也听不懂,具体的看下面的例子。
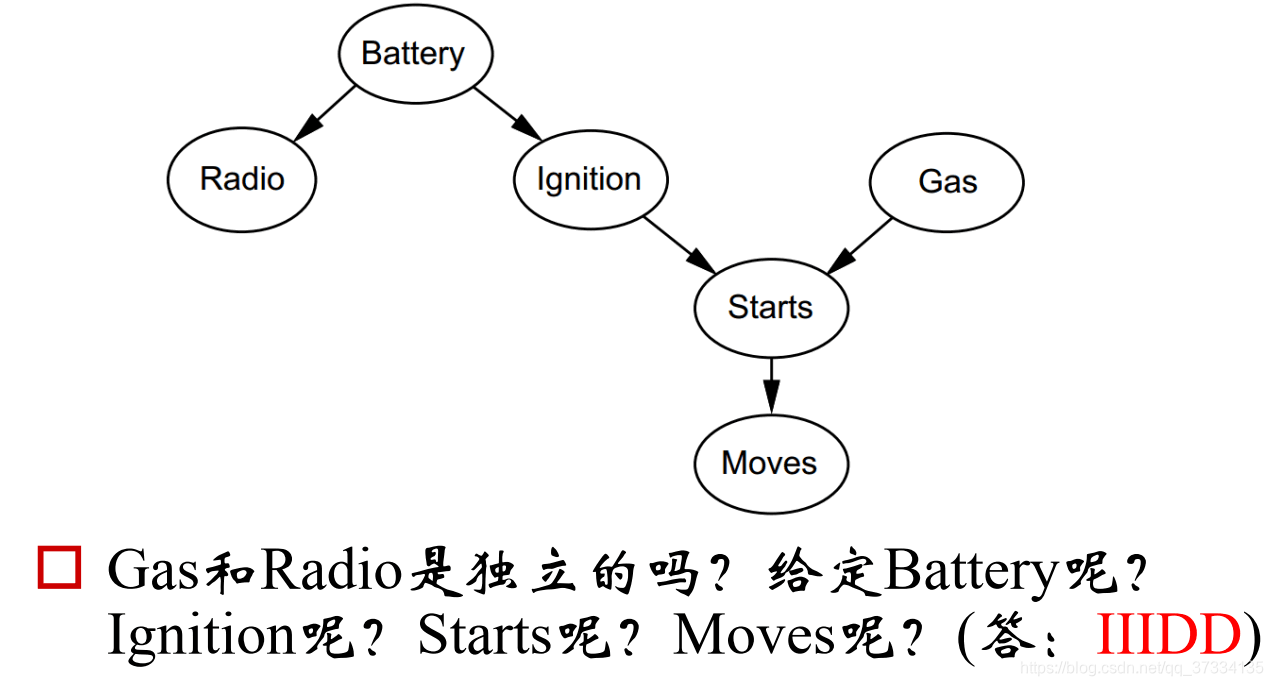
先回答第一个问题:Gas和Radio是独立的吗?
我们将(Radio,Battery,Ignition)看成一个节点,Gas看成一个节点,(Starts,End)看成一个节点,那么这时候这三个节点就满足上面介绍的head-to-head的情况,所以是独立的(大节点独立小节点也是独立的,不需要去考虑大节点的方向)。
给定Battery的话,将Battery看成一个节点,Radio看成一个节点,剩下的看成一个节点,此时满足tail-to-tail的情况,所以是条件独立的。
剩下的图中也给出了答案就不说了。





















 861
861

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








