机器学习之线性回归

线性回归

在机器学习中回归是求学者在学习过程中重要的一环。无论是面试还是实际应用都会经常用到。有很多人会使用线性回归，但却不知道线性回归是怎么来的。如果想让自己在机器学习的方向上更有价值，数学方面的推导必不可少。下面就是我在自己理解的线性回归推导。

什么是回归？

通过现有的数据最终预测出来在指定区间的某一个值 我们称之为回归

贷款栗子

解释

数据:

上图为五个人在银行贷款的样本，其中工资和年龄我们都称为特征(2个特征)

目标:

预测银行会贷款给我多少钱(标签)

考虑:

工资和年龄都会影响最终银行贷款的结果,那么他们各自有多大的影响呢(参数)

通俗解释:

X1,X2就是我们的两个特征(年龄，工资) Y是银行最终借给我们多少钱
找到最合适的一条线来最好的拟合我们的数据点

数学来了

假设 Θ1是年龄的权重， Θ2是工资的权重，Θ0是偏置项

拟合的平面:

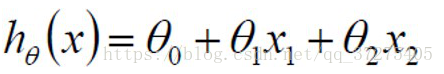
整合:

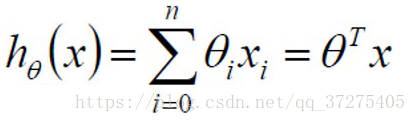
误差

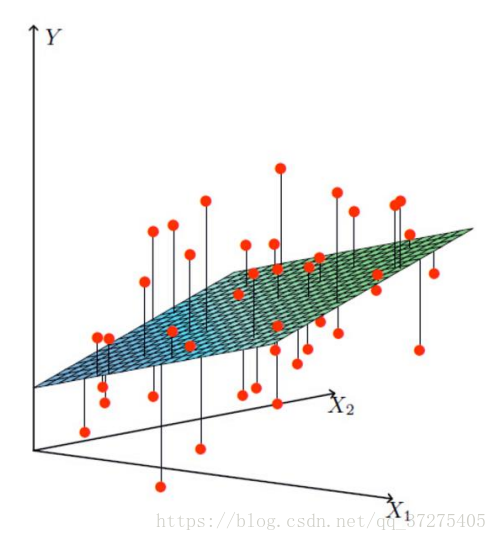
真实值和预测值之间肯定是要存在差异的(用 ε来表示该误差)

对于每个样本方程:

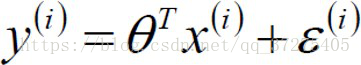
误差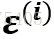是独立并且具有同分布，并且服从均值为0方差为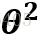的高斯分布

独立:张三和李四一起来贷款，他俩都是独立的互不影响

同分布:张三和李四来的都是在同一家银行贷款 用的用一套贷款算法

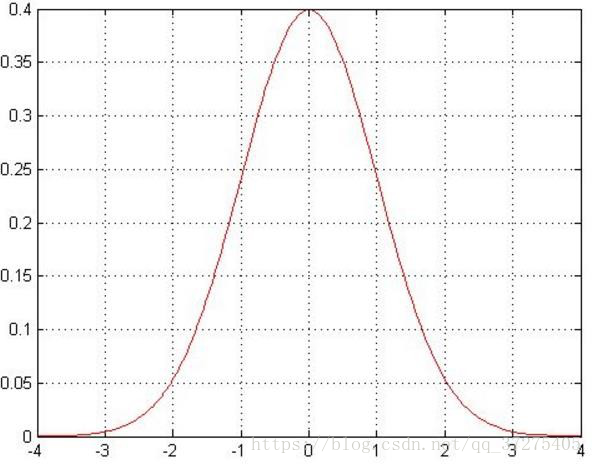
高斯分布:银行可能会多给，也可能会少给，但是绝大多数情况下这个浮动不会太
大，极小情况下浮动会比较大，符合正常情况

误差服从高斯分布:

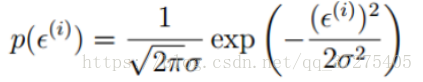
将预测值式子带入高斯分布式子:

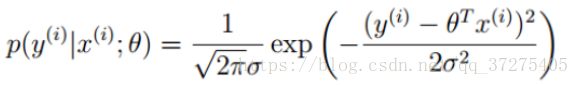
似然函数(最大似然估计)：

似然函数的理解:

什么样的数据跟参数组合后成为真实值的概率最大

方程:

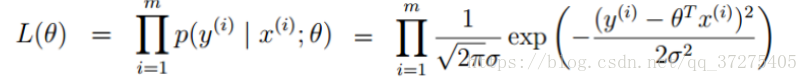
对数似然:

为什么会用到对数似然

乘法难解,加法就容易了，对数里面乘法可以转换成加法

方程:

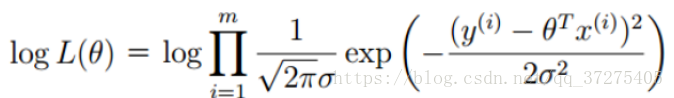
化简:

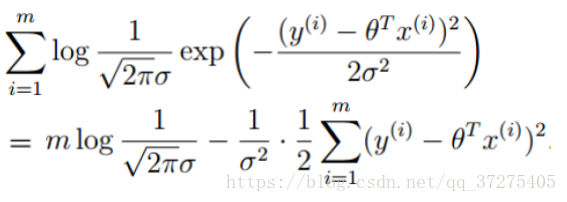
目标函数:

让似然函数(对数变换后也一样)越大越好 让预测值成为真实值得可能性越大越好（最小二乘法）

展开转置成自身

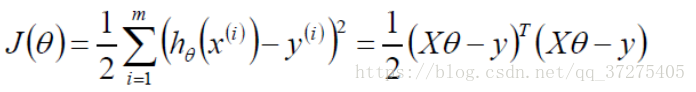
求偏导:

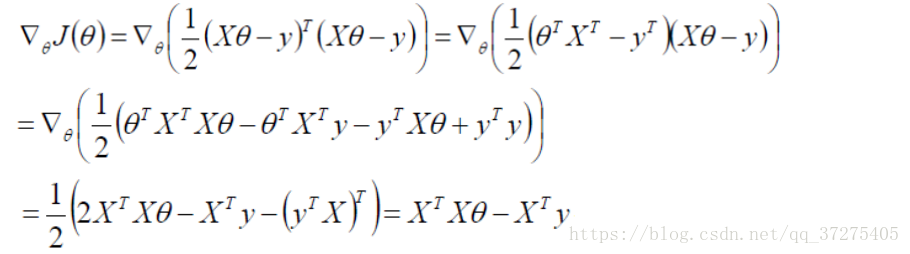
什么样的Θ能够使得整体的表达式的值越小越好（极小值点）
偏导等于0的位置满足这个条件

偏导等于0：

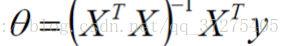
评估方法

最常用的评估项：

残差平方和:预测值和真实值之间的差异
R方约等于1：好
R方约等于0：不好