HDOJ1301“Jungle Roads”

最新推荐文章于 2018-09-29 12:04:20 发布

那就可爱多一点点

最新推荐文章于 2018-09-29 12:04:20 发布

阅读量147

点赞数 1

CC 4.0 BY-SA版权

分类专栏：算法

本文链接：https://blog.youkuaiyun.com/qq_37241934/article/details/81128099

算法专栏收录该内容

21 篇文章

订阅专栏

本文详细介绍了如何使用Prim算法解决最小生成树问题，并提供了一段完整的C++代码实现。通过实例输入输出展示算法的应用场景，适合初学者学习图论及最小生成树相关概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1301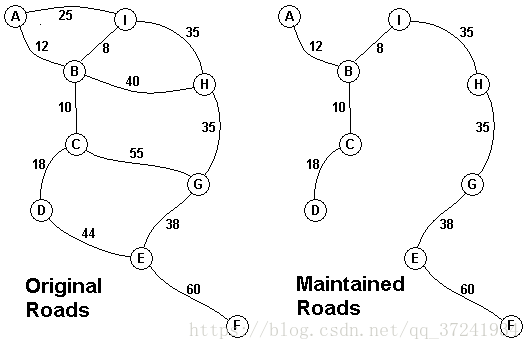

Problem Description

给你几个点，给出点与点之间的距离，求最小生成树。

Sample Input

A 2 B 12 I 25

B 3 C 10 H 40 I 8

C 2 D 18 G 55

D 1 E 44

E 2 F 60 G 38

F 0

G 1 H 35

H 1 I 35

A 2 B 10 C 40

B 1

C 20

Sample Output

216

这是一道最小生成树·算法题，最小生成树有两种方法：一是prim算法 https://mp.youkuaiyun.com/postedit/81133651，二是Kruskal算法。

也可以做做大量图论题：https://mp.youkuaiyun.com/postedit/81161939

#include<iostream>
#include<stdio.h>
using namespace std;
#define MAX 100
#define MAXCOST 0x7fffffff
int graph[MAX][MAX];
int prim(int graph[][MAX], int n)
{
	int lowcost[MAX];//i-max的距离 	
	int mst[MAX];//表示i的起点是谁 	
	int i, j, min, minid, sum = 0;
	for (i = 2; i <= n; i++)	
	{	
		lowcost[i] = graph[1][i];	
		mst[i] = 1;
	}//默认起点是1 	
	mst[1] = 0;
	for (i = 2; i <= n; i++)	
	{
	min = MAXCOST;	
	minid = 0;	
		for (j = 2; j <= n; j++)	
		{	
				if (lowcost[j] < min && lowcost[j] != 0)		
				{		
				min = lowcost[j];	
				minid = j;
				}
		}//找出距离1最近的点 
	sum += min;
	lowcost[minid] = 0;
		for (j = 2; j <= n; j++)	
		{
			if (graph[minid][j] < lowcost[j])	
			{
				lowcost[j] = graph[minid][j];	
				mst[j] = minid;
			}
		}//相当于利用mind作为新的起点来更新lowcost[]; 
	}
	return sum;
}
int main()
{
	int i, j, k, m, n,t,l;
	char s;
	int x, y, cost;
	while(~scanf("%d",&m)&&m){//m=顶点的个数，n=边的个
	//初始化图G
	for (i = 1; i <= m; i++)
	{
		for (j = 1; j <= m; j++)	
		{
			graph[i][j] = MAXCOST;
		}
	}
	//构建图G
	for (k = 1; k <m; k++)	
	{
		getchar();
		scanf("%c %d",&s,&t);
		l=(s-'A')+1;
		if(t>0)
		{
			for(i=0;i<t;i++)	
			{
				getchar();
				scanf("%c %d",&s,&cost);
				j=(s-'A')+1;
				graph[l][j] = cost;
				graph[j][l] = cost;
			}
		}
	}	
	cost = prim(graph, m);
	cout << cost << endl;
	}
	return 0;
}