numpy——用余弦相似度和SVD分解分别求解文档相似度

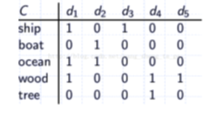
用余弦相似度和SVD分解分别计算各（d2,d3）文档的相似度，并比较两种方法得出结果的合理性。

                                                                  

 

import numpy as np

d1 = np.array([[1, 0, 1, 1, 0]])
d2 = np.array([[0, 1, 1, 0, 0]])
d3 = np.array([[1, 0, 0, 0, 0]])
d4 = np.array([[0, 0, 0, 1, 1]])
d5 = np.array([[0, 0, 0, 1, 0]])
num = float(d2.dot(d3.T))
denom = np.linalg.norm(d2) * np.linalg.norm(d3)
cos = num / denom  # 余弦值
sim = 0.5 + 0.5 * cos  # 根据皮尔逊相关系数归一化
print("余弦相似度为：", sim)

C = np.vstack((d1, d2, d3, d4, d5)).T
U, sigma, VT = np.linalg.svd(C)
# 按照前k个奇异值的平方和占总奇异值的平方和的百分比来确定k的值,后续计算SVD时需要将原始矩阵转换到k维空间
percentag