2高精度 1474. 多项式 A + B PAT甲级真题1002
1474. 多项式 A + B
给定两个多项式 A 和 B,计算 A+B 的结果。
输入格式
共两行,每行包含一个多项式的信息,格式如下:
K N1 aN1 N2 aN2 … NK aNK
其中,K 表示多项式中非零项的数量,Ni和 aNi 分别表示其中一个非零项的指数和系数。
输出格式
按照与输入相同的格式,输出 A+B的结果。
结果中的各项的系数均保留一位小数。
数据范围
K为整数,1≤K≤10。
Ni为整数,0≤NK < ⋯ < N2 < N1≤1000。
aNi为浮点数,−100≤aNi≤100。
输入样例:
2 1 2.4 0 3.2
2 2 1.5 1 0.5
输出样例:
3 2 1.5 1 2.9 0 3.2
This time, you are supposed to find A+B where A and B are two polynomials.
Input
Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial: K N1 aN1 N2 aN2 … NK aNK, where K is the number of nonzero terms in the polynomial, Ni and aNi (i=1, 2, …, K) are the exponents and coefficients, respectively. It is given that 1 <= K <= 10,0 <= NK < … < N2 < N1 <=1000.
Output
For each test case you should output the sum of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate to 1 decimal place.
Sample Input
2 1 2.4 0 3.2
2 2 1.5 1 0.5
Sample Output
3 2 1.5 1 2.9 0 3.2
题目大意:计算多项式A+B的和~
分析:设立c数组,长度为指数的最大值,c[i] = j表示指数i的系数为j,接收a和b输入的同时将对应指数的系数加入到c中,累计c中所有非零系数的个数,然后从前往后输出所有系数不为0的指数和系数~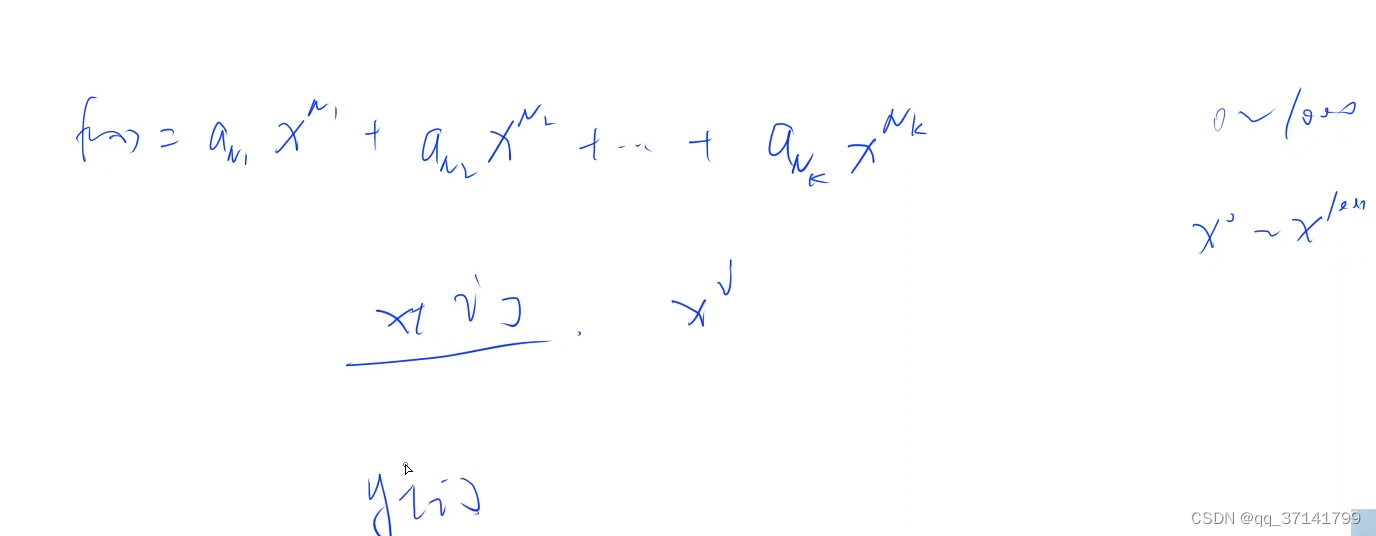
//1474. 多项式 A + B
//
//给定两个多项式 A和 B,计算 A + B的结果。
//
//输入格式
//共两行,每行包含一个多项式的信息,格式如下:
//
//K N1 aN1 N2 aN2 … NK aNK
//其中,K表示多项式中非零项的数量,Ni和 aNi分别表示其中一个非零项的 指数 和 系数。
//
//输出格式
//按照与输入相同的格式,输出 A + B的结果。
//
//结果中的各项的系数均保留一位小数。
//
//数据范围
//K为整数,1≤K≤10。
//Ni为整数,0≤NK < ⋯ < N2 < N1≤1000。
//aNi为浮点数,−100≤aNi≤100。
//
//输入样例:
//2 1 2.4 0 3.2
//2 2 1.5 1 0.5
//输出样例:
//3 2 1.5 1 2.9 0 3.2
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<map>
#include <unordered_set>
#include <set>
#include <unordered_map>
#include<algorithm>
#include<deque>
#include <math.h>
#include<cstdio>
using namespace std;
const int N = 1010;
double a[N];//存放第一个数,的幂次和系数
double b[N];//存放第二个数,的幂次和系数
double c[N];
class Solution {
public:
void func() {
int k;//第一个多项式有k项(系数^幂次是一项)
cin >> k;
while (k--) // 读入第一个多项式
{
int n;//幂次
double v;//系数
cin >> n >> v;
a[n] = v;//幂次是n,系数是v
}
cin >> k;
while (k--) // 读入第二个多项式
{
int n;
double v;
cin >> n >> v;
b[n] = v;
}
//a[i]就是系数i的幂次,b[i]就是也是系数i的幂次
//就是幂次相加,放进c[i]中,最后i的幂次是c[i] = a[i] + b[i];
for (int i = 0; i < N; i++) {
c[i] = a[i] + b[i];
}
k = 0;//记录求和之后的多项式c[]一共有几项
for (int i = 0; i < N; i++)
if (c[i])
k++;
cout << k;
for (int i = N - 1; i >= 0; i--)
if (c[i])
printf(" %d %.1lf", i, c[i]);//先输出幂次,再输出系数
}
};
class Solution2 {
public:
void func() {
}
};
int main() {
Solution s;
s.func();
return 0;
}
2高精度2 1481. 多项式乘积 PAT甲级真题1009
1481. 多项式乘积
给定两个多项式 A 和 B,计算 A×B的结果。
输入格式
共两行,每行包含一个多项式的信息,格式如下:
K N1 aN1 N2 aN2 … NK aNK
其中,K 表示多项式中非零项的数量,Ni和 aNi 分别表示其中一个非零项的指数和系数。
输出格式
按照与输入相同的格式,输出 A×B 的结果。
结果中的各项的系数均保留一位小数。
数据范围
K为整数,1≤K≤10。
Ni为整数,0≤NK < ⋯ < N2 < N1≤1000。
aNi为浮点数,−100≤aNi≤100。
输入样例:
2 1 2.4 0 3.2
2 2 1.5 1 0.5
输出样例:
3 3 3.6 2 6.0 1 1.6
This time, you are supposed to find A*B where A and B are two polynomials.
Input Specification:
Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial: K N1 aN1 N2 aN2 … NK aNK, where K is the number of nonzero terms in the polynomial, Ni and aNi (i=1, 2, …, K) are the exponents and coefficients, respectively. It is given that 1 <= K <= 10, 0 <= NK < … < N2 < N1 <=1000.
Output Specification:
For each test case you should output the product of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate up to 1 decimal place.
Sample Input
2 1 2.4 0 3.2
2 2 1.5 1 0.5
Sample Output
3 3 3.6 2 6.0 1 1.6
分析:简单模拟~double类型的arr数组保存第一组数据,ans数组保存结果。当输入第二组数据的时候,一边进行运算一边保存结果。最后按照指数递减的顺序输出所有不为0的项~
注意:因为相乘后指数可能最大为2000,所以ans数组最大要开到2001~
//1481. 多项式乘积
//
//给定两个多项式 A和 B,计算 A×B的结果。
//
//输入格式
//共两行,每行包含一个多项式的信息,格式如下:
//
//K N1 aN1 N2 aN2 … NK aNK
//其中,K表示多项式中非零项的数量,Ni和 aNi分别表示其中一个非零项的指数和系数。
//
//输出格式
//按照与输入相同的格式,输出 A×B的结果。
//
//结果中的各项的系数均保留一位小数。
//
//数据范围
//K为整数,1≤K≤10。
//Ni为整数,0≤NK < ⋯ < N2 < N1≤1000。
//aNi为浮点数,−100≤aNi≤100。
//
//输入样例:
//2 1 2.4 0 3.2
//2 2 1.5 1 0.5
//输出样例:
//3 3 3.6 2 6.0 1 1.6
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<map>
#include <unordered_set>
#include <set>
#include <unordered_map>
#include<algorithm>
#include<deque>
#include <math.h>
#include<cstdio>
using namespace std;
const int N = 1010;
/// <summary>
/// (3x^2+2x^3)∗(x^2+x)=3x^3+5x^4+2x^5
///
/// 1、开一个c[]数组,c[i]存储的是 指数是i 系数是c[i]
/// 2、将A多项式的指数和系数存在a[]数组中,B多项式的指数和系数存在b[]数组中
/// 3、将A多项式与B多项式的每一项进行相乘,系数相乘,指数相加,
/// 即将a[]数组中每个元素与b[]数组中的每个元素进行相乘,
/// 结果存在c[]中,即c[i + j] += a[i] * b[j]
/// i+j是幂次,c[i + j] += a[i] * b[j]是系数
/// 4、将c[]数组中存的指数和系数从大到小输出
/// </summary>
//c=a*b,a有n位,b有n位,c可能有2n位,所以大小开到N*2
double a[N], b[N], c[N * 2];
class Solution {
public:
void input(double a[]){
int k;
cin >> k;
while (k--) {
int n;
double v;
cin >> n >> v;
a[n] = v;//幂次是n,系数是v
}
}
void func() {
input(a);
input(b);
// 做乘法
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
c[i + j] += b[i] * a[j];
}
}
//K表示多项式中非零项的数量
int k = 0;
for (int i = 0; i < N * 2; i++) {
if (c[i]) {
k++;
}
}
cout << k;
for (int i = N * 2 - 1; i >= 0; i--) {
if (c[i]) {
//结果中的各项的系数均保留一位小数。
printf(" %d %.1lf", i, c[i]);
}
}
}
};
class Solution2 {
public:
void func() {
}
};
int main() {
Solution s;
s.func();
return 0;
}
2高精度3 1500. 趣味数字 PAT甲级真题1023
1500. 趣味数字
请注意,数字 123456789是一个 9位数字,完全由 1到 9组成,没有重复。
将其加倍,我们将获得 246913578,它恰好是另一个 9位数字,恰好由 1到 9组成,只是排列不同。
现在,给定你一个 k位的数字,请你判断将其加倍以后得到的数字是否可以由原数字的各数位重新排列得到。
输入格式
共一行,包含一个整数。
输出格式
输出共两行
如果原数字的各数位重新排列可以得到加倍后的数字,则在第一行输出 Yes,否则输出 No。
第二行,输出加倍后得到的数字。
数据范围
输入数字不超过 20位。
输入样例:
1234567899
输出样例:
Yes
2469135798
Notice that the number 123456789 is a 9-digit number consisting exactly the numbers from 1 to 9, with no duplication. Double it we will obtain 246913578, which happens to be another 9-digit number consisting exactly the numbers from 1 to 9, only in a different permutation. Check to see the result if we double it again!
Now you are suppose to check if there are more numbers with this property. That is, double a given number with k digits, you are to tell if the resulting number consists of only a permutation of the digits in the original number.
Input Specification:
Each input file contains one test case. Each case contains one positive integer with no more than 20 digits.
Output Specification:
For each test case, first print in a line "Yes" if doubling the input number gives a number that consists of only a permutation of the digits in the original number, or "No" if not. Then in the next line, print the doubled number.
Sample Input:
1234567899
Sample Output:
Yes
2469135798
题目大意:给出一个长度不超过20的整数,问这个整数两倍后的数位是否为原数位的一个排列。不管是yes还是no最后都要输出整数乘以2的结果
分析:使用char数组存储这个数,没个数的数位乘以2 + 进位,同时设立book来标记数位出现的情况。只有最后book的每个元素都是0的时候才说明这两个数字是相等的一个排列结果~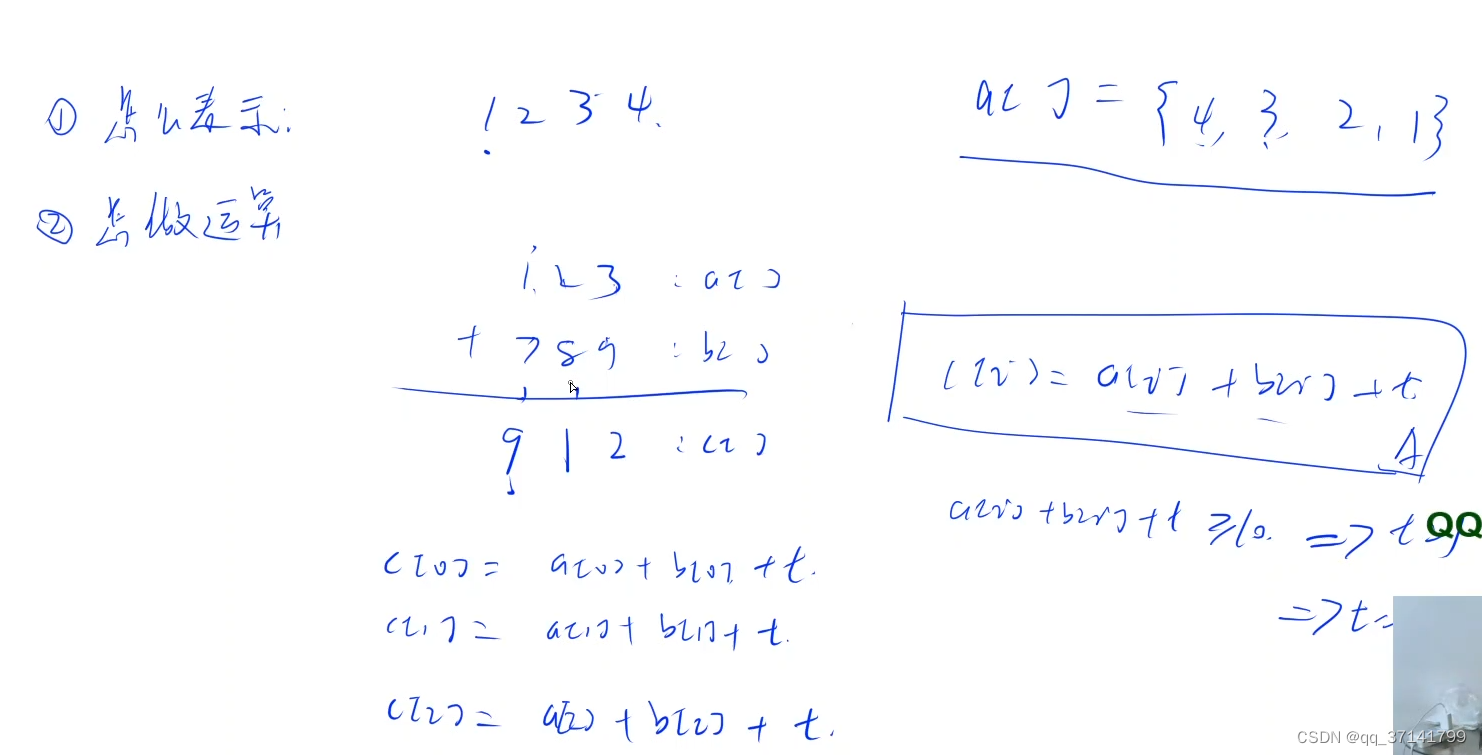
//1500. 趣味数字
//
//请注意,数字 123456789是一个 9位数字,完全由 1到 9组成,没有重复。
//
//将其加倍,我们将获得 246913578,它恰好是另一个 9位数字,恰好由 1到 9组成,只是排列不同。
//
//现在,给定你一个 k位的数字,请你判断将其加倍以后得到的数字是否可以由原数字的各数位重新排列得到。
//
//输入格式
//共一行,包含一个整数。
//
//输出格式
//输出共两行
//
//如果原数字的各数位重新排列可以得到加倍后的数字,则在第一行输出 Yes,否则输出 No。
//
//第二行,输出加倍后得到的数字。
//
//数据范围
//输入数字不超过 20位。
//
//输入样例:
//1234567899
//输出样例:
//Yes
//2469135798
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<map>
#include <unordered_set>
#include <set>
#include <unordered_map>
#include<algorithm>
#include<deque>
#include <math.h>
#include<cstdio>
using namespace std;
class Solution {
public:
void func() {
string A;//输入567
vector<int> a;//将字符串A存到该vector里
cin >> A;
//倒着放,后面加法的时候从下标0开始取,相当于原来的数字最末尾开始相加
//vector<int> a里面是765
for (int i = A.size() - 1; i >= 0; i--) {
a.push_back(A[i] - '0');//将字符数字转换成整形,
}
//i=0时,a[0]=7,s=7+7+0=14,s % 10=4,b.push_back(4),t=s/10=1
//i=1时,a[1]=6,s=6+6+1=13,s%10=3,b.push_back(3),t=s/10=1;
//i=2时,a[2]=5,s=5+5+1=11,s%10=1,b.push_back(1),t=s/10=1;
//if(t!=0){b.push_back(1)}
vector<int> b;
int t = 0;
for (int i = 0; i < a.size(); i++){
int s = a[i] + a[i] + t;
b.push_back(s % 10);
t = s / 10;
}
if (t!=0) b.push_back(t);
vector<int> c = b;
//竟然sort 之后去比较
sort(a.begin(), a.end());
sort(c.begin(), c.end());
if (a == c) puts("Yes");
else puts("No");
for (int i = b.size() - 1; i >= 0; i--) cout << b[i];
}
};
class Solution2 {
public:
void func() {
}
};
int main() {
Solution s;
s.func();
return 0;
}
2高精度4 1501. 回文数 PAT甲级真题1024
1501. 回文数
如果一个数字从前往后读和从后往前读都一样,那么这个数字就是回文数字。
所有一位数字都是回文数字。
非回文数字可以通过一系列的操作与回文数字配对。
首先,将非回文数字反转,让反转后的数字与原数字相加,得到一个新的数字。
如果新的数字不是回文数字,那么就重复此操作,直到得到回文数字为止。
例如,我们从 67开始,经过两次操作可以得到一个回文数字:67 + 76 = 143,143 + 341 = 484。
对于给定的任意正整数 N,请你找到它的配对回文数并输出得到该回文数需要的操作次数。
输入格式
共一行,包含两个整数 N和 K,分别表示给定整数以及最大操作次数。
输出格式
共两行,第一行输出配对回文数。
第二行输出得到配对回文数所需要的操作次数。
如果经过 K次操作后,仍然无法得到回文数字。
那么,第一行输出 K次操作后得到的数字。
第二行输出 K。
数据范围
1≤N≤10^10
1≤K≤100
输入样例1:
67 3
输出样例1:
484
2
输入样例2:
69 3
输出样例2:
1353
3
A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are palindromic numbers.
Non-palindromic numbers can be paired with palindromic ones via a series of operations. First, the non-palindromic number is reversed and the result is added to the original number. If the result is not a palindromic number, this is repeated until it gives a palindromic number. For example, if we start from 67, we can obtain a palindromic number in 2 steps: 67 + 76 = 143, and 143 + 341 = 484.
Given any positive integer N, you are supposed to find its paired palindromic number and the number of steps taken to find it.
Input Specification:
Each input file contains one test case. Each case consists of two positive numbers N and K, where N (<= 10^10) is the initial numer and K (<= 100) is the maximum number of steps. The numbers are separated by a space.
Output Specification:
For each test case, output two numbers, one in each line. The first number is the paired palindromic number of N, and the second number is the number of steps taken to find the palindromic number. If the palindromic number is not found after K steps, just output the number obtained at the Kth step and K instead.
Sample Input 1:
67 3
Sample Output 1:
484
2
Sample Input 2:
69 3
Sample Output 2:
1353
3
题目大意:给定一个数字,和允许翻转后相加的次数cnt,求要多少次才能变成一个回文数字,输出那个回文数字和翻转相加了多少次,如果本身就是回文数字就输出0次,如果超过给定的次数cnt了,就输出那个不是回文的结果,并且输出给定的次数cnt
分析:1、会超出long int类型(会有两个点溢出错误),所以用字符串存储,大整数相加
2、可以通过对字符串翻转后比较来判断是否为回文串
//1501. 回文数
//
//如果一个数字从前往后读和从后往前读都一样,那么这个数字就是回文数字。
//所有一位数字都是回文数字。
//非回文数字可以通过一系列的操作与回文数字配对。
//
//首先,将非回文数字反转,让反转后的数字与原数字相加,得到一个新的数字。
//如果新的数字不是回文数字,那么就重复此操作,直到得到回文数字为止。
//例如,我们从 67开始,经过两次操作可以得到一个回文数字:67 + 76 = 143,143 + 341 = 484。
//对于给定的任意正整数 N,请你找到它的配对回文数并输出得到该回文数需要的操作次数。
//
//输入格式
//共一行,包含两个整数 N和 K,分别表示给定整数以及最大操作次数。
//
//输出格式
//共两行,第一行输出配对回文数。
//第二行输出得到配对回文数所需要的操作次数。
//
//如果经过 K次操作后,仍然无法得到回文数字。
//那么,第一行输出 K次操作后得到的数字。
//第二行输出 K。
//
//数据范围
//1≤N≤10^10
//1≤K≤100
//输入样例1:
//67 3
//输出样例1:
//484
//2
//
//输入样例2:
//69 3
//输出样例2:
//1353
//3
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<map>
#include <unordered_set>
#include <set>
#include <unordered_map>
#include<algorithm>
#include<deque>
#include <math.h>
#include<cstdio>
using namespace std;
class Solution {
public:
//判断是否是回文数
//两头指针往中间走
bool check(vector<int>& num) {//用引用,不会重新创建vector,代码会快
for (int i = 0, j = num.size() - 1; i < j; i++, j--)
if (num[i] != num[j])
return false;
return true;
}
//高精度加法
vector<int> add(vector<int>& a, vector<int>& b) {
vector<int> c;
//i < a.size() || i < b.size() || t 是a没循环完或者b没循环完或者t(进位)!=0
//三者都不成立才会结束循环
for (int i = 0, t = 0; i < a.size() || i < b.size() || t; i++) {
int s = t;
if (i < a.size()) s += a[i];
if (i < b.size()) s += b[i];
c.push_back(s % 10);
t = s / 10;
}
return c;
}
void func() {
string n;
int k;
cin >> n >> k;
vector<int> a;
for (int i = n.size() - 1; i >= 0; i--) a.push_back(n[i] - '0');
int cnt = 0;//记录回文数循环了几次
if (!check(a)) {
while (cnt < k) {
//将vector<int> a 倒着赋值给vector<int> b
vector<int> b(a.rbegin(), a.rend());
a = add(a, b);
cnt++;
if (check(a)) break;
}
}
//共两行,第一行输出配对回文数。
//第二行输出得到配对回文数所需要的操作次数。
//倒序输出
for (int i = a.size() - 1; i >= 0; i--) cout << a[i];
//输出换行和得到配对回文数所需要的操作次数
cout << endl << cnt << endl;
}
};
class Solution2 {
public:
void func() {
}
};
int main() {
Solution s;
s.func();
return 0;
}
2高精度5 1544. 霍格沃茨的 A + B PAT甲级真题1058
1544. 霍格沃茨的 A + B
如果你是哈利波特的粉丝,你就会知道魔术世界有其自己的货币体系。
正如海格对哈利解释的那样:“17 个银镰刀(Sickle)可以换 1 个帆船(Galleon),29 个克努特(Knut)可以换 1 个银镰刀。”
你的工作是编写一个计算 A+B 的程序,其中 A 和 B 以 Galleon.Sickle.Knut 的标准形式给出(Galleon 是一个范围在 [0,107] 的整数,Sickle 是一个范围在 [0,17) 的整数,Knut 是一个范围在 [0,29) 的整数)。
输入格式
共一行,包含 A 和 B,格式如题目所述。
输出格式
按照题目所述标准格式,输出 A+B 的结果。
输入样例:
3.2.1 10.16.27
输出样例:
14.1.28
If you are a fan of Harry Potter, you would know the world of magic has its own currency system — as Hagrid explained it to Harry, “Seventeen silver Sickles to a Galleon and twenty-nine Knuts to a Sickle, it’s easy enough.” Your job is to write a program to compute A+B where A and B are given in the standard form of “Galleon.Sickle.Knut” (Galleon is an integer in [0, 107], Sickle is an integer in [0, 17), and Knut is an integer in [0, 29)).
Input Specification:
Each input file contains one test case which occupies a line with A and B in the standard form, separated by one space.
Output Specification:
For each test case you should output the sum of A and B in one line, with the same format as the input.
Sample Input:
3.2.1 10.16.27
Sample Output:
14.1.28
题目大意:17个Sickle对换一个Galleon,29个Knut对换一个Sickle。根据Galleon.Sickle.Knut的方式相加A和B
分析:像相加算术一样从后往前按位相加,处理好进位~
//1544. 霍格沃茨的 A + B
//
//如果你是哈利波特的粉丝,你就会知道魔术世界有其自己的货币体系。
//
//正如海格对哈利解释的那样:“17个银镰刀(Sickle)可以换 1个帆船(Galleon),
//29个克努特(Knut)可以换 1个银镰刀。”
//
//你的工作是编写一个计算 A + B的程序,
//其中 A和 B以 Galleon.Sickle.Knut 的标准形式给出
//(Galleon 是一个范围在[0, 107]的整数,Sickle 是一个范围在[0, 17)的整数,
//Knut 是一个范围在[0, 29)的整数)。
//
//输入格式
//共一行,包含 A和 B,格式如题目所述。
//
//输出格式
//按照题目所述标准格式,输出 A + B的结果。
//
//输入样例:
//3.2.1 10.16.27
//输出样例:
//14.1.28
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<map>
#include <unordered_set>
#include <set>
#include <unordered_map>
#include<algorithm>
#include<deque>
#include <math.h>
#include<cstdio>
using namespace std;
class Solution {
public:
void func() {
int a, b, c, d, e, f;
scanf("%d.%d.%d %d.%d.%d", &a, &b, &c, &d, &e, &f);
a += d, b += e, c += f;
b += c / 29, c %= 29;
a += b / 17, b %= 17;
printf("%d.%d.%d\n", a, b, c);
}
};
class Solution2 {
public:
void func() {
}
};
int main() {
Solution s;
s.func();
return 0;
}
2高精度6 1629. 延迟的回文数 PAT甲级真题1136
1629. 延迟的回文数
给定一个 k + 1位的正整数 N,写成 ak⋯a1a0的形式,其中对所有 i有 0≤ai < 10且 ak大于 0。
N被称为一个回文数,当且仅当对所有 i有 ai = ak−i。
零也被定义为一个回文数。
非回文数也可以通过一系列操作变出回文数。
首先将该数字逆转,再将逆转数与该数相加,如果和还不是一个回文数,
就重复这个逆转再相加的操作,直到一个回文数出现。
如果一个非回文数可以变出回文数,就称这个数为延迟的回文数。
给定任意一个正整数,本题要求你找到其变出的那个回文数。
输入格式
输入在一行中给出一个不超过 1000位的正整数。
输出格式
对给定的整数,一行一行输出其变出回文数的过程。
每行格式如下:
A + B = C
其中 A 是原始的数字,B 是 A 的逆转数,C 是它们的和。A 从输入的整数开始。
重复操作直到 C 在 10步以内变成回文数,这时在一行中输出 C is a palindromic number.;
或者如果 10步都没能得到回文数,最后就在一行中输出 Not found in 10 iterations.。
输入样例1:
97152
输出样例1:
97152 + 25179 = 122331
122331 + 133221 = 255552
255552 is a palindromic number.
输入样例2:
196
输出样例2:
196 + 691 = 887
887 + 788 = 1675
1675 + 5761 = 7436
7436 + 6347 = 13783
13783 + 38731 = 52514
52514 + 41525 = 94039
94039 + 93049 = 187088
187088 + 880781 = 1067869
1067869 + 9687601 = 10755470
10755470 + 07455701 = 18211171
Not found in 10 iterations.
Consider a positive integer N written in standard notation with k+1 digits ai as ak…a1a0 with 0 <= ai < 10 for all i and ak > 0. Then N is palindromic if and only if ai = ak-i for all i. Zero is written 0 and is also palindromic by definition.
Non-palindromic numbers can be paired with palindromic ones via a series of operations. First, the non-palindromic number is reversed and the result is added to the original number. If the result is not a palindromic number, this is repeated until it gives a palindromic number. Such number is called a delayed palindrome. (Quoted from https://en.wikipedia.org/wiki/Palindromic_number)
Given any positive integer, you are supposed to find its paired palindromic number.
Input Specification:
Each input file contains one test case which gives a positive integer no more than 1000 digits.
Output Specification:
For each test case, print line by line the process of finding the palindromic number. The format of each line is the following:
A + B = C
where A is the original number, B is the reversed A, and C is their sum. A starts being the input number, and this process ends until C becomes a palindromic number — in this case we print in the last line “C is a palindromic number.”; or if a palindromic number cannot be found in 10 iterations, print “Not found in 10 iterations.” instead.
Sample Input 1:
97152
Sample Output 1:
97152 + 25179 = 122331
122331 + 133221 = 255552
255552 is a palindromic number.
Sample Input 2:
196
Sample Output 2:
196 + 691 = 887
887 + 788 = 1675
1675 + 5761 = 7436
7436 + 6347 = 13783
13783 + 38731 = 52514
52514 + 41525 = 94039
94039 + 93049 = 187088
187088 + 880781 = 1067869
1067869 + 9687601 = 10755470
10755470 + 07455701 = 18211171
Not found in 10 iterations.
分析:1 将字符串倒置与原字符串比较看是否相等可知s是否为回文串
2 字符串s和它的倒置t相加,只需从头到尾相加然后再倒置(记得要处理最后一个进位carry,如果有进位要在末尾+’1’)
3 倒置可采用algorithm头文件里面的函数reverse(s.begin(), s.end())直接对s进行倒置
//1629. 延迟的回文数
//
//给定一个 k + 1位的正整数 N,写成 ak⋯a1a0的形式,其中对所有 i有 0≤ai < 10且 ak大于 0。
//
//N被称为一个回文数,当且仅当对所有 i有 ai = ak−i。
//
//零也被定义为一个回文数。
//
//非回文数也可以通过一系列操作变出回文数。
//
//首先将该数字逆转,再将逆转数与该数相加,如果和还不是一个回文数,
//就重复这个逆转再相加的操作,直到一个回文数出现。
//
//如果一个非回文数可以变出回文数,就称这个数为延迟的回文数。
//
//给定任意一个正整数,本题要求你找到其变出的那个回文数。
//
//输入格式
//输入在一行中给出一个不超过 1000位的正整数。
//
//输出格式
//对给定的整数,一行一行输出其变出回文数的过程。
//
//每行格式如下:
//
//A + B = C
//其中 A 是原始的数字,B 是 A 的逆转数,C 是它们的和。A 从输入的整数开始。
//
//重复操作直到 C 在 10步以内变成回文数,这时在一行中输出 C is a palindromic number.;
//
//或者如果 10步都没能得到回文数,最后就在一行中输出 Not found in 10 iterations.。
//
//输入样例1:
//97152
//输出样例1:
//97152 + 25179 = 122331
//122331 + 133221 = 255552
//255552 is a palindromic number.
//输入样例2:
//196
//输出样例2:
//196 + 691 = 887
//887 + 788 = 1675
//1675 + 5761 = 7436
//7436 + 6347 = 13783
//13783 + 38731 = 52514
//52514 + 41525 = 94039
//94039 + 93049 = 187088
//187088 + 880781 = 1067869
//1067869 + 9687601 = 10755470
//10755470 + 07455701 = 18211171
//Not found in 10 iterations.
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<map>
#include <unordered_set>
#include <set>
#include <unordered_map>
#include<algorithm>
#include<deque>
#include <math.h>
#include<cstdio>
using namespace std;
//yxc://比1501.回文数多了打印这几步而已
class Solution {
public:
bool check(vector<int> A){
for (int i = 0, j = A.size() - 1; i < j; i++, j--)
if (A[i] != A[j])
return false;
return true;
}
void print(vector<int> A){
for (int i = A.size() - 1; i >= 0; i--) cout << A[i];
}
vector<int> add(vector<int> A, vector<int> B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size() || i < B.size() || t; i++)
{
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
return C;
}
void func() {
string a;
cin >> a;
vector<int> A;
// //倒着放
for (int i = 0; i < a.size(); i++) A.push_back(a[a.size() - 1 - i] - '0');
for (int i = 0; i < 10; i++) {
if (check(A)) break;
vector<int> B(A.rbegin(), A.rend());
//比1501.回文数多了这几部而已
print(A), cout << " + ", print(B), cout << " = ";
A = add(A, B);
print(A), cout << endl;
}
if (check(A)) print(A), cout << " is a palindromic number." << endl;
else puts("Not found in 10 iterations.");
}
};
class Solution2 {
public:
void func() {
}
};
int main() {
Solution s;
s.func();
return 0;
}





















 308
308

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








