排序算法-快速排序之普通快排、双轴快排、三轴快排 另外关于挖坑实现快排的效率问题（java实现)

快速排序

基本思想

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另一部分的所有数据要小，然后再按此方法对着两部分数据分别快排。整个排序过程可以递归进行，以此达到数据变为有效序列。

假设要排序的数组为A[0],A[1].....A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比他小的数都放到它左边，所有比它大的数都放到它右边，这个过程就是一趟快速排序。快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束后产生变动。

一趟快速排序算法为：

1.设置两个变量i、j，排序开始时：i=0，j=arr.lenth-1

2.以第一个元素作为关键数据，赋值给key，即k=A[i]=A[0]

3.从j开始向前搜索，j--，直到找到第一个小于key的值A[j]，将A[j]和A[i]交换。

4.从i开始向后搜索，i++，直到找到第一个大于key的A[i]，将A[i]和A[j]交换。

5.重复步骤3、4直到i=j

关于快速排序的优化：

1.随机选取基准，因为在待排序列是部分有序时，固定选取基准使快排效率低下，要缓解这种情况，就引入了随机选取基点。使用随机数生成函数生成一个随机数rand，随机数的范围为[left,right]，并用此随机数为下标对应的元素a[rand]作为基点，并与第一个数交换。

优点：这是一种相对安全的策略，由于基点的位置是随机的，那么产生的分割也不会总是会出现劣质的分割。在整个数组数字完全相等时，仍然是最坏情况，时间复杂度是O(n²)。为什么是O(n²)？

如果是一个无序数组，[5,4,3,1,2]

第一次排序后：[2,1,3,4,5]

第二次排序：对[2,1]和[4,5]排序，[1,2,3,4,5]排序完成

如果有序呢？

设数组为1，2，3，4，5

第一次排序分为1和[2,3,4,5]

第二次排序后分为了[1,2]和[3,4,5]

第三次分为了[1,2,3]和[4,5]

第四次分为了[1,2,3,4]和[5]

排了n-1次，每次比较n次，所以是n²

2.三数中值分割法

一组序列的中值（中位数）是基点最好的选择（因为可以将序列平均分为两个子序列，但是计算一组数组的中位数比较耗时，会减慢快排的效率。但可以通过计算数组的第一个、中间位置、最后一个元素的中值来代替。使用三数分割法消除了预排序输入的坏情形。

3.在排序序列长度分割到一定大小后，使用插入排序。

优点：对于很小和部分有序的数组，快排效率不如插入排序。（但是经过我测试，在数据量小的时候只使用快排比使用快排+插入速度更快，在数据量很大时不管是<7还是<15的时候改成插入排序后，程序都运行不出来了）

4.在应对大量重复元素时，我们可以将数组切分为三部分，分别对应小于、等于、大于。

普通快排：

/**
 * 普通快排
 */

public class QuickSort2 {

    public static void main(String[] args) {

        int[] array = {6,1,100,32,22,2,6,321,25,99,54,33,11,54,23,1,5};

        quickSort(array,0,array.length-1);

        System.out.println(Arrays.toString(array));
    }

   

    //每次以第一个元素季即arr[l]为基准，比基准值小的在右，大的在左，
    //返回基准值最终在数组中的位置
    private static void quickSort(int[] arr, int l, int r) {
        if(l>=r)
            return;
        
        int v=arr[l];
        int j=l;
        //int temp=arr[l];
        for(int i=l+1;i<=r;i++) {
            //每次循环将小于v的往前换
            if(arr[i]<v) {
                int temp =arr[j+1];
                arr[j+1]=arr[i];
                arr[i]=temp;
                j++; //arr[j+1]始终是大于v的,arr[j]是最后一个<=v的

            }
        }
        //再将基准值移动到中间
        swap(arr,l,j);
        //最终j所指的位置就是中间值
        quickSort(arr, l, j-1);
        quickSort(arr, j+1, r);
    }

    
    private static void swap(int[] arr, int i, int j) {
        if(i!=j) {
            int temp =arr[j];
            arr[j]=arr[i];
            arr[i]=temp;
        }
    }
}

双路挖坑快排代码一：

public static void quick_sort(int s[],int l,int r){
        if(l<r){
            int i=adjustArray(s, l, r);
            quick_sort(s, l, i-1);
            quick_sort(s,i+1,r);
        }
    }
    public static int adjustArray(int s[],int l,int r){

        int i=l,j=r;
        //s[l]即s[i]就是第一个坑
        int x = s[l];

        while (i<j){
            //从右向左找小于x的数来填充s[l] 循环跳出即为找到
            while (i<j && s[j]>x)
                j--;
            if(i<j){
                s[i] = s[j];
                i++;
            }

            //从左向右找大于x的数来填充s[j]
            while (i<j && s[i]<x)
                i++;
            if(i<j){
                s[j] = s[i];
                j--;
            }
        }
        //退出时i=j,将x填到这个坑中
        s[i] = x;
        //返回调整后基准数的位置
        return i;
    }

上面代码不够简洁，对其进行组合整理后：

public static void quick_sort2(int[] s,int l,int r){
        if(l<r){
            //左边的起始位置，右边的起始位置，第一个数
            int i=l,j=r,x=s[l];
            while (i<j){
                while (i<j && s[j]>x)
                    j--;
                if(i<j){
                    s[i++] = s[j];
                }

                while (i<j && s[i]<x)
                    i++;
                if(i<j){
                    s[j--] = s[i];
                }
            }
            s[i] = x;
            quick_sort2(s,l,i-1);
            quick_sort2(s,i+1,r);
        }
    }

双路快排，经过测试比上面的挖坑快排速度更快：

/**
 * 双路快排写法2  较挖坑快排速度提升百分之三十左右
 */

public class QuickSort3 {

    public static void main(String[] args) {
        int[] array = ArrayUtil.bigArray();
        long time1 = System.currentTimeMillis();
        QuickSort(array,0,array.length-1);
        long time2 = System.currentTimeMillis();
        System.out.println(time2 - time1);
    }
        private static void QuickSort(int[] arr, int l, int r) {
            if(l>=r)
                return;

            swap(arr,l,(int)Math.random()*(r-l+1)+l);
            //满足arr[l+1,i)<=v,arr(j,r]>=v
            int v=arr[l];
            int i=l+1,j=r;
            while(true) {
                //从左到右扫描，扫描出第一个比base大的元素，然后i停在那里
                while(arr[i]<v&&i<r)//arr[i]不能=v，会导致v聚集在一边
                    i++;
                //从右到左扫描，扫描出第一个比base小的元素，然后j停在那里
                while(arr[j]>v&&j>l)
                    j--;
                if(i>=j)
                    break;
                swap(arr, i, j);
                i++;
                j--;
            }
            //将基准值交换到合适位置
             //因为j能遍历到0，而i只能从第1个往后找，如果第0个是最小的数，把会最小的数换到中间
            swap(arr, l, j);

            QuickSort(arr, l, j-1);
            QuickSort(arr, j+1, r);
        }
        private static void swap(int[] arr, int i, int j) {
            if(i!=j) {
                int temp=arr[i];
                arr[i]=arr[j];
                arr[j]=temp;
            }
        }
    }

三路快排：

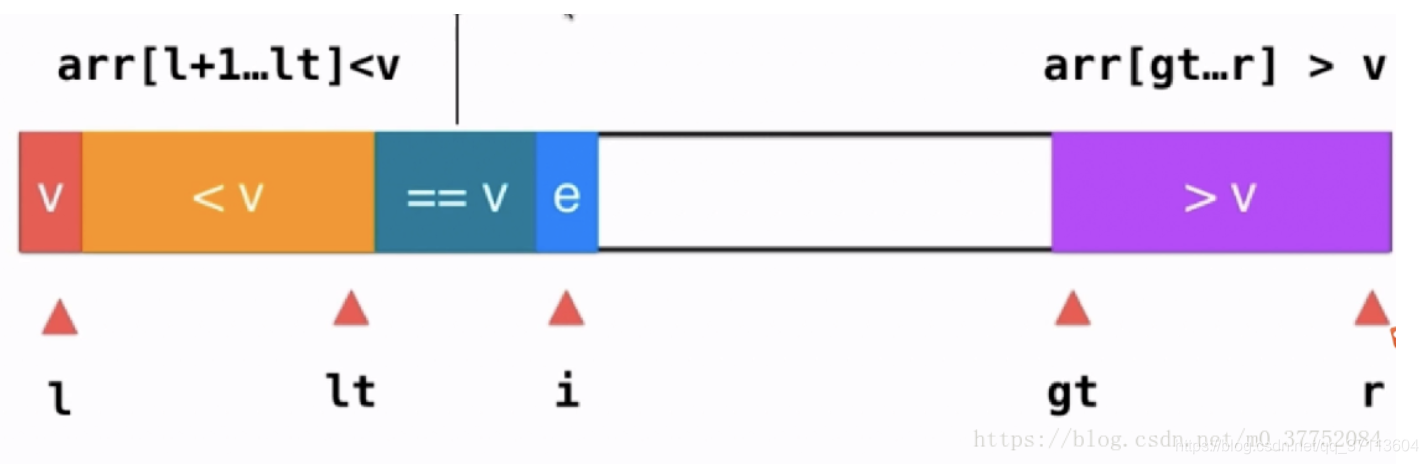
private static void quickSort3Ways(int[] arr,int left,int right){
        if (left >= right){
            return;
        }
        //基数
        int v = arr[left];
        //左边最接近v且等于v
        int lt = left;
        //右边最接近v且等于v
        int rt = right;
        //从第一个数开始比较
        int i=left+1;
        while (i<=rt){
            if(arr[i] < v){
                //把小的数往左放 如果第arr[1]<arr[0]  交换i和0上的数
                swap(arr,lt,i);
                i++;
                lt++;
            }else if (arr[i]>v){
                //大数放右边
                swap(arr,rt,i);
                rt--;
            }else{
                i++;
            }
        }
        //为什么这里是lt-1与rt+1 因为lt与rt索引指向的都是等于中间重复值的索引，中间的重复值已经是中值了
        quickSort3Ways(arr,left,lt-1);
        quickSort3Ways(arr,rt+1,right);
    }

 

为什么双路快排比挖坑快排更快？

测试数组：

72，6，57，88，60，42，83，73，48，85

双路快排：

第一趟将48和88交换，数组变为：72，6，57，48，60，42，83，73，88，85

第二趟i++到83才找到>72的数，j--到在42才找到小于72的数，这里选取i和j都行，与72交换。

这里就·暂且选取j吧，交换后变为：42，6，57，48，60，72，83，73，88，85

这样比72小的都到了左边，比72大的都到了右边

挖坑法：

第一趟排序：temp=72相当于在72挖了个坑，从后向前找j--，找到48小于72，将48放到72  arr[0]=arr[8]

48，6，57，88，60，42，83，73，48，85

然后从前向后找i++，找>48的数，找到88，将88放入48，arr[8]=arr[3]

48，6，57，88，60，42，83，73，88，85

第二趟排序：j--找到42，42放到88 arr[3]=arr[5]

48，6，57，42，60，42，83，73，88，85

break

arr[5]=72

最后排序结果：

48，6，57，42，60，72，83，73，88，85

从结果可以看出，42的位置较上面发生了变化。增加了排序的不稳定性。而且这种排序相当于使用数组中的元素作为了临时值去临时保存数组中别的数据，这种方法每次访问，交换，挖坑都要经过数组，在数组很大的情况下所耗费的资源比用临时值保存下数据，然后交换，耗费更多的时间与资源。

经过测试一千万条数据的排序：

挖坑快排：1321，1260，1299  大约稳定在1.3秒左右

双路快排：1067，1061，1032 大约稳定在1.0秒左右

一亿条数据：

挖坑快排：13004，12893，12996大约13秒左右

双路快排：10532，10807，10684大约10.5秒左右

三路快排：11038，10098，10571大约10秒吧，较双路快排慢了一点点。

一亿条数据当存在大量重复数据时：

挖坑：9405，10106大约9.7秒

双路：6464，6456大约6.5秒

三路：4173，4195大约4秒

三路(选取left为基数）：6729，6936大约7秒，可以看出存在大量重复数据时，还是随机选取基数速度更快

时空复杂度

快速排序的平均时间复杂度也是：O(nlogn)

最差是O(n²)即退换为冒泡排序时。最差的情况就是每一次取到的元素就是数组中最小/最大的，这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)

最优的情况下空间复杂度为：O(logn)  ；每一次都平分数组的情况

最差的情况下空间复杂度为：O( n )      ；退化为冒泡排序的情况