LeetCode：589. N叉树的前序遍历

589. N叉树的前序遍历

给定一个 N 叉树，返回其节点值的前序遍历。

例如，给定一个 3叉树 :

                  1

               /   |    \

           3      2      4

         /   \

       5      6

返回其前序遍历: [1,3,5,6,2,4]。

 

说明: 递归法很简单，你可以使用迭代法完成此题吗?

链接：https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal

参考：LeetCode题解

方法1 递归：

思路：跟二叉树的前序遍历相似，注意vector容器v要定义为全局v

时间复杂度：O(n) ?

空间复杂度： O(n) ?

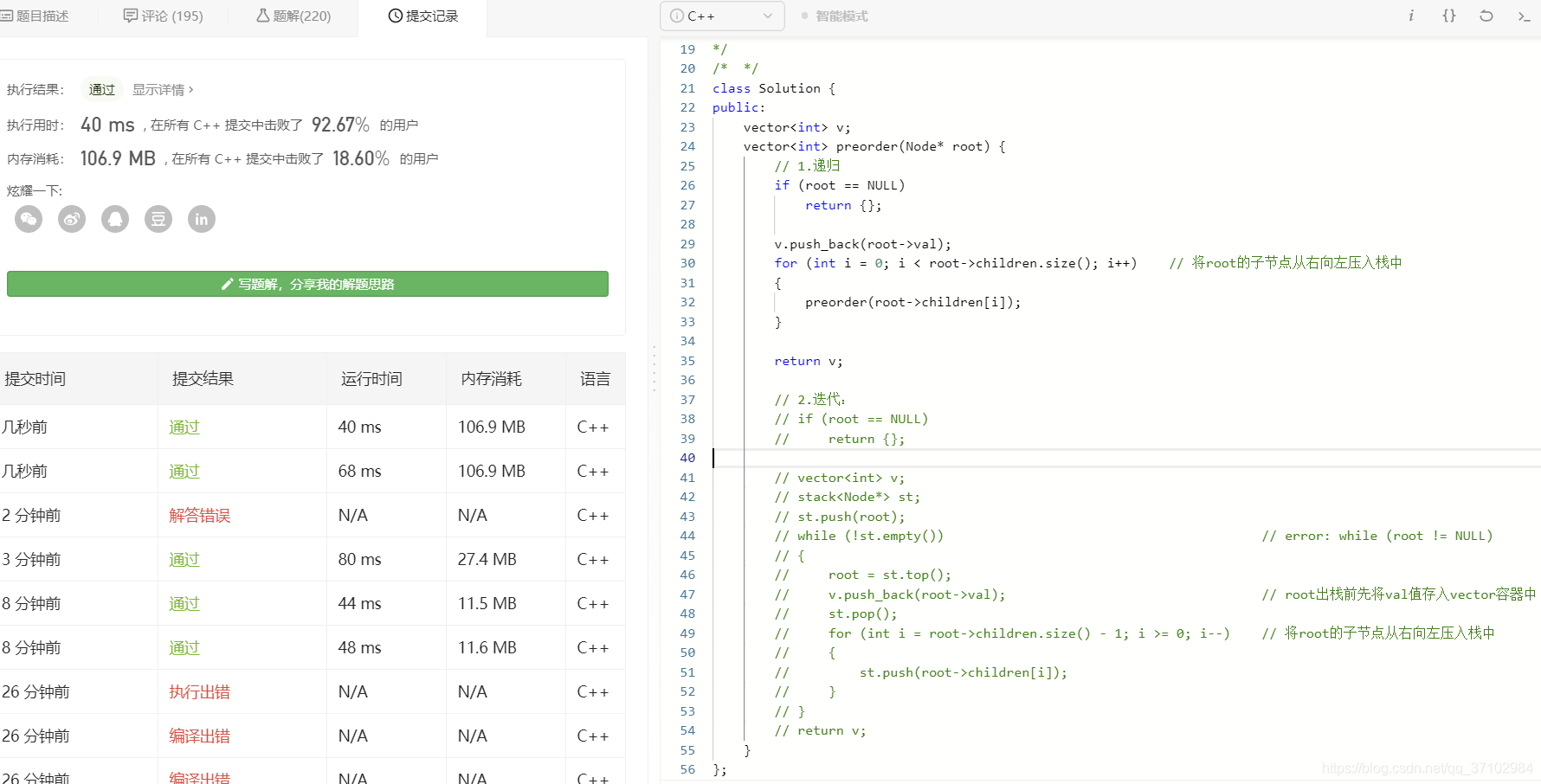
// 1. 递归
vector<int> v;                                          // 函数外定义全局vector容器v !!!
vector<int> preorder(Node* root) {
    if (root == NULL)
        return {};
    
    v.push_back(root->val);
    for (int i = 0; i < root->children.size(); i++)     // 将root的子节点从右向左压入栈中
    {
        preorder(root->children[i]);
    }
    
    return v;
}

 

方法2 迭代：

思路：

在将children压入栈中时，要注意顺序，从右往左压入栈中（而递归法会自动从最左边的children开始遍历）

另外，while条件是 while(!st.empty()) 栈非空！而不是常规二叉树的 while(root != NULL || !st.empty())

时间复杂度：O(n)，其中 n 是 N 叉树中的节点个数。每个节点只会入栈和出栈各一次。

空间复杂度：O(n)，在最坏的情况下，这棵 N 叉树只有 2 层，所有第 2 层的节点都是根节点的孩子。将根节点推出栈后，需要将这些节点都放入栈，共有 n-1 个节点，因此栈的大小为 O(n)

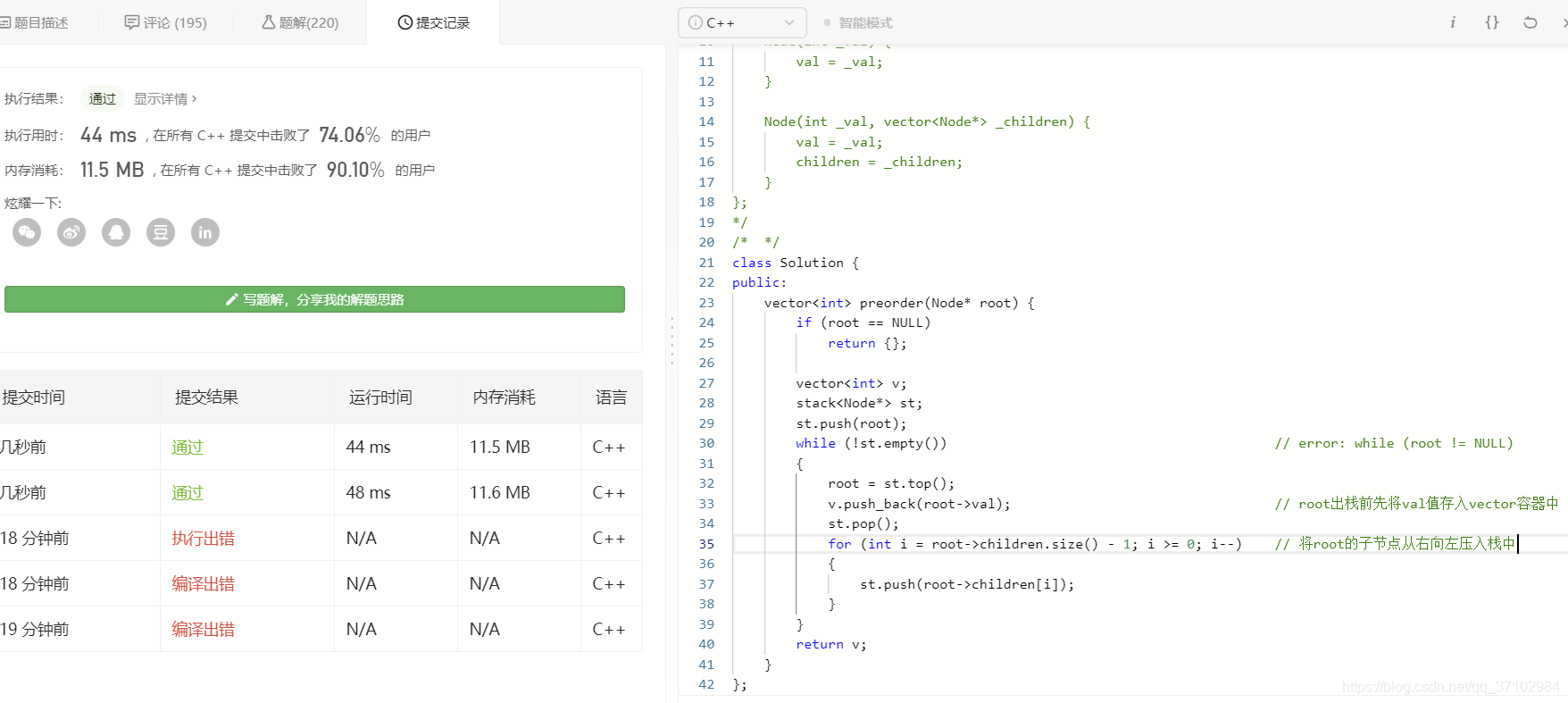
// 2. 迭代
vector<int> preorder(Node* root) {
   if (root == NULL) 
        return {};

    vector<int> v;
    stack<Node*> st;
    st.push(root);                                              // 先将根节点值入栈
    while (!st.empty())                                         // 注意条件：栈非空！error: while (root != NULL)
    {
        root = st.top();
        v.push_back(root->val);                                 // root出栈前先将val值存入vector容器中
        st.pop();
        for (int i = root->children.size() - 1; i >= 0; i--)    // 将root的子节点从右向左入栈，最左边后入栈，所以能先出栈获取到
        {
            st.push(root->children[i]);                         // 将root的子节点按顺序分别入栈
        }
    }
    return v;
}