19.二叉树采用顺序存储方式保存,结点X保存在数组A[7]中,若X有右孩子结点Y,则Y保存在_________________中。
【答案】A[16]
【解析】二叉树性质五修改为:如果将一棵有n个结点的完全二叉树按层从0开始编号,则对任一编号为i (0≤i<n)的结点X有:
若i=0,则结点X是根;若i> 0,则X的双亲的编号为 。
若2i+1<n,则结点X的左孩子编号为2i+1,否则,结点X无左孩子(且无右孩子)。
若2i+2<n,则结点X的右孩子的编号为2i+2,否则,X无右孩子。
27.己知二叉树T如题27图所示。
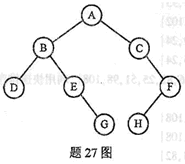
请问答下列问题:
(1)画出该二叉树对应的森林。
(2)写出对森林进行前序遍历的遍历序列i
【答案】
(1)
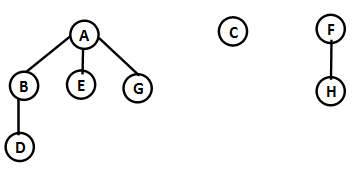
(2)ABDEGCFH
【解析】
将一棵二叉树转换为森林可以按下列步骤进行:
① 去掉二叉树的右子树,将去掉右子树后剩下的二叉树转换为一棵树(剩下的二叉树的右子树与上一个结点相连)。
② 将在第①步中被去掉的右子树再执行第①步。
③ 重复前两步,直到转换完成。
将一棵二叉树转换为树可以按下列步骤进行:
① 若某结点是其双亲结点的左孩子,则将该结点的右孩子以及当且仅当连续地沿着此右孩子的右子树方向不断地搜索到的所有右孩子,都分别与该结点的双亲结点用虚线连接起来。
② 删去原二叉树中所有双亲结点与其右孩子的连线。
③ 将图形规整化,使各结点按层次排列,并且将虚线改成实线。
前序遍历森林的原则:若森林非空,则:
①访问森林中第一棵树的根结点;
②前序遍历第一棵树中根结点的各子树所构成的森林
③前序遍历除第一棵树外其它树构成的森林。








 本文探讨了二叉树的顺序存储方式及其结点间的数学关系,详细解析了如何将二叉树转换为森林,以及森林的前序遍历方法。通过实例展示了二叉树与森林之间的转换过程,提供了深入理解数据结构的基础。
本文探讨了二叉树的顺序存储方式及其结点间的数学关系,详细解析了如何将二叉树转换为森林,以及森林的前序遍历方法。通过实例展示了二叉树与森林之间的转换过程,提供了深入理解数据结构的基础。
















 688
688

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








