UVA211 TheDomino Effect 多米诺效应

最新推荐文章于 2023-02-18 19:43:47 发布

原创最新推荐文章于 2023-02-18 19:43:47 发布 · 322 阅读

0 ·

CC 4.0 BY-SA版权

紫书第七章专栏收录该内容

35 篇文章

订阅专栏

本文介绍了一种解决双六多米诺骨牌(共28张)的所有可能排列组合问题的算法。通过搜索骨牌两端的点数(pips)，实现对所有可能布局的深度优先搜索(DFS)。代码使用C++实现，展示了如何初始化骨牌布局，进行搜索并输出所有可能的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：一副“双六”多米诺骨牌包含28张

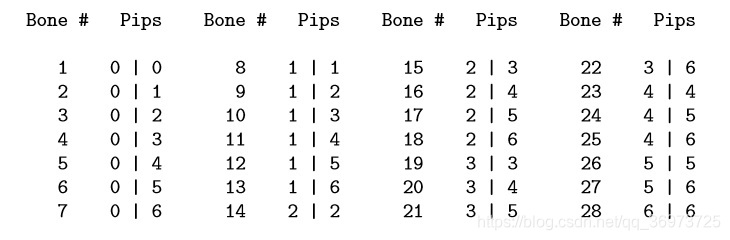
现给出一个排列，求其所有排列组合。

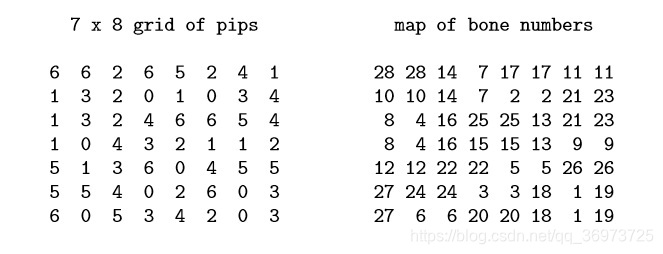
输出所有可能的右图

分析：有两种方法可做，区别就是搜索对象，第一种是搜索pips，每次只需要列举pips的两个编号即可，第二种是搜索bones每次都从列表中判断对应的序号是否还有。博主水平有限，第二种没做出来。

以第一种情况分析，每次先搜索0~6，然后再搜索0~6对应的0~6。每次就纵坐标加一。


#include<cstdio>
#include<cstring>
#include<cctype>
#include<queue>
#include<iostream>
#include<vector>
#include<list>
#include<set>
using namespace std;

const int d[2][2] = { {1, 0}, {0, 1} };
int cas = 0, g[7][8], ans, num[7][7], vis[7][8], v[30], res[7][8];
void init() {
	ans = 0;
	memset(v, 0, sizeof(v));
	memset(vis, 0, sizeof(vis));
	for (int i = 0; i < 7; i++)
		for (int j = 0; j < 8; j++) {
			if (i == 0 && j == 0) continue;
			scanf("%d", &g[i][j]);
		}
}
bool judge(int x) {
	for (int j = 0; j < 8; j++)
		if (vis[x][j] == 0) return true;
	return false;
}
void dfs(int x, int y, int nu) {
	if (nu == 28) {
		ans++;
		for (int i = 0; i < 7; i++) {
			for (int j = 0; j < 8; j++)
				printf("%4d", res[i][j]);
			printf("\n");
		}
		printf("\n");
		return;
	}
	if (x == 7) return;
	if (y == 8) {
		if (judge(x)) return;
		dfs(x + 1, 0, nu);
		return;
	}
	if (vis[x][y]) {
		dfs(x, y + 1, nu);
		return;
	}
	for (int i = 0; i < 2; i++) {
		if (i == 0 && x == 6) continue;
		if (i == 1 && y == 7) continue;
		int xx = x + d[i][0];
		int yy = y + d[i][1];
		if (vis[xx][yy]) continue;
		if (v[num[g[x][y]][g[xx][yy]]]) continue;
		res[x][y] = res[xx][yy] = num[g[x][y]][g[xx][yy]];
		vis[x][y] = vis[xx][yy] = v[num[g[x][y]][g[xx][yy]]] = 1;
		dfs(x, y + 1, nu + 1);
		vis[x][y] = vis[xx][yy] = v[num[g[x][y]][g[xx][yy]]] = 0;
	}
}
void solve() {
	if (cas) printf("\n\n\n");
	printf("Layout #%d:\n\n", ++cas);
	for (int i = 0; i < 7; i++) {
		for (int j = 0; j < 8; j++)
			printf("%4d", g[i][j]);
		printf("\n");
	}
	printf("\nMaps resulting from layout #%d are:\n\n", cas);
	dfs(0, 0, 0);
	printf("There are %d solution(s) for layout #%d.\n", ans, cas);
}
void table() {
	int cnt = 1;
	for (int i = 0; i <= 6; i++)
		for (int j = i; j <= 6; j++) {
			num[i][j] = num[j][i] = cnt++;
		}
}
int main() {
	table();
	while (~scanf("%d", &g[0][0])) {
		init();
		solve();
	}
	return 0;
}