日常刷题Leetcode.174 Dungeon Game

最新推荐文章于 2022-07-23 21:26:54 发布

LNGOD

最新推荐文章于 2022-07-23 21:26:54 发布

阅读量124

点赞数

CC 4.0 BY-SA版权

分类专栏： c++ 文章标签： c++

本文链接：https://blog.youkuaiyun.com/qq_36946274/article/details/80822655

c++ 专栏收录该内容

86 篇文章

订阅专栏

本文介绍了一个骑士从迷宫左上角出发，仅能向右或向下移动到达右下角救公主的问题。通过逆向动态规划的方法确定骑士需要的最小初始生命值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.
In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.

For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.

=======================================
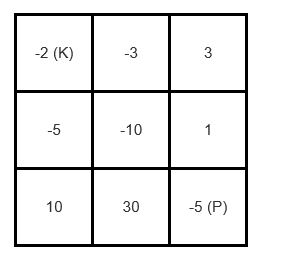
这里写图片描述

这题一看就得用动态规划，但是我一开始用的是正向动态规划，左上角到右下角的，这样做会导致只有局部优化而不是全局优化，所以部分情况会报错，比如
Input:
[[1,-3,3],[0,-2,0],[-3,-3,-3]]
Output:
5
Expected:
3
我的代码：

class Solution {//正向动态规划，仅供参考，不必详读
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m=dungeon.size();
        if(m==0)return 1;
        int n=dungeon[0].size();
        vector<vector<pair<int,int>>> work(m,vector<pair<int,int>>(n,{0,0}));
        pair<int,int>start={dungeon[0][0],min(0,dungeon[0][0])};
        work[0][0]=start;
        for(int i=1;i<m;++i){
            int first=work[i-1][0].first+dungeon[i][0];
            int second=min(work[i-1][0].second,first);
            work[i][0]={first,second};
        }
        for(int j=1;j<n;++j){
            int first=work[0][j-1].first+dungeon[0][j];
            int second=min(work[0][j-1].second,first);
            work[0][j]={first,second};
        }
        for(int i=1;i<m;++i){
            for(int j=1;j<n;++j){
                pair<int,int>minPre{0,0};
                if(work[i-1][j].second==work[i][j-1].second){
                    minPre=work[i-1][j].first>work[i][j-1].first?work[i-1][j]:work[i][j-1];
                }else if(work[i-1][j].second>work[i][j-1].second){
                    minPre=work[i-1][j];
                }else{
                    minPre=work[i][j-1];
                }
                int first=minPre.first+dungeon[i][j];
                int second=min(minPre.second,first);
                work[i][j]={first,second};
            }
        }
        return 1-work[m-1][n-1].second;
    }
};

下面给出反向动态规划代码：

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int M = dungeon.size();
    int N = dungeon[0].size();
    vector<vector<int> > minHP(M,vector<int> (N));

    if(dungeon[M-1][N-1]>=0) minHP[M-1][N-1] = 0;
    else minHP[M-1][N-1] = -dungeon[M-1][N-1];

    for(int i = M-2 ; i>=0  ; i--) //对 第 N 列 进行处理 
    {
        minHP[i][N-1] = dungeon[i][N-1]>=minHP[i+1][N-1]? 0 : minHP[i+1][N-1] - dungeon[i][N-1];
    }

    for(int j = N-2 ; j>= 0 ; j--) // 对 第 M 行 进行处理 
    {
        minHP[M-1][j] = dungeon[M-1][j]>=minHP[M-1][j+1]? 0 : minHP[M-1][j+1] - dungeon[M-1][j];
    }

    for(int i = M-2 ; i>= 0 ; i--)
        for(int j = N-2 ; j >=0  ; j--)
        {

            int minHP_from_bot = dungeon[i][j]>=minHP[i+1][j]? 0 : minHP[i+1][j] - dungeon[i][j];;
            int minHP_from_right = dungeon[i][j]>=minHP[i][j+1]? 0 : minHP[i][j+1] - dungeon[i][j];
            minHP[i][j]= min(minHP_from_bot,minHP_from_right);
        }



    return minHP[0][0]+1;
    }
};