基于matlab的K-means聚类算法

最新推荐文章于 2025-03-17 11:39:49 发布
最新推荐文章于 2025-03-17 11:39:49 发布
阅读量1.4k 收藏 8
点赞数
文章标签： 聚类 matlab
原文链接：https://blog.youkuaiyun.com/wys7541/article/details/82153844
版权

K-means聚类算法的一般步骤：

  1. 初始化。输入基因表达矩阵作为对象集X，输入指定聚类类数N，并在X中随机选取N个对象作为初始聚类中心。设定迭代中止条件，比如最大循环次数或者聚类中心收敛误差容限。
  2. 进行迭代。根据相似度准则将数据对象分配到最接近的聚类中心，从而形成一类。初始化隶属度矩阵。
  3. 更新聚类中心。然后以每一类的平均向量作为新的聚类中心，重新分配数据对象。
  4. 反复执行第二步和第三步直至满足中止条件。

下面来看看K-means是如何工作的：

图中圆形为聚类中心，方块为待聚类数据，步骤如下：

 (a)选取聚类中心，可以任意选取，也可以通过直方图进行选取。我们选择三个聚类中心，并将数据样本聚到离它最近的中心；

 (b)数据中心移动到它所在类别的中心；

 (c)数据点根据最邻近规则重新聚到聚类中心；

 (d)再次更新聚类中心；不断重复上述过程直到评价标准不再变化

评价标准：

           

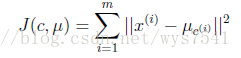
K-means面临的问题以及解决办法：

1.它不能保证找到定位聚类中心的最佳方案，但是它能保证能收敛到某个解决方案（不会无限迭代）。

   解决方法：多运行几次K-means,每次初始聚类中心点不同，最后选择方差最小的结果。

2.它无法指出使用多少个类别。在同一个数据集中，例如上图例，选择不同初始类别数获得的最终结果是不同的。

    解决方法：首先设类别数为1，然后逐步提高类别数，在每一个类别数都用上述方法，一般情况下，总方差会很快下降，直到到达一个拐点；这意味着再增加一个聚类中心不会显著减少方差，保存此时的聚类数。

MATLAB函数Kmeans

使用方法：
Idx=Kmeans(X,K)
[Idx,C]=Kmeans(X,K) 
[Idx,C,sumD]=Kmeans(X,K) 
[Idx,C,sumD,D]=Kmeans(X,K) 
[…]=Kmeans(…,’Param1’,Val1,’Param2’,Val2,…)

各输入输出参数介绍：
X: N*P的数据矩阵，N为数据个数，P为单个数据维度
K: 表示将X划分为几类，为整数
Idx: N*1的向量，存储的是每个点的聚类标号
C: K*P的矩阵，存储的是K个聚类质心位置
sumD: 1*K的和向量，存储的是类间所有点与该类质心点距离之和
D: N*K的矩阵，存储的是每个点与所有质心的距离

[…]=Kmeans(…,'Param1',Val1,'Param2',Val2,…)
这其中的参数Param1、Param2等，主要可以设置为如下：
1. ‘Distance’(距离测度)
    ‘sqEuclidean’ 欧式距离（默认时，采用此距离方式）
    ‘cityblock’ 绝度误差和，又称：L1
    ‘cosine’ 针对向量
    ‘correlation’  针对有时序关系的值
    ‘Hamming’ 只针对二进制数据
2. ‘Start’（初始质心位置选择方法）
    ‘sample’ 从X中随机选取K个质心点
    ‘uniform’ 根据X的分布范围均匀的随机生成K个质心
    ‘cluster’ 初始聚类阶段随机选择10%的X的子样本（此方法初始使用’sample’方法）
     matrix 提供一K*P的矩阵，作为初始质心位置集合
3. ‘Replicates’（聚类重复次数）  整数

案例一：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %随机获取
     
     150个点
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     X = [randn(
     
     50,
     
     2)+ones(
     
     50,
     
     2);randn(
     
     50,
     
     2)-ones(
     
     50,
     
     2);randn(
     
     50,
     
     2)+[ones(
     
     50,
     
     1),-ones(
     
     50,
     
     1)]];
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     opts = statset(
     
     'Display',
     
     'final');
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %调用Kmeans函数
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %X N*P的数据矩阵
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %Idx N*
     
     1的向量,存储的是每个点的聚类标号
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %Ctrs K*P的矩阵,存储的是K个聚类质心位置
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %SumD 
     
     1*K的和向量,存储的是类间所有点与该类质心点距离之和
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %D N*K的矩阵，存储的是每个点与所有质心的距离;
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  12. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     [Idx,Ctrs,SumD,D] = kmeans(X,
     
     3,
     
     'Replicates',
     
     3,
     
     'Options',opts);
    
    
    
   
   
  13. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  14. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %画出聚类为
     
     1的点。X(Idx==
     
     1,
     
     1),为第一类的样本的第一个坐标；X(Idx==
     
     1,
     
     2)为第二类的样本的第二个坐标
    
    
    
   
   
  15. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plot(X(Idx==
     
     1,
     
     1),X(Idx==
     
     1,
     
     2),
     
     'r.',
     
     'MarkerSize',
     
     14)
    
    
    
   
   
  16. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     hold on
    
    
    
   
   
  17. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plot(X(Idx==
     
     2,
     
     1),X(Idx==
     
     2,
     
     2),
     
     'b.',
     
     'MarkerSize',
     
     14)
    
    
    
   
   
  18. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     hold on
    
    
    
   
   
  19. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plot(X(Idx==
     
     3,
     
     1),X(Idx==
     
     3,
     
     2),
     
     'g.',
     
     'MarkerSize',
     
     14)
    
    
    
   
   
  20. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  21. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %绘出聚类中心点,kx表示是圆形
    
    
    
   
   
  22. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plot(Ctrs(:,
     
     1),Ctrs(:,
     
     2),
     
     'kx',
     
     'MarkerSize',
     
     14,
     
     'LineWidth',
     
     4)
    
    
    
   
   
  23. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plot(Ctrs(:,
     
     1),Ctrs(:,
     
     2),
     
     'kx',
     
     'MarkerSize',
     
     14,
     
     'LineWidth',
     
     4)
    
    
    
   
   
  24. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     plot(Ctrs(:,
     
     1),Ctrs(:,
     
     2),
     
     'kx',
     
     'MarkerSize',
     
     14,
     
     'LineWidth',
     
     4)
    
    
    
   
   
  25. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  26. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     legend(
     
     'Cluster 1',
     
     'Cluster 2',
     
     'Cluster 3',
     
     'Centroids',
     
     'Location',
     
     'NW')
    
    
    
   
   
  27. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
     
    
    
    
   
   
  28. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     Ctrs
    
    
    
   
   
  29. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     SumD

结果图片：

案例二：


 
 
  1. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %K-means聚类
    
    
    
   
   
  2. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     clc,clear;
    
    
    
   
   
  3. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     load tyVector;
    
    
    
   
   
  4. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     X=tyVector
     
     '; %列向量变成行向量,209*180矩阵
    
    
    
   
   
  5. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     [x,y]=size(X);
    
    
    
   
   
  6. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     opts = statset('Display
     
     ','final
     
     ');
    
    
    
   
   
  7. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     K=11;           %将X划分为K类
    
    
    
   
   
  8. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     repN=50;        %迭代次数
    
    
    
   
   
  9. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     
    
    
    
   
   
  10. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %K-mean聚类
    
    
    
   
   
  11. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     [Idx,Ctrs,SumD,D] = kmeans(X,K,'Replicates
     
     ',repN,'Options
     
     ',opts);
    
    
    
   
   
  12. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %Idx N*1的向量,存储的是每个点的聚类标号
    
    
    
   
   
  13. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     
    
    
    
   
   
  14. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     %打印结果
    
    
    
   
   
  15. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     fprintf('划分成%d类的结果如下：\n
     
     ',K)
    
    
    
   
   
  16. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     for i=1:K
    
    
    
   
   
  17. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
         tm=find(Idx==i); %求第i类的对象
    
    
    
   
   
  18. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
         tm=reshape(tm,1,length(tm)); %变成行向量
    
    
    
   
   
  19. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
         fprintf('第%d类共%d个分别是%s\n
     
     ',i,length(tm),int2str(tm)); %显示分类结果
    
    
    
   
   
  20. 
   
   
    
    
    
    
   
   
    
   
   
    
    
    
    
     
     end
    
    
    
   
   

 
 

  •                     <li class="tool-item tool-active is-like "><a href="javascript:;"><svg class="icon" aria-hidden="true">
                        <use xlink:href="#csdnc-thumbsup"></use>
                    </svg><span class="name">点赞</span>
                    <span class="count">9</span>
                    </a></li>
                    <li class="tool-item tool-active is-collection "><a href="javascript:;" data-report-click="{&quot;mod&quot;:&quot;popu_824&quot;}"><svg class="icon" aria-hidden="true">
                        <use xlink:href="#icon-csdnc-Collection-G"></use>
                    </svg><span class="name">收藏</span></a></li>
                    <li class="tool-item tool-active is-share"><a href="javascript:;"><svg class="icon" aria-hidden="true">
                        <use xlink:href="#icon-csdnc-fenxiang"></use>
                    </svg>分享</a></li>
                    <!--打赏开始-->
                                            <!--打赏结束-->
                                            <li class="tool-item tool-more">
                        <a>
                        <svg t="1575545411852" class="icon" viewBox="0 0 1024 1024" version="1.1" xmlns="http://www.w3.org/2000/svg" p-id="5717" xmlns:xlink="http://www.w3.org/1999/xlink" width="200" height="200"><defs><style type="text/css"></style></defs><path d="M179.176 499.222m-113.245 0a113.245 113.245 0 1 0 226.49 0 113.245 113.245 0 1 0-226.49 0Z" p-id="5718"></path><path d="M509.684 499.222m-113.245 0a113.245 113.245 0 1 0 226.49 0 113.245 113.245 0 1 0-226.49 0Z" p-id="5719"></path><path d="M846.175 499.222m-113.245 0a113.245 113.245 0 1 0 226.49 0 113.245 113.245 0 1 0-226.49 0Z" p-id="5720"></path></svg>
                        </a>
                        <ul class="more-box">
                            <li class="item"><a class="article-report">文章举报</a></li>
                        </ul>
                    </li>
                                        </ul>
            </div>
                        </div>
        <div class="person-messagebox">
            <div class="left-message"><a href="https://blog.youkuaiyun.com/wys7541">
                <img src="https://profile.csdnimg.cn/2/5/7/3_wys7541" class="avatar_pic" username="wys7541">
                                        <img src="https://g.csdnimg.cn/static/user-reg-year/2x/2.png" class="user-years">
                                </a></div>
            <div class="middle-message">
                                    <div class="title"><span class="tit"><a href="https://blog.youkuaiyun.com/wys7541" data-report-click="{&quot;mod&quot;:&quot;popu_379&quot;}" target="_blank">勿幻想</a></span>
                                        </div>
                <div class="text"><span>发布了49 篇原创文章</span> · <span>获赞 109</span> · <span>访问量 18万+</span></div>
            </div>
                            <div class="right-message">
                                        <a href="https://im.youkuaiyun.com/im/main.html?userName=wys7541" target="_blank" class="btn btn-sm btn-red-hollow bt-button personal-letter">私信
                    </a>
                                                        <a class="btn btn-sm  bt-button personal-watch" data-report-click="{&quot;mod&quot;:&quot;popu_379&quot;}">关注</a>
                                </div>
                        </div>
                </div>
基于MATLAB实现的K-means聚类算法
BUG？不存在的！
06-21 876
K-Means聚类算法是一种常用的无监督学习算法，其主要目标是将n个样本数据分成k个簇（cluster），并且每一个簇之间的元素相似度高，不同簇的元素相似度低。在这篇文章中，我们将使用MATLAB来实现K-Means聚类算法，并对算法进行仿真与分析。在实现K-Means算法之前，我们需要准备数据集。结果可视化后，我们可以看到数据集被分成了3个簇，每个簇之间的元素相似度较高。在完成聚类算法后，我们需要对结果进行可视化处理，以便更好地理解聚类结果。基于MATLAB实现的K-means聚类算法。
Matlab用k-means实现聚类算法
10-05
当初打数学建模的时候，在网上找了一堆东西。翻出来了这个，现在放到网上，供大家一起学习，没办法最低就1个积分了。欢迎大家一起学习！
Matlab实现K-Means聚类算法
weixin_30920513的博客
10-27 438
人生如戏！！！！ 一、理论准备 聚类算法，不是分类算法。分类算法是给一个数据，然后判断这个数据属于已分好的类中的具体哪一类。聚类算法是给一大堆原始数据，然后通过算法将其中具有相似特征的数据聚为一类。 K-Means算法的基本思想是初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心，从而确定新的簇心。一直迭代，直...
Matlab实现K均值聚类算法全面指南
最新发布
weixin_42181686的博客
03-17 737
K均值聚类是一种将数据集划分为K个簇的经典算法。它将数据点划分为具有相似特征的多个组，这些组被称为“簇”，使得组内数据的相似度高于组间。这种算法在数据挖掘和统计学中有着广泛的应用。通过以上示例和解释，你已经初步了解了Matlab中kmeans函数的使用方法。接下来章节将会深入探讨二维和三维数据的K均值聚类原理和实现细节。此外，我们还将探索高维数据聚类带来的挑战，并给出解决策略。通过这些章节的学习，你会更加熟练地运用kmeans函数在不同的数据集上进行有效的聚类分析。
Kmeans聚类算法——Matlab
m0_69715013的博客
04-24 3149
matlab实现Kmeans聚类算法+过程、结果可视化
K-means聚类 —— matlab
热门推荐
PY洋洋
02-16 4万+
1.简介 2.算法原理 3.实例分析 3.1 读取数据 3.2原理推导K均值过程 3.3 自带kmeans函数求解过程 完整代码
MATLAB实现K-means聚类
09-20
function [idx, C, sumD, D] = kmeans(X, k, varargin) % varargin：实际输入参量 if nargin 1 % 大于1刚至少有一种距离 error(sprintf(&#39;Ambiguous &#39;&#39;distance&#39;&#39; parameter value: %s.&#39;, distance)); elseif isempty(i) % 如果是空的，则表明没有合适的距离 error(sprintf(&#39;Unknown &#39;&#39;distance&#39;&#39; parameter value: %s.&#39;, distance)); end % 针对不同的距离，处理不同 distance = distNames{i}; switch distance case &#39;cityblock&#39; % sort 列元素按升序排列，Xord中存的是元素在原始矩阵中的列中对应的大小位置 [Xsort,Xord] = sort(X,1); case &#39;cosine&#39; % 余弦 % 计算每一行的和的平方根 Xnorm = sqrt(sum(X.^2, 2)); if any(min(Xnorm) <= eps * max(Xnorm)) error([&#39;Some points have small relative magnitudes, making them &#39;, ... &#39;effectively zero.\nEither remove those points, or choose a &#39;, ... &#39;distance other than &#39;&#39;cosine&#39;&#39;.&#39;], []); end % 标量化 Xnorm(:,ones(1,p))得到n*p的矩阵 X = X ./ Xnorm(:,ones(1,p)); case &#39;correlation&#39; % 线性化 X = X - repmat(mean(X,2),1,p); % 计算每一行的和的平方根 Xnorm = sqrt(sum(X.^2, 2)); if any(min(Xnorm) 1 error(sprintf(&#39;Ambiguous &#39;&#39;start&#39;&#39; parameter value: %s.&#39;, start)); elseif isempty(i) error(sprintf(&#39;Unknown &#39;&#39;start&#39;&#39; parameter value: %s.&#39;, start)); elseif isempty(k) error(&#39;You must specify the number of clusters, K.&#39;); end start = startNames{i}; % strcmp比较两个字符串 uniform是在X中随机选择K个点 if strcmp(start, &#39;uniform&#39;) if strcmp(distance, &#39;hamming&#39;) error(&#39;Hamming distance cannot be initialized with uniform random values.&#39;); end % 标量化后的X Xmins = min(X,1); Xmaxs = max(X,1); end elseif isnumeric(start) % 判断输入是否是一个数 这里的start是一个K*P的矩阵，表示初始聚类中心 CC = start; % CC表示初始聚类中心 start = &#39;numeric&#39;; if isempty(k) k = size(CC,1); elseif k ~= size(CC,1); error(&#39;The &#39;&#39;start&#39;&#39; matrix must have K rows.&#39;); elseif size(CC,2) ~= p error(&#39;The &#39;&#39;start&#39;&#39; matrix must have the same number of columns as X.&#39;); end if isempty(reps) reps = size(CC,3); elseif reps ~= size(CC,3); error(&#39;The third dimension of the &#39;&#39;start&#39;&#39; array must match the &#39;&#39;replicates&#39;&#39; parameter value.&#39;); end % Need to center explicit starting points for &#39;correlation&#39;. % 线性距离需要指定具体的开始点 % (Re)normalization for &#39;cosine&#39;/&#39;correlation&#39; is done at each % iteration.每一次迭代进行“余弦和线性”距离正规化 % 判断是否相等 if isequal(distance, &#39;correlation&#39;) % repmat复制矩阵1*P*1 线性化 CC = CC - repmat(mean(CC,2),[1,p,1]); end else error(&#39;The &#39;&#39;start&#39;&#39; parameter value must be a string or a numeric matrix or array.&#39;); end % ------------------------------------------------------------------ % 如果一个聚类丢失了所有成员，这个进程将被调用 if ischar(emptyact) emptyactNames = {&#39;error&#39;,&#39;drop&#39;,&#39;singleton&#39;}; i = strmatch(lower(emptyact), emptyactNames); if length(i) > 1 error(sprintf(&#39;Ambiguous &#39;&#39;emptyaction&#39;&#39; parameter value: %s.&#39;, emptyact)); elseif isempty(i) error(sprintf(&#39;Unknown &#39;&#39;emptyaction&#39;&#39; parameter value: %s.&#39;, emptyact)); end emptyact = emptyactNames{i}; else error(&#39;The &#39;&#39;emptyaction&#39;&#39; parameter value must be a string.&#39;); end % ------------------------------------------------------------------ % 控制输出的显示示信息 if ischar(display) % strvcat 垂直连接字符串 i = strmatch(lower(display), strvcat(&#39;off&#39;,&#39;notify&#39;,&#39;final&#39;,&#39;iter&#39;)); if length(i) > 1 error(sprintf(&#39;Ambiguous &#39;&#39;display&#39;&#39; parameter value: %s.&#39;, display)); elseif isempty(i) error(sprintf(&#39;Unknown &#39;&#39;display&#39;&#39; parameter value: %s.&#39;, display)); end display = i-1; else error(&#39;The &#39;&#39;display&#39;&#39; parameter value must be a string.&#39;); end % ------------------------------------------------------------------ % 输入参数K的控制 if k == 1 error(&#39;The number of clusters must be greater than 1.&#39;); elseif n 2 % &#39;iter&#39;,\t 表示向后空出8个字符 disp(sprintf(&#39; iter\t phase\t num\t sum&#39;)); end % ------------------------------------------------------------------ % Begin phase one: batch reassignments 第一队段：分批赋值 converged = false; iter = 0; while true % Compute the distance from every point to each cluster centroid % 计算每一个点到每一个聚类中心的距离，D中存放的是N*K个数值 D(:,changed) = distfun(X, C(changed,:), distance, iter); % Compute the total sum of distances for the current configuration. % Can&#39;t do it first time through, there&#39;s no configuration yet. % 计算当前配置的总距离，但第一次不能执行，因为还没有配置 if iter > 0 totsumD = sum(D((idx-1)*n + (1:n)&#39;)); % Test for a cycle: if objective is not decreased, back out % the last step and move on to the single update phase % 循环测试：如果目标没有减少，退出到最后一步，移动到第二阶段 % prevtotsumD表示前一次的总距离，如果前一次的距离比当前的小，则聚类为上一次的，即不发生变化 if prevtotsumD 2 % &#39;iter&#39; disp(sprintf(dispfmt,iter,1,length(moved),totsumD)); end if iter >= maxit, % break（2） break; % 跳出while end end % Determine closest cluster for each point and reassign points to clusters % 决定每一个点的最近分簇，重新分配点到各个簇 previdx = idx; % 大小为n*1 % totsumD 被初始化为无穷大，这里表示总距离 prevtotsumD = totsumD; % 返回每一行中最小的元素，d的大小为n*1，nidx为最小元素在行中的位置，其大小为n*1，D为n*p [d, nidx] = min(D, [], 2); if iter == 0 % iter==0,表示第一次迭代 % Every point moved, every cluster will need an update % 每一个点需要移动，每一个簇更新 moved = 1:n; idx = nidx; changed = 1:k; else % Determine which points moved 决定哪一个点移动 % 找到上一次和当前最小元素不同的位置 moved = find(nidx ~= previdx); if length(moved) > 0 % Resolve ties in favor of not moving % 重新分配而不是移动 括号中是一个逻辑运算 确定需要移动点的位置 moved = moved(D((previdx(moved)-1)*n + moved) > d(moved)); end % 如果没有不同的，即当前的是最小元素，跳出循环，得到的元素已经是各行的最小值 if length(moved) == 0 % break（3） break; end idx(moved) = nidx(moved); % Find clusters that gained or lost members 找到获得的或者丢失的成员的分簇 % 得到idx(moved)和previdx(moved)中不重复出现的所有元素，并按升序排列 changed = unique([idx(moved); previdx(moved)])&#39;; end % Calculate the new cluster centroids and counts. 计算新的分簇中心和计数 % C(changed,:)表示新的聚类中心，m(changed)表示聚类标号在idx中出现的次数 % sort 列元素按升序排列，Xsort存放对的元素，Xord中存的是元素在原始矩阵中的列中对应的大小位置 [C(changed,:), m(changed)] = gcentroids(X, idx, changed, distance, Xsort, Xord); iter = iter + 1; % Deal with clusters that have just lost all their members % 处理丢失所有成员的分簇，empties表示丢失元素的聚类标号 不用考虑 empties = changed(m(changed) == 0); if ~isempty(empties) switch emptyact case &#39;error&#39; % 默认值，一般情况下不会出现 error(sprintf(&#39;Empty cluster created at iteration %d.&#39;,iter)); case &#39;drop&#39; % Remove the empty cluster from any further processing % 移走空的聚类 D(:,empties) = NaN; changed = changed(m(changed) > 0); if display > 0 warning(sprintf(&#39;Empty cluster created at iteration %d.&#39;,iter)); end case &#39;singleton&#39; if display > 0 warning(sprintf(&#39;Empty cluster created at iteration %d.&#39;,iter)); end for i = empties % Find the point furthest away from its current cluster. % Take that point out of its cluster and use it to create % a new singleton cluster to replace the empty one. % 找到离聚类中心最远距离的点，把该点从它的聚类中移走，用它来创建一个新的聚类，来代替空的聚类 % 得到列的最大元素（dlarge），以及该元素在列中的标号（lonely） [dlarge, lonely] = max(d); from = idx(lonely); % taking from this cluster 从当前聚类移走 C(i,:) = X(lonely,:); m(i) = 1; idx(lonely) = i; d(lonely) = 0; % Update clusters from which points are taken % 更新那些点被移走的聚类 [C(from,:), m(from)] = gcentroids(X, idx, from, distance, Xsort, Xord); changed = unique([changed from]); end end end end % phase one % ------------------------------------------------------------------ % Initialize some cluster information prior to phase two % 为第二阶段初始化一些先验聚类信息 针对特定的距离，默认的是欧氏距离 switch distance case &#39;cityblock&#39; Xmid = zeros([k,p,2]); for i = 1:k if m(i) > 0 % Separate out sorted coords for points in i&#39;th cluster, % and save values above and below median, component-wise % 分解出第i个聚类中挑选的点的坐标，保存它的上，下中位数 % reshape把矩阵分解为要求的行列数m*p % sort 列元素按升序排列，Xord中存的是元素在原始矩阵中的列中对应的大小位置 Xsorted = reshape(Xsort(idx(Xord)==i), m(i), p); % floor取比值小或者等于的最近的值 nn = floor(.5*m(i)); if mod(m(i),2) == 0 Xmid(i,:,1:2) = Xsorted([nn, nn+1],:)&#39;; elseif m(i) > 1 Xmid(i,:,1:2) = Xsorted([nn, nn+2],:)&#39;; else Xmid(i,:,1:2) = Xsorted([1, 1],:)&#39;; end end end case &#39;hamming&#39; Xsum = zeros(k,p); for i = 1:k if m(i) > 0 % Sum coords for points in i&#39;th cluster, component-wise % 对基于分量对第i个聚类的坐标点求和 Xsum(i,:) = sum(X(idx==i,:), 1); end end end % ------------------------------------------------------------------ % Begin phase two: single reassignments 第二阶段：单独赋值 % m中保存的是每一个聚类的个数，元素和为n % find(m&#39; > 0)得到m&#39;中大于0的元素的位置（索引） % 实际情况（默认情况下）changed=1:k changed = find(m&#39; > 0); lastmoved = 0; nummoved = 0; iter1 = iter; while iter < maxit % Calculate distances to each cluster from each point, and the % potential change in total sum of errors for adding or removing % each point from each cluster. Clusters that have not changed % membership need not be updated. % 计算从每一个点到每一个聚类的距离，潜在由于总距离发生变化移除或添加引起的错误。 % 那些成员没有改变的聚类不需要更新。 % % Singleton clusters are a special case for the sum of dists % calculation. Removing their only point is never best, so the % reassignment criterion had better guarantee that a singleton % point will stay in its own cluster. Happily, we get % Del(i,idx(i)) == 0 automatically for them. % 单独聚类在计算距离时是一个特殊情况，仅仅移除点不是最好的方法，因此重新赋值准则能够保证一个 % 单独的点能够留在它的聚类中，可喜的是，自动有Del(i,idx(i)) == 0。 switch distance case &#39;sqeuclidean&#39; for i = changed % idx存放的距离矩阵D中每一行的最小元素所处的列，也即位置 mbrs = (idx == i); sgn = 1 - 2*mbrs; % -1 for members, 1 for nonmembers % 表示只有一个聚类 if m(i) == 1 % prevent divide-by-zero for singleton mbrs 防止单个成员做0处理 sgn(mbrs) = 0; end Del(:,i) = (m(i) ./ (m(i) + sgn)) .* sum((X - C(repmat(i,n,1),:)).^2, 2); end case &#39;cityblock&#39; for i = changed if mod(m(i),2) == 0 % this will never catch singleton clusters ldist = Xmid(repmat(i,n,1),:,1) - X; rdist = X - Xmid(repmat(i,n,1),:,2); mbrs = (idx == i); sgn = repmat(1-2*mbrs, 1, p); % -1 for members, 1 for nonmembers Del(:,i) = sum(max(0, max(sgn.*rdist, sgn.*ldist)), 2); else Del(:,i) = sum(abs(X - C(repmat(i,n,1),:)), 2); end end case {&#39;cosine&#39;,&#39;correlation&#39;} % The points are normalized, centroids are not, so normalize them normC(changed) = sqrt(sum(C(changed,:).^2, 2)); if any(normC 0 % Resolve ties in favor of not moving % 重新分配而不是移动 确定移动的位置 moved = moved(Del((previdx(moved)-1)*n + moved) > minDel(moved)); end if length(moved) == 0 % Count an iteration if phase 2 did nothing at all, or if we&#39;re % in the middle of a pass through all the points if (iter - iter1) == 0 | nummoved > 0 iter = iter + 1; if display > 2 % &#39;iter&#39; disp(sprintf(dispfmt,iter,2,nummoved,totsumD)); end end converged = true; break; end % Pick the next move in cyclic order moved = mod(min(mod(moved - lastmoved - 1, n) + lastmoved), n) + 1; % If we&#39;ve gone once through all the points, that&#39;s an iteration if moved 2 % &#39;iter&#39; disp(sprintf(dispfmt,iter,2,nummoved,totsumD)); end if iter >= maxit, break; end nummoved = 0; end nummoved = nummoved + 1; lastmoved = moved; oidx = idx(moved); nidx = nidx(moved); totsumD = totsumD + Del(moved,nidx) - Del(moved,oidx); % Update the cluster index vector, and rhe old and new cluster % counts and centroids idx(moved) = nidx; m(nidx) = m(nidx) + 1; m(oidx) = m(oidx) - 1; switch distance case &#39;sqeuclidean&#39; C(nidx,:) = C(nidx,:) + (X(moved,:) - C(nidx,:)) / m(nidx); C(oidx,:) = C(oidx,:) - (X(moved,:) - C(oidx,:)) / m(oidx); case &#39;cityblock&#39; for i = [oidx nidx] % Separate out sorted coords for points in each cluster. % New centroid is the coord median, save values above and % below median. All done component-wise. Xsorted = reshape(Xsort(idx(Xord)==i), m(i), p); nn = floor(.5*m(i)); if mod(m(i),2) == 0 C(i,:) = .5 * (Xsorted(nn,:) + Xsorted(nn+1,:)); Xmid(i,:,1:2) = Xsorted([nn, nn+1],:)&#39;; else C(i,:) = Xsorted(nn+1,:); if m(i) > 1 Xmid(i,:,1:2) = Xsorted([nn, nn+2],:)&#39;; else Xmid(i,:,1:2) = Xsorted([1, 1],:)&#39;; end end end case {&#39;cosine&#39;,&#39;correlation&#39;} C(nidx,:) = C(nidx,:) + (X(moved,:) - C(nidx,:)) / m(nidx); C(oidx,:) = C(oidx,:) - (X(moved,:) - C(oidx,:)) / m(oidx); case &#39;hamming&#39; % Update summed coords for points in each cluster. New % centroid is the coord median. All done component-wise. Xsum(nidx,:) = Xsum(nidx,:) + X(moved,:); Xsum(oidx,:) = Xsum(oidx,:) - X(moved,:); C(nidx,:) = .5*sign(2*Xsum(nidx,:) - m(nidx)) + .5; C(oidx,:) = .5*sign(2*Xsum(oidx,:) - m(oidx)) + .5; end changed = sort([oidx nidx]); end % phase two % ------------------------------------------------------------------ if (~converged) & (display > 0) warning(sprintf(&#39;Failed to converge in %d iterations.&#39;, maxit)); end % Calculate cluster-wise sums of distances nonempties = find(m(:)&#39;>0); D(:,nonempties) = distfun(X, C(nonempties,:), distance, iter); d = D((idx-1)*n + (1:n)&#39;); sumD = zeros(k,1); for i = 1:k sumD(i) = sum(d(idx == i)); end if display > 1 % &#39;final&#39; or &#39;iter&#39; disp(sprintf(&#39;%d iterations, total sum of distances = %g&#39;,iter,totsumD)); end % Save the best solution so far if totsumD 3 Dbest = D; end end end % Return the best solution
基于K-means聚类算法的图像分割(MATLAB实现).rar_ASV聚类_K-Means图像分割_k means_rest
07-14
《基于K-means聚类算法的图像分割在MATLAB中的实现》 图像分割是计算机视觉领域中的基础任务，它旨在将图像划分为多个区域或对象，每个区域具有相似的特征。K-means聚类算法是一种广泛应用的数据分析方法，它通过...
聚类算法：K-means聚类图像分割
12-22
下面是K-Means聚类算法的分析流程，步骤如下： 第一步，确定K值，即将数据集聚集成K个类簇或小组。 第二步，从数据集中随机选择K个数据点作为质心（Centroid）或数据中心。 第三步，分别计算每个点到每个质心之间的...
基于K-means聚类算法的图像分割及其MATLAB实现
03-05
基于K-means聚类算法的图像分割 算法的基本原理：  基于K-means聚类算法的图像分割以图像中的像素为数据点，按照指定的簇数进行聚类，然后将每个像素点以其对应的聚类中心替代，重构该图像。 算法步骤： ①随机选取...
基于k-means聚类方法和DTW算法结合起来分析时间序列类型的用户用电数据源码+项目说明.zip
05-31
基于DTW距离的时间序列聚类算法，与传统的k-means算法相比，能够处理非线性对齐的时间序列，因此适用于更广泛的应用领域。 实验 主要步骤： 手工挑选训练集，减少过于离散的样本 进行数据预处理，包括处理样本中无...
基于流形距离的K-means聚类算法（matlab实现）
12-30
将流形距离引入K-means聚类算法中，对于具有流形结构的数据集有很好的聚类效果，流形距离计算参数的设定充分考虑了全局和局部一致性。
K-means聚类分析（MatlabGUI）
07-31
自己写的一个很有用的Kmeans演示Demo，使用MATLAB写的，有各种酷炫功能，值得大家下载来玩一玩。
k-means聚类matlab代码
01-17
简单的k-means聚类算法代码，matlab直接打开可用。里面注释什么都很详细，新手也可以简单上手！
K-means聚类算法 matlab实现
01-18
K-means聚类算法利用matlab实现，可以查看每次迭代的效果
Matlab实现Kmeans聚类算法
qq_37904531的博客
02-01 3万+
matlab实现kmeans聚类算法
基于Matlab实现k-means聚类算法
2301_78484069的博客
07-18 1709
K-means算法是一种基于贪心思想的无监督聚类算法，它能够将数据集划分为k个簇，并且每个数据点都属于距离自己最近的簇。K-means聚类算法是一种非常流行的无监督聚类算法，在实际应用中得到了广泛的运用。假设我们有一个二维数据集data，包含9个样本点，其中前6个样本点分别在三个不同的簇中，后三个样本点分别位于这三个簇中心点附近。从结果中可以看出，我们成功地将数据集划分为了k个簇，并且每个数据点都属于距离自己最近的簇。%对于数据集中的每个样本点，计算它与每个簇中心之间的距离，将它划分到距离最近的簇中。
k-means聚类算法（matlab实现）
qq_40276082的博客
04-18 9079
k-means聚类算法是硬聚类算法的一种，即在n纬欧几里得空间把n个样本数据分为k类。首先根据用户要确定聚类的数目k,随机性的选取k个样本，把每一个对象成为一个种子，每一个种子代表一个类的中心，对其余的每个对象，采用近邻原则，将它们赋给最近的类。重新计算在每个类中对象的均值新形成的聚类中心，重复进行这个过程直到函数式收敛为止。K-means算法是一种无监督学习算法，用于将n个数据点划分为k个簇（cluster）。该算法的主要思想是将数据点划分为k个簇，使得同一簇内的数据点彼此相似，而簇间的数据点相差较大。
MatLab Kmeans聚类
ben121_的博客
04-09 715
MatLab Kmeans聚类： https://blog.youkuaiyun.com/makenothing/article/details/50363536 Kmeans聚类算法详解： https://blog.youkuaiyun.com/qq_32892383/article/details/80107795 Kmeans聚类算法：（一维数组简单分类） https://blog.youkuaiyun.com/zengxia...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值