VGG: Very Deep Convolutional Networks for Large-Scale Image Recognition

最新推荐文章于 2025-04-10 20:21:04 发布
最新推荐文章于 2025-04-10 20:21:04 发布
阅读量540 收藏 3
点赞数
分类专栏： 论文笔记
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_36825778/article/details/102588965
版权
本文详细介绍了VGG网络，该网络在2014年ILSVRC比赛中获得分类项目亚军和定位项目冠军。VGG因其简单结构和强大特征提取能力而广泛应用，如风格迁移、目标检测。研究发现，增加网络深度、使用小卷积核和多尺度训练能有效提升性能。VGG16被证明是最优模型，通过3x3卷积层取代大卷积核和全连接层，减少了参数数量。此外，文章还探讨了感受野的概念及其在目标检测算法中的重要性，并讨论了微调在迁移学习中的作用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

一、论文研究背景、成果

1.论文研究背景

自从2012年AlexNet将深度学习的方法应用到ImageNet的图像分类比赛中并取得state of the art的惊人结果后,大家都竞相效仿并在此基础上做了大量尝试和改进
1.小卷积核
在第一个卷积层用了更小的卷积核和卷积stride (Zeiler & Fergus, 2013;Sermanet et al, 2014)
2.多尺度
训练和测试使用整张图的不同尺度(Sermanet et al., 2014;Howard, 2014) .

vgg作者不仅将上面的两种方法应用到自己的网络设计和训练测试阶段,同时还考虑了网络深度对结果的影响

2.论文研究成果

在2014年在ILSVRC比赛上获得了分类项目的第二名(第一是GoogLeNet) ,和定位项目的第一名。同时模型对其他数据集有很好的泛化能力。

VGG由于其结构简单,提取特征能力强,所以应用场景广泛

例如：
快速风格迁移算法
目标检测的backbone,提取特征(fater rcnn, ssd等)
gan网络内容特征提取,进行内容计算(内容损失是gan网络损失的一部分)
在这里插入图片描述

二、论文研究方法

进行了六组对比试验，包括A，A-LRN，B，C，D，E六种不同的网络结构

A-LRN在A的基础上加入了一个LRN层
B在A的基础上加入了两个3*3的卷积层
C在B的基础上加入了三个1*1的卷积层
D在B的基础上加入了三个3*3的卷积层
E在D的基础上加入了三个3*3的卷积层
在这里插入图片描述

单尺度测试结果对比

在这里插入图片描述
结论：
1、 LRN对网络性能提升没有帮助
2、 对于同一个网络结构多尺度训练可以提高网络精度
3、 E模型(VGG19)效果最好,一定程度加深网络可以提高网络精度

多尺度测试结果对比

在这里插入图片描述
结论:
1、对比单尺度预测,多尺度综合预测,能够提升预测的精度
证明了scale jittering(尺度抖动)的作用
2、 vgg16为best model

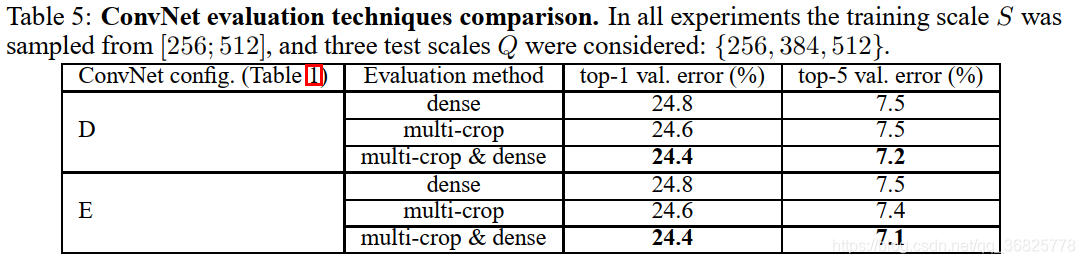
在这里插入图片描述
结论：dense evaluation & multi-crop 两种测试方式联合使用效果最好

在这里插入图片描述
结论：融合模型D、E之后模型错误率进一步下降

三、论文结论

1、在一定范围内,通过增加深度能有效地提升性能
2、最佳模型: VGG16,从头到尾只有3x3卷积与2x2池化,简洁优美
3、多个小卷积核比单个大卷积核性能好(与AlexNet对比可知)
4、AlexNet曾经用到的LRN层并没有带来性能的提升,因此在其它组的网络中均没再出现LRN层
5、尺度抖动scale jittering (多尺度训练,多尺度测试)有利于网络性能的提升

四、感受野

1.感受野概念

感受野(Receptive Field)的定义是：卷积神经网络每一层输出的特征图(feature map)上的像素点在输入图片上映射的区域大小。再通俗点的解释是,特征图上的一个点跟原图上有关系的点的区域。

感受野概念为什么重要?
感受野被称作是CNN中最重要的概念之一,目标检测流行的算法比如SSD, Faster Rcnn等中prior box和Anchor box的设计都是以感受野为依据做的设计。

示例：
在这里插入图片描述
输入原始图大小为7*7
conv1: 3*3 strides=1, valid
feature: (7-3+1)/1=5
conv2: 3*3 strides=1, valid
feature: (5-3+1)/1=3

原始输入感受野:1
conv1层感受野:3
conv2层感受野:5
如果conv1: 5*5 strides=1, valid,感受野是多少? 5

结论:
一个55卷积核感受野大小与两个33卷积核的感受野等效。
以此类推三个33的卷积核感受野与一个77卷积核的感受野等效

2.感受野的计算

感受野计算公式： r n = r n − 1 + ( k n − 1 ) ∏ i = 1 n − 1 s i r_n=r_{n-1}+(k_n-1)\prod \limits_{i=1}^{n-1}s_i rn​=rn−1​+(kn​−1)

最低0.47元/天 解锁文章
深度学习研究理解10：Very Deep Convolutional Networks for Large-Scale Image Recognition
whiteinblue的专栏
02-06 2万+
本文是牛津大学 visual geometry group（VGG）Karen Simonyan 和Andrew Zisserman 于14年撰写的论文，主要探讨了深度对于网络的重要性；并建立了一个19层的深度网络获得了很好的结果；在ILSVRC上定位第一，分类第二。 一：摘要 …… 从Alex-net发展而来的网络主要修改一下两个方面： 1，在第一个卷基层层使用更小的filter尺寸和间
VGG:VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION
MR CODER
12-13 362
VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION ImageNet2014 定位第一，分类第二 "VGG"代表，牛津大学的Oxford Visual Geometry Group VGG 的特点： （1）小卷积核：作者将卷积核全部替换为3*3，极少用了1*1 （2）小池化核：相比AlexNet的3*3的池化核，V...
Very Deep Convolutional Networks for Large-Scale Image Recognition
雨石
10-02 2万+
这篇论文是今年9月份的论文[1]，比较新，其中的观点感觉对卷积神经网络的参数调整大有指导作用，特总结之。关于卷积神经网络(Convolutional Neural Network, CNN)，笔者后会作文阐述之，读者若心急则或可用谷歌百度一下。
【论文阅读】VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION
最新发布
qq_34222839的博客
04-10 1035
VGG是由Oxford名为Visual Geometry Group的小组提出的，VGG的名字也是来自其组名首字母的缩写。VGG是ILSVRC2014的亚军，其在的基础上，使用更小的卷积核，并尝试从增加深度的方面改善其性能。
（VGG）Very Deep Convolutional Networks for Large-Scale Image Recognition
椰子奶糖的博客
07-12 706
Very Deep Convolutional Networks for Large-Scale Image Recognition 文章目录Very Deep Convolutional Networks for Large-Scale Image Recognition参考IntroductionConvNet ConfigurationsArchitectureConfigurationsDiscussionClassification FrameworkTraining（参考VGGNet 阅读理解，
论文笔记：Very deep convolutional networks for large-scale image recognition（VGG）
upup
06-05 3198
一、基本信息 标题：Very deep convolutional networks for large-scale image recognition 时间：2014 出版源：arXiv 论文领域：CNN、深度学习 引用格式：Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv:1409.1556, 2014. 二、研究背景 在
经典网络结构VGG-net《Very Deep Convolutional Networks for Large-Scale Image Recognition》
女王の专属领地
05-04 1085
论文地址：https://arxiv.org/abs/1409.1556论文翻译：http://blog.youkuaiyun.com/wangsidadehao/article/details/54311282VGG-Net来自牛津大学Andrew Zisserman 教授的组 (Oxford)，在2014年的 ILSVRC localization and classification 两个问题上分别取得...
VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION
03-01
这篇文章的标题为“VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION”，主要讨论了在大规模图像识别中，卷积神经网络（ConvNets）深度对准确率的影响。文章的核心贡献是对不同深度的网络进行了...
VGGNet：very deep convolutional networks for large-scale image recognition LCLR2015
qq_45844265的博客
01-18 636
下图每一列都是一个模型，本文提出6个网络模型，命名为A、A-LRN、B、C、D、E。如网络A，block1中卷积核大小3，个数64，在block2中卷积核大小不变，个数翻倍128个，在block3中卷积核大小不变，个数在block的基础上又翻倍变成256个，同时卷积层数从1层变成了2层。输入彩色图像信息为224×224×3，block1有64个卷积核，对输入图像做下采样，原图的长宽从224×224缩减为原来的一半，即112×112，但是通道数由64增加一半到128，block2-6依次做类似处理。
VGG： Very deep convolutional networks for large-scale image recognition
空字符
12-02 829
1 前言 经过前面两篇文章的介绍，我们已经了解了LeNet5和AlexNet网络模型。但是总体上来说两者的网络结构几乎并没有太大的差别，仅仅，同时网络的深度以及参数的规模也没有太大的变化。在接下来的这篇文章中，我们将会看到卷积网络中的第三个经典模型VGG。在这篇文章中，作者对卷积网络卷积深度的设计进行了一个探索，并且通过尝试逐步加深网络的深度来提高模型的整体性能。这使得VGG在当年的ILSVRC任务中取得了TOP1的成绩。 2 VGG网络 VGG网络产生于2014年的Visual Geometry Grou
VGG: VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION
TheWaySoFar
03-27 1254
Abstract: 我们的工作是研究更加深的卷及网络对于大规模机器学习的影响. 我们的主要贡献是使用3X3的非常小的卷积层来增加网络的深度改善其性能, 最终的深度在16~19层. 这些发现是基于14年的比赛上的提交, 队伍在目标定位和图像分类方面分别获得了第一和第二.我们同时展示了我们的网络对于别的数据集也有同样的适用性, 他们获得了世界顶尖的水平. 我们已将我们的两种性能最好的Con...
（VGG）VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION--Karen Simonyan
xu.hyj
09-01 1167
本文增加了深度，设计了从11层到19层几种VGG模型，然后通过训练集和测试集多尺度变化进一步提高了性能。在ILSVRC2014大赛上通过多模型融合取得了次于GoogleNet的第二名成绩。 总之最大的成就应当是证明了深度对于图像分类的精度是有帮助的...
VGGNet 阅读理解 - Very Deep Convolutional Networks for Large-Scale Image Recognition
热门推荐
长风破浪会有时，直挂云帆济沧海
03-19 5万+
论文理解 - VGGNet - Very Deep Convolutional Networks for Large-Scale Image Recognition [VGG-Paper] [原文地址 - Very deep convolutional networks for large-scale image recognition] 一篇对 VGGNet 理解比较详细的博客，很长...
Very Deep Convolutional Networks For Large-Scale Image Recognition(VGGnet)
励志的小胡子
03-06 1253
用于大规模图像识别的非常深的卷积神经网络 Abstract(摘要) 在这项工作中，我们研究了卷积网络深度对其在大规模图像识别设置中的准确性的影响。我们的主要贡献使使用非常小()卷积滤波器的架构对越来越深的网络进行全面评估，这表明通过将深度堆到16-19的权重层可以实现对现有技术配置的显著改进。这些发现使我么提交的ImageNet Challe...
Very Deep Convolutional Networks for Large-Scale Image Recognition(精读)
小胜爱捣鼓
11-04 3043
一.文献名字和作者     Very Deep Convolutional Networks for Large-Scale Image Recognition. Karen Simonyan,Andrew Zisserman     二.阅读时间     2014年11月4日 三.文献的目的     文献的主要目的在于测试随着深度的加深，卷积神经网络对于大规模
VGG——Very Deep Convolutional Networks for Large-Scale Image Recognition
weixin_44853840的博客
05-05 583
目录AbstractquestionmethodanswerIntroductionwhy research？ContributionDetailsArchitectureTrainingTestingConclusion Abstract question 大规模图像识别任务下卷积网络深度对其预测准确率的影响。 method 使用具有非常小的（3×3）卷积滤波器的架构对深度不断递增的网络进行全面评估。 answer 通过将权重层深度推到16-19层可以在现有技术配置下（使准确率）实现显著提升。在Image
VGG——Very deep convolutional networks for large-scale image recognition
seniusen的博客
04-20 458
1. 摘要 在使用非常小（3×3）的卷积核情况下，作者对逐渐增加网络的深度进行了全面的评估，通过设置网络层数达 16-19 层，最终效果取得了显著提升。 2. 介绍 近来，卷积神经网络在大规模图像识别领域取得了巨大的成功，这一方面归功于大规模公开数据的出现，另一方面则是计算能力的提升。在 AlexNet 的基础上大家进行了很多的尝试来进行改进，一条线是在卷积层利用更小的感知窗口和更小的步长，另...
Very Deep Convolutional Networks for Large-Scale Image Recognition" by Karen Simonyan and Andrew Zisserman (2014)
05-12
"Very Deep Convolutional Networks for Large-Scale Image Recognition" is a research paper by Karen Simonyan and Andrew Zisserman, which was published in 2014. The paper introduces the architecture of the Convolutional Neural Network (CNN) called VGGNet, which achieved state-of-the-art results in image classification tasks during the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) in 2014. VGGNet is a deep CNN architecture that consists of 16-19 layers, with a simple and uniform structure. The network has small convolution filters of size 3x3, which are stacked on top of each other to form deeper representations. The authors showed that increasing the depth of the network leads to better performance, but at a cost of increased computational complexity. The paper also introduced a method for visualizing the learned features of the network, which helped to understand how the network was able to achieve high performance on image classification tasks. The authors used the learned features of the network to generate images that maximally activate certain neurons in the network, which provided insights into the types of patterns that the network was able to recognize. Overall, the VGGNet architecture has become a popular benchmark in the field of deep learning, and has been used as a starting point for many subsequent CNN architectures.
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值