基于生成函数的外呼模块数量模型

背景：

有一个外呼任务，利用自研的机器人在规定时间内把一定数量的外呼电话全部打完，一个机器人一次只能拨打一个电话。以下是我对问题的抽象和给出的模型，可能存在错误的地方，如有发现还请指出，多谢！

问题描述

1. 总共有N通电话要打；
2. 配置m个拨打模块，由于运营商的限制，每个模块100秒内最多只能打12通电话，假设每通电话通话时长小于100s，每天打10个小时，一个模块满负荷下每天可以拨打 10 * 3600 * 12 / 100 = 4320通电话；
3. 假设每通电话的平均接听率为p，未接听电话需要后续重新拨打；
4. 用户一旦接听电话后本次任务标记完成。
   求：至少需要配备多少模块和机器人能在10天内打完N通电话

求解过程

首先假设用户之间相互独立，即A用户是否接听不受B用户影响。分两种情况讨论：

简单情况

用户个体每次接电话相互独立，即：第n次是否接听电话不受第n-1次的影响。则针对第$i$个用户的电话任务是否完成可以用下图表述：

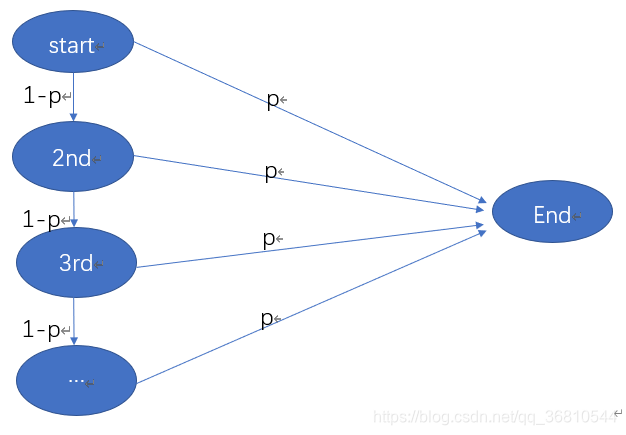
则有用户在两次内接听的概率为：$1-(1-p{)}^2$如果需要两次内用户的接听率大于99%，则有：$1-(1-p{)}^2\ge 0.99$ 解出p≥0.9，即平均接听率必须大于0.9。
在此假设下，理论上N通电话永远都无法全部完成，对于任意集合$I$，存在元素$i$每次都以(1-p)的概率选择不接听电话，则问题归约成若p≥0.9，以99%的概率打完N通电话需要拨号的模块配置数量。配置的模块数量为$\lceil \frac{2\ast N}{4320\ast 10}\rceil$，设N=100000，则模块数为5个，机器人数为60个。
但是，实际接听率p远小于90%,假设p=0.6，则至少需要拨打多次是才能保证一个用户的接听率大于99%? 有$1-(1-p{)}^n\ge 0.99$ 求n，有$n\ge \frac{log(0.01)}{log(0.4)}$ 至少需要拨打5次。所以配置的模块数量为$\lceil \frac{5\ast N}{4320\ast 10}\rceil$ ，设N=100000，则模块数为12个，机器人数为144个。

现实情况

用户第n次是否接听与前n-1次存在密切联系，且随着n的变大接听率也随着变大，即第二次的接听率大于第一次，假设用户的接听率随着拨打的次数按25%比例增加，即有：第一次p1=50%，第二次p2=75%，第三次p3=100%，第三次必定接听，设生成函数：
$f(x)=a\cdot x+b\cdot x^2+c\cdot x^3$
其中x的次方n代表第n次接听，x的系数为第n次接听的人数。则有：
$a=N\cdot P_1$
$b=(N-a)\cdot P_2$
$c=(N-(a+b))\cdot P_3$
则需要拨打的总数 $s=a+2\cdot b+3\cdot c$
一般情况：
设：

• $p_i为第i次接听率，i>0且有p_i<p_{(i+1)}$
• $f(x)={\omega }_{1}x+{\omega }_2{x}^2+\cdots +{\omega }_i{x}^i为N通电话被接听的生成函数，参数含义同上$
  则有：
  ${\omega }_1=N\cdot p_1$
  ${\omega }_2=(N-{\omega }_1)\cdot p_2$
  …
  ${\omega }_i=(N-{\sum }_{j=1}^{i-1}{\omega }_j)\ast p_i$

则有：$s={\sum }_{i=1}^{N}i\cdot {\omega }_i=N\cdot p_1+{\sum }_{i=2}^{N}i\cdot (N-{\sum }_{j=1}^{i-1}{\omega }_j)\cdot p_i$

设P={50%，75%，100%},N=100000带入，得：$s=50000+2\cdot 37500+3\cdot 12500=162500$
所以配置的模块数量为$\lceil \frac{162500}{4320\ast 10}\rceil$，得模块数为4个，机器人数为48个。