本文深入探讨了FP-Growth算法，一种改进的关联规则挖掘算法，旨在解决Apriori算法的候选集问题和多次数据库访问问题。通过构建FP树，算法仅需两次访问数据库即可挖掘出所有频繁项集，显著提高了效率。
频繁模式增长Frequent-Pattern Growth（FP-Growth）
由于Apriori算法的两大缺陷：
- 大量候选集问题
- 多次访问数据库
FP-Growth特点：
- 将代表频繁项集的数据库压缩成一棵频繁模式树
- 无候选集
- 只需两次访问数据库
从DB构建一个FP树
- 扫描DB，导出 频繁项集（1-项集）
- 将频繁项降序排列 ，创建出 项头表
- 再次扫描DB，构建FP树
事务信息表
| TID | Item bought | frequent items（由大到小） |
|---|---|---|
| 100 | { f , a , c , d , g , i , m , p } | { f , c , a , m , p} |
| 200 | { a , b , c , f , m , o } | { f ,c , a , m , p} |
| 300 | { b , f , h , j , o } | { f , b } |
| 400 | { b , c , k , s , p} | { c , b , p} |
| 500 | { a , f , c , e , l , p , m , n } | { f , c , a , m , p } |
最小支持度min_support | 0.5 |
项头表
| Item | frequency（降序） | head |
|---|---|---|
| f | 4 | |
| c | 4 | |
| a | 3 | |
| b | 3 | |
| m | 3 | |
| p | 3 |
构造过程
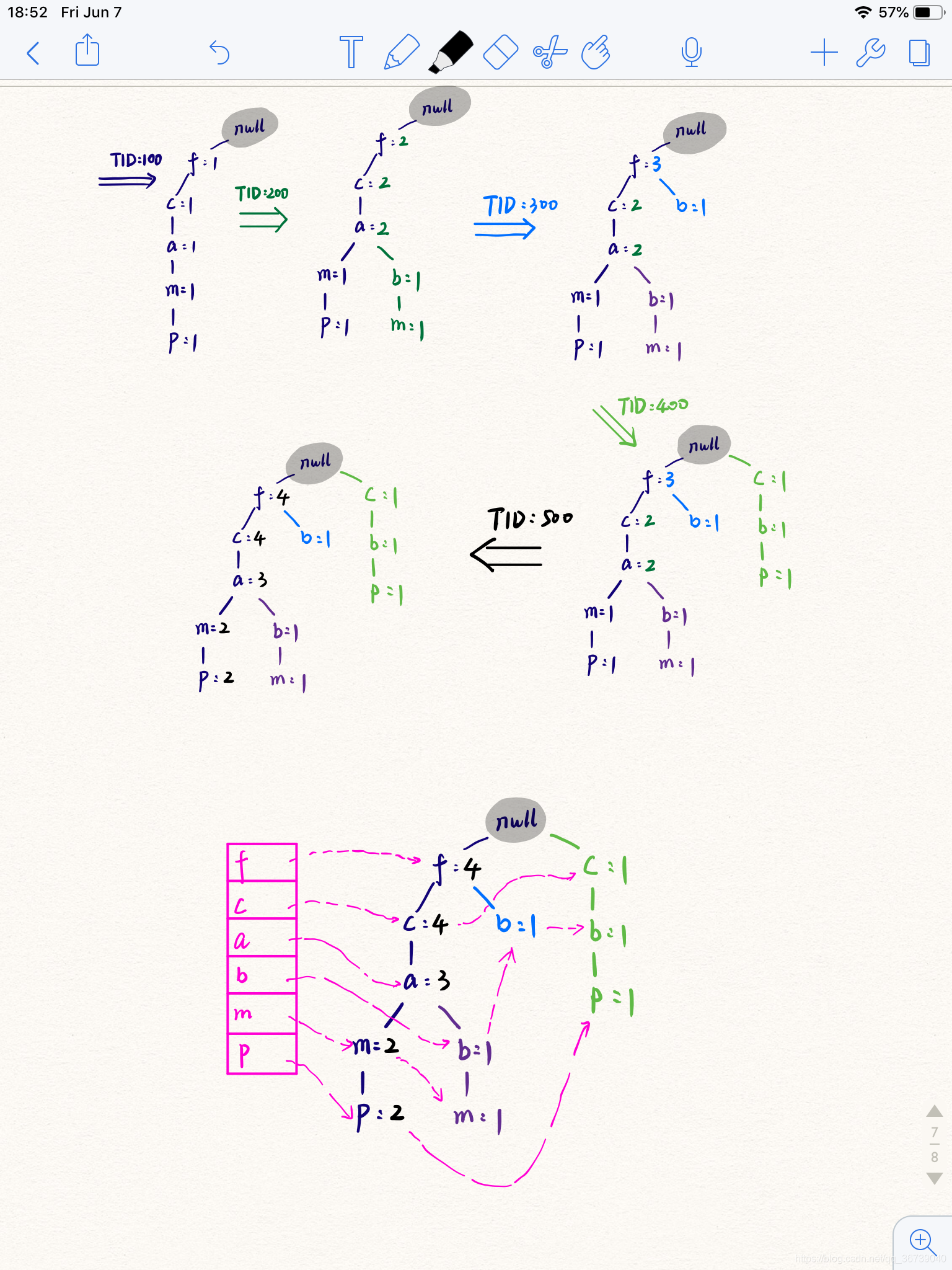
挖掘FP树
mining：
- 项头表由底到顶挖掘
- 获取条件模式基（一个FP子树）
步骤Step ： 设阀值为 2
| step | operate（behavior） | Example |
|---|---|---|
| 1 | 找到FP树的一个叶子结点 X | X=b |
| 2 | 对 X 所有的祖先节点计数 | （ f：2，c：1，a：1，b：2） |
| 3 | 删除低于阀值的计数 | （ f：2，b：2 ） |
| 4 | 可得到频繁K项集（K值为满足阀值节点数目） | （ f：2，b：2 ） |
| 5 | 满足阀值节点的组合就是频繁项集 （1-项集可直接得到） | { f，b} |
| step | Example |
|---|---|
| 1 | X=m |
| 2 | f：3，c：3，a：3，m：3，b：1 |
| 3 | f：3，c：3，a：3，m：3 |
| 4 | （ f：3，c：3，a：3，m：3 ） |
| 5 | { f ， m } ，{ c，m } ，{ a，m } ，{ f，c，m } ，{ f，a，m }，{ c，a，m }，{ f，c，a，m } |
FP-Growth构建
# -*- coding: utf-8 -*-
"""
Created on Sat Jun 8 11:22:00 2019
@author: ALVIN
"""
''' python基础知识
sorted()函数
：是一个高阶函数，它还可以接收一个key函数来实现自定义的排序
：例如按绝对值大小排序：sorted([36, 5, -12, 9, -21], key=abs)
：要进行反向排序，不必改动key函数，可以传入第三个参数reverse=True 。
：sorted(list, key=abs,reverse=True)
lambda表达式
lambda 参数列表：表达式
lambda parm1,parm2,...,parmn : expression
lambda p:p[1],reverse = True
'''
from numpy import *
class treeNode:
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue #结点名称
self.count = numOccur #节点计数值
self.nodeLink = None #用于链接相似的元素项
self.parent = parentNode #needs to be updated
self.children = {} #子节点
def inc(self,numOccur): #增加count数目
self.count += numOccur
def disp(self,ind = 1):
print(' '*ind,self.name,' ',self.count)
for child in self.children.values():
child.disp(ind+1)
'''**********************************FP构建*************************************'''
#FP构建函数
#dataSet 事务集合 其中每一条都是一项事务（比如购买：小米耳机、华为手机、Ipad）
def createTree(dataSet,minSup = 1):
#==============================项头表的构建===================================
#项头表 事务中每一个项 出现的次数
# {} 是python的集合类型也可以是字典（这儿是字典）
#---------------------项头表的构建（包含所有的项）------------------------------
headerTable = {}
for trans in dataSet:#trans 是一个事务
for item in trans: #item 是事务中的单个项
#记录每个元素项出现的频度
headerTable[item] = headerTable.get(item,0) + dataSet[trans]
''' headerTable是key-value的形式：如下
h 1
r 3
z 5
'''
#---------------------项头表的构建（删除不符合的项）----------------------------
#!!字典迭代时候不能修改、删除
for key in list(headerTable.keys()):
if headerTable[key] < minSup:
#将不满足最小支持度的删掉
del(headerTable[key])
#将项头表的所有项 放入集合
freqItemSet = set(headerTable.keys())
#判断是否存在满足最小支持度要求的（若没有则没有意义了）
if len(freqItemSet) == 0:#不满足最小值支持度要求的除去
return None,None
#设置项投表标准格式 ：由1到2
# 1. key项 - value（出现次数 ）
# 2. key项 - value（出现次数 - 指向）
for key in headerTable:
headerTable[key] = [headerTable[key],None]
#=====================项头表的构建完成=========================================
#=====================FP树的构建==============================================
retTree = treeNode('Null Set',1,None)
#每次循环就会将一个事务的数据写入到FP-Growth树中
#for循环多参数时候 in后的数据的一般需要 使用zip(data)
#dataSet是字典类型 字典类型可以直接使用for循环的多参数方式
for tranSet,count in dataSet.items():
# test用 print(tranSet,count)
# 打印结果：frozenset({'h', 'r', 'z', 'p', 'j'}) 1 ....
localD = {}
for item in tranSet:
#判断item是否在频繁项集中
if item in freqItemSet:
#将每条事务中满足min_support的项用key-value的方式取出放入localD中
localD[item] = headerTable[item][0]
if len(localD) > 0:
#将localD用出现次数(value)排序 并且放到 orderedItems之中
orderedItems = [v[0] for v in sorted(localD.items(),key = lambda p:p[1],reverse = True)]
#将排序后的item集合填充的树中
updateTree(orderedItems,retTree,headerTable,count)
#返回树型结构和头指针表
return retTree,headerTable
#=====================FP树的构建完成==============================================
#将排序后的item集合填充的树中（递归的方式）
#item 是满足min_support并且 使用频繁数目由大到小排序的 项 列表 如：['x', 'r', 's']
#inTree 是FP-Growth树的根
#headerTable 是项头表
#count是 ？？？ （感觉没什么必要）
def updateTree(items, inTree, headerTable, count):
#判断第一个结点是否是null的子节点 就是说该节点已经存入
if items[0] in inTree.children:
#是 则该结点count加 1
inTree.children[items[0]].inc(count)
else:
#创建一个结点 并设置为 Null 结点的子节点
inTree.children[items[0]] = treeNode(items[0], count, inTree)
#判断项头表的指向 是否已经设置
if headerTable[items[0]][1] == None:
#未设置则项头表的指向 设置为该节点
headerTable[items[0]][1] = inTree.children[items[0]]
else:
#已设置则项头表的指向 添加到项头表的指向链的链尾
#items[0] --> key headerTable[key] --> (value,linkNode)
#headerTable[key][0] 代表值 headerTable[key][1] 代表指向
updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
#判断 items 中不止一个 项
if len(items) > 1:
#递归操作
updateTree(items[1::], inTree.children[items[0]], headerTable, count)
#更新项头表的指向链，链表的尾插法
def updateHeader(nodeToTest, targetNode):
while (nodeToTest.nodeLink != None):
nodeToTest = nodeToTest.nodeLink
nodeToTest.nodeLink = targetNode
#加载测试数据
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
#初始化事务集 使用字典的方式存储
def createInitSet(dataSet):
retDict = {}
for trans in dataSet:
retDict[frozenset(trans)] = 1
return retDict
'''**********************************FP树挖掘***********************************'''
#=====================抽取条件模式基=============================================
#迭代上溯整棵树 结合树来看：竖向）
#leafNode 开始向上迭代的叶子节点
#prefixPath 存储向上迭代路径节点的列表
def ascendTree(leafNode, prefixPath):
if leafNode.parent != None:
prefixPath.append(leafNode.name)
ascendTree(leafNode.parent, prefixPath)
#从项头表的指向开始 获取所有basePat的项的向上迭代的路径集合（结合树来看：横向）
#basePat 开始向上迭代的叶子节点
#treeNode 该节点对应项头表的指向
def findPrefixPath(basePat, treeNode): #treeNode comes from header table
condPats = {}
while treeNode != None:
prefixPath = []
#迭代上溯整棵树
ascendTree(treeNode, prefixPath)
if len(prefixPath) > 1:
#不算上叶子节点 所以使用[1： ]的方式
condPats[frozenset(prefixPath[1:])] = treeNode.count
treeNode = treeNode.nodeLink
#使用Key-Value的方式存储 路径集合 与 对应的叶子节点计数
return condPats
#=====================递归查找频繁项集===========================================
#inTree ：FP-Growth树
#headerTable：项头表 key（name）：value（Frequent num，pointer）
#minSup：最小支持度要求
#preFix：？？？？？？？？？？？？
#freqItemList：频繁项集列表
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
#将headerTable.items()的key用出现次数(value)排序 并且放到 bigL 之中 （由小到大）
# 1.排序头指针表
bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1][0])]
#print(bigL)
#从头指针表的底端开始
for basePat in bigL:
newFreqSet = preFix.copy()
newFreqSet.add(basePat)
#添加的频繁项列表
freqItemList.append(newFreqSet)
print ('finalFrequent Item: ',newFreqSet)
condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
print ('condPattBases :',basePat, condPattBases)
# 2.从条件模式基创建条件FP树
myCondTree, myHead = createTree(condPattBases, minSup)
# 3.挖掘条件FP树
if myHead != None:
mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
print ('\n\n')
'''********************************** test ***********************************'''
minSupport = 3
simpDat = loadSimpDat()
initSet = createInitSet(simpDat)
myFPtree,myHeaderTab = createTree(initSet,minSupport)
print('-----------------------FP树：')
a = myFPtree.disp()
print('-----------------------项头表：')
lis = [v[0] for v in sorted(myHeaderTab.items(), key=lambda p: p[1][0])]
for k in lis:
print(k,myHeaderTab[k][0])
print('-----------------------mining：')
myFreqList = []
mineTree(myFPtree, myHeaderTab, minSupport, set([]), myFreqList)
扫一扫
851
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
