朴素贝叶斯网络进行邮件分类

朴素贝叶斯网络进行邮件分类

将以前做的邮件分类做个总结！

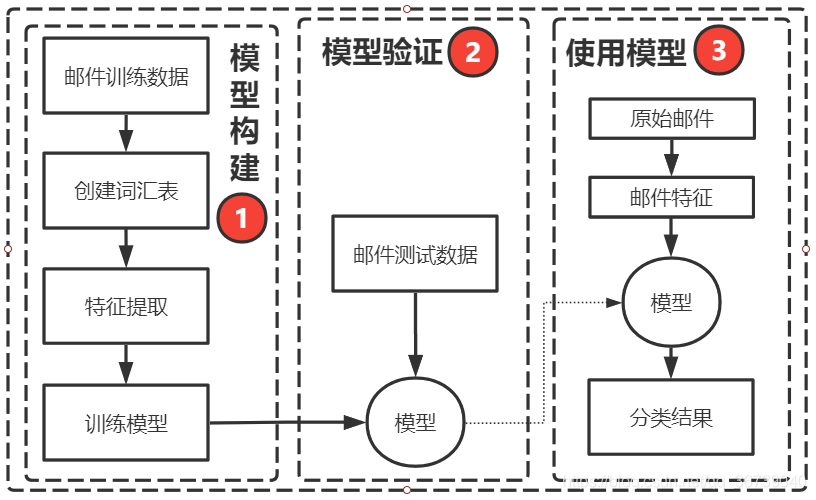
总体框架

下面我们将通过以下几个步骤，编写一个现实可用的垃圾邮件过滤器：

准备邮件数据；

创建词汇表；

特征提取；

训练模型；

模型验证；

使用模型。

分词与词汇表创建

删除可能是噪音的词

这一类词主要包括了副词、连词、语气助词、连词等，如常见的“在”、“的”、“而且”之类，其没有明确语义，对垃圾邮件过滤问题没有太大意义。

统一表示与词汇表

邮件体文本是不能被计算机所直接识别的，需要将其转换成计算机能够理解的形式；

一般形式是：[(‘您好’, 1) , (‘恭喜’, 0) , …, (‘谢谢’, 1) ]， 前者是出现的词，后者是在对应邮件是否出现。

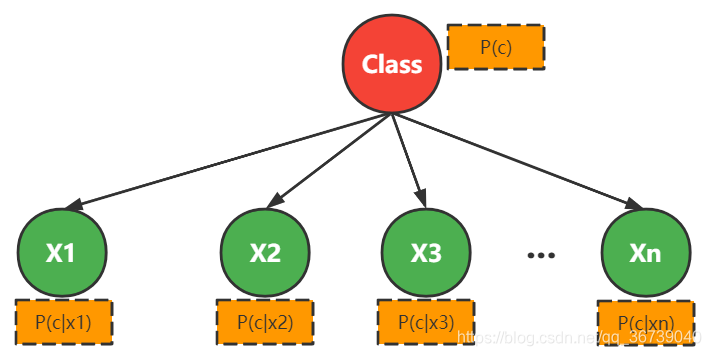
模型公式与其含义

样本： M封邮件，每份邮件被标记为垃圾邮件或者非垃圾邮件；

目标： 第 M+1封邮件来的时候，判断是否是垃圾邮件；

类别c： 垃圾邮件$c1$，非垃圾邮件$c2$

词汇表： 统计M封邮件中出现的所有单词，记单词数目为N，即形成词汇表。

将每个样本si向量化： 初始化N维向量$x_i$，若词$w_j$在$s_i$中出现，则$x_{ij}=1$，否则，为0。从而得到1000个$N$维向量$x$。
$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod _{i=1}^{N}P(x_i|c)$$

对于所有类别来说，$P(x)$ 的值是一致的，所以使用一般直接计算：
$$c=argma{x}_{c_i\in C}P(c_i)\prod _{i=1}^{N}P(x_i|c)$$
$$P(c|x_i)=ma{x}_{c_i\in C}P(c_i)\prod _{i=1}^{N}P(x_i|c)$$
具有最大概率的作为 样本 $x_i$ 的类别
$$P(c_i)=\frac{|D_{c_i}|+1}{|D|+C_i}$$
$$P(x_i|c_i)=\frac{|D_{c_i,x_i}|+1}{|D_{c_i}|+S_i}$$

$|D|$：样本总数目（在这儿就是邮件数目）
$|D_{c_i}|$：第 i 个类别的样本数目Or 类别为$c_i$的样本数目（比如：垃圾邮件的数目，正常邮件的数目）
$|D_{c_i,x_i}|$：属性值为$x_i$ ，类别为$c_i$的样本数目
$C$：数据集中可能的决策属性（类属性）。（比如：邮件分类是个二分类任务，这儿就是 {0,1}）
$C_n$：数据集中可能的决策属性（类属性）的取值数目。（比如：邮件分类是个二分类任务，这儿的取值就是 2 了）
$S_i$：第 i 个属性可能的取值数，比如：某个词（属性）存在则取值1，不存在则为0，所以该属性的取值为[0, 1]

遇到生词怎么办？

$+1$ 的目的是进行平滑（常常使用拉普拉斯修正）：这是由于 $|D_{c_i}|$ 或者 $|D_{x_i,c_i}|$ 的取值可能为 0，而计算的时候是累积 $\prod$ 计算。

如何判定该分类器的正确率？

交叉验证

相关资料

机器学习项目：构建垃圾邮件分类

文本分类：垃圾邮件分类

中文垃圾邮件分类

贝叶斯垃圾邮件分类