堆排序详解（C#）

堆

要使用堆排序，那我们首先要了解堆这个数据结构是怎么构建的，这样才能很好地使用堆排序。堆逻辑结构是完全二叉树，存储结构是顺序数组（存储结构是指写代码的时候保存堆中元素的数据结构）。堆分为最大堆和最小堆，最大堆指所有根节点大于左右孩子节点的值，最小堆相反，指所有根节点小于左右孩子节点的值，本文以最大堆为例介绍堆。

完全二叉树

上述提到堆的逻辑结构是完全二叉树，那这里就简单介绍下和堆相关的完全二叉树的特点：

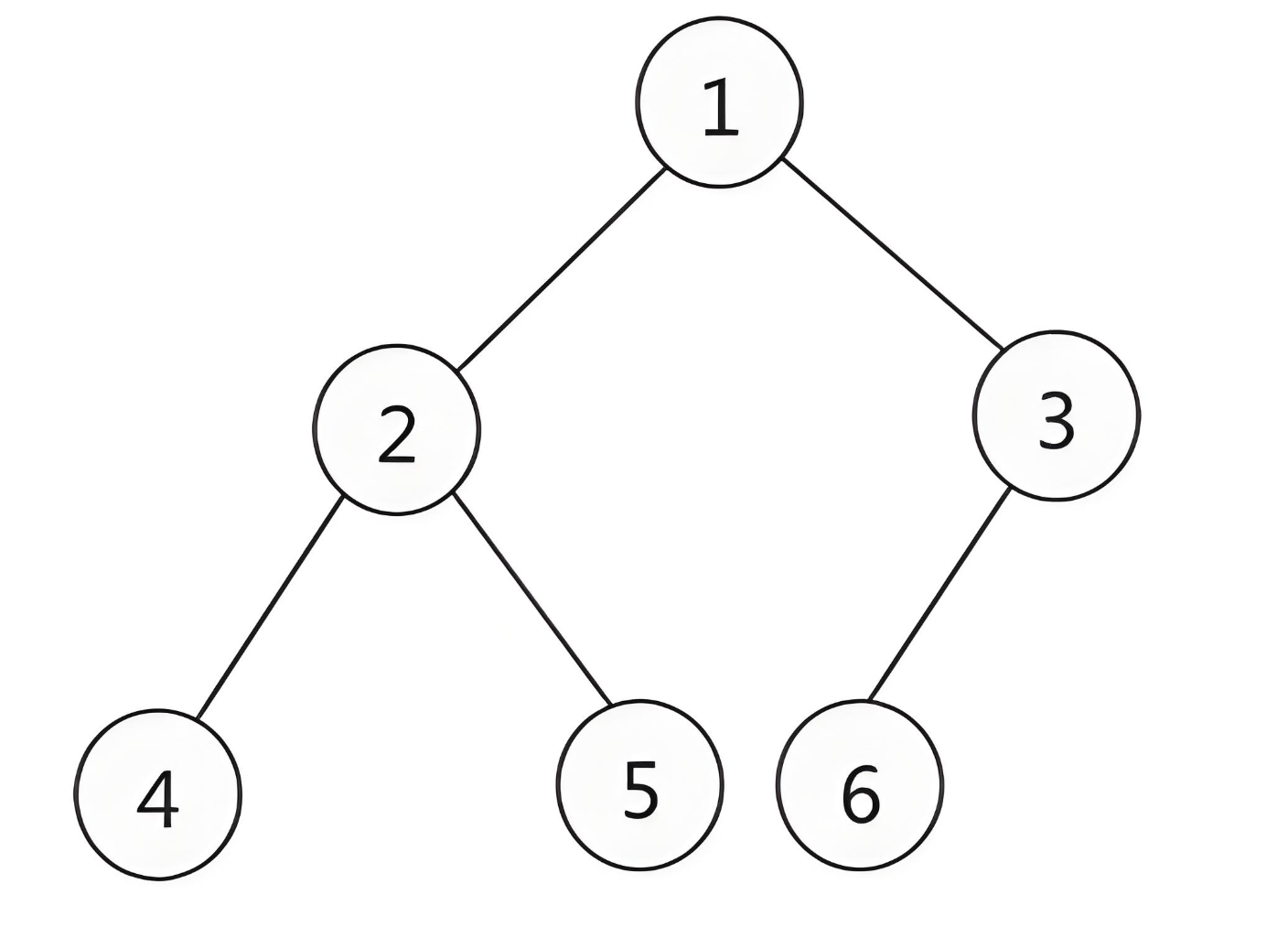
如图所示：

1. 完全二叉树的编号从1开始，按照层次遍历的顺序进行后续节点的编号。
2. 除了叶子节点外，所有的根节点都具备左右孩子。
3. 最后一层的叶子节点必须是连续的，以上图举例，意思是必须是4 -> 5 -> 6 三个叶子节点挨着排列，假设编号为6的节点是编号为3的节点的右孩子，那中间就空出了一个位置，就不符合连续的特点了。
4. 节点编号关系：左孩子节点编号 = 根节点编号 * 2，右孩子节点编号 = 根节点编号 * 2 + 1。（方便我们通过根节点索引去找到左右孩子节点索引）

正是这样的结构方便我们使用顺序数组进行存储，如下图所示：

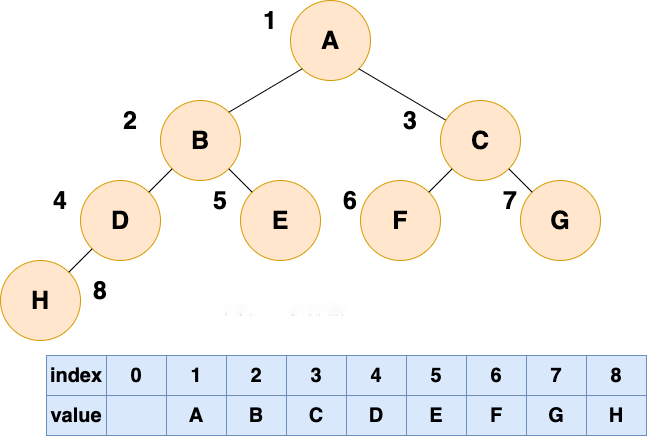
这样我们就把逻辑结构转化为了顺序数组，在后续构建堆的过程中我们只需要对这个顺序数组进行操作就行了。

建堆

堆就是在完全二叉树的基础上，增加了根节点与左右孩子节点的大小关系的数据结构。
以最大堆举例，其特点就是所有根节点的值大于所有左右孩子节点的值，我们需要依据这个特性去构建整个堆，建堆的过程大概分为如下两步：

1. 将原数组转化为上图提到的顺序存储结构（元素从索引1开始存放，索引0不存放数据）
2. 从下至上，从右至左，使所有的子树都具备最大堆的结构，那遍历到最上方的时候，是不是整棵树都具备了最大堆的性质

准备工作

 int[] heap_nums; // 堆数组
 int[] nums; // 原数组
 int heap_nums_len; // 堆数组长度
 int last_nor_leaf_node_index;// 最后一个非叶节点索引

这里记录最后一个非叶节点索引的原因后续会说明。

顺序存储结构

把原数组转化为符合完全二叉树性质的顺序存储结构

public void SeqStore(int[] nums)
{
    int len = nums.Length;
    for (int i = 0; i < len; i++)
    {
        heap_nums[i + 1] = nums[i];
    }
}

建堆

按照上述提到的使所有子树都要具备最大堆的结构，那我们需要从数组的末尾开始遍历所有的节点，确保所有子树都具备堆结构，由于叶子节点为根节点的子树只有它自己一个节点，已经符合堆结构了，所以我们只用从最后一个非叶节点开始遍历就好了。
在遍历每一个节点的时候，我们都要比较根节点和左右孩子节点的值是不是符合堆的特性，如果根节点比左右孩子小的话，那我们要把根节点的值和左右孩子节点中更大的那个值进行交换，使其符合堆的特性。
假设我们把根节点和其左右孩子节点中的其中一个进行了交换，那和根节点交换的那个节点的值就变为了根节点的值，交换了的这个节点的子树不一定还会满足堆的特性，这个时候我们还要接着检查交换之后是否满足堆结构的特性，直到满足堆结构的特性或是其变成了叶子节点，这个操作叫做下沉。
可参考视频：堆排序视频解析
下沉：下沉的时候要注意最后一个非叶节点右孩子可能不存在，要判断是否存在。

// 下沉，用于把堆中交换过后的值放到正确的位置
// 第二个参数用于堆排序
private void FallDown(int index, int heap_len)
{
    last_nor_leaf_node_index = (heap_len - 1) / 2;
    // 结束条件为其大于其左右孩子节点或是处于叶子结点
    while (index <= last_nor_leaf_node_index)
    {
        int left_index = 2 * index;
        int right_index = 2 * index + 1;
        
        int left_val = heap_nums[left_index];
        // 判断是否有右孩子, 没有就让他比根节点小就好了，这样后面做判断的时候就可以当他不存在
        int right_val = right_index < heap_len ? heap_nums[right_index] : heap_nums[index] - 1;
        // 如果大于左右孩子那直接结束, 注意越界问题，最后一个非叶节点不一定有右孩子
        if (heap_nums[index] > left_val && heap_nums[index] > right_val)
        {
            break;
        }

        // 三个中最大数的索引
        int max_index = left_val > right_val ? left_index : right_index;
        // 交换，更新index
        CommonFunc.Swap(ref heap_nums[max_index], ref heap_nums[index]);
        index = max_index;
    }
}

建堆：

// 建堆，这里默认最大堆
// 从最末尾的非叶子结点开始
public void Build()
{
    // 开始建堆
    for (int i = last_nor_leaf_node_index;i > 0;i--)
    {
        // 找到左右孩子的序号
        int left_index = 2 * i;
        int right_index = 2 * i + 1;

        int left_val = heap_nums[left_index];
        // 判断是否有右孩子, 没有就让他比根节点值小就好了，这样后面做判断的时候就可以当他不存在
        int right_val = right_index < heap_nums_len ? heap_nums[right_index] : heap_nums[i] - 1;

        // 小于左右孩子就要发生交换那就需要下沉
        // 注意右孩子可能不存在，要判断下越界问题
        if (heap_nums[i] < left_val || heap_nums[i] < right_val)
        {
            this.FallDown(i, heap_nums_len);
        }
    }
    Update();
}

堆排序

建好后的最大堆具备一个特点，最上面的根节点，也就是堆顶的值是整棵树的值最大的，那我们不是每次都提取堆顶的值，然后把这个值排除出堆，然后再用剩余的值重建一个堆，再提取堆顶的值，循环往复不就能获得一个递增的数组了？
我们选择把堆顶的值和数组最后一个值进行交换（处理起来更加方便），然后把最后一个值排除在外（逻辑上缩小数组的长度），然后把交换到堆顶的值做下沉操作不就完事儿了？

// 堆排序
public void Sort()
{
    // 建堆
    Build();
    // 从最末尾开始，和堆顶元素交换，这样最后一个元素就是整个数组最大的值
    for (int i = heap_nums_len - 1;i > 0;i--)
    {
        // 交换
        CommonFunc.Swap(ref heap_nums[1], ref heap_nums[i]);
        // 交换完之后不一定还符合堆结构，下沉,这时要排除最后一个元素
        FallDown(1, (i-1) + 1);
    }
    // 更新原数组
    Update();
}

// 更新原数组的值
public void Update()
{
    for (int i = 1;i < heap_nums_len;i++)
    {
        nums[i-1] = heap_nums[i];
    }
}

以上就是堆排序的所有内容了，可以结合视频更方便理解整个过程。